11.2: Potentiometric Methods
- Page ID
- 220756
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In potentiometry we measure the potential of an electrochemical cell under static conditions. Because no current—or only a negligible current—flows through the electrochemical cell, its composition remains unchanged. For this reason, potentiometry is a useful quantitative method of analysis. The first quantitative potentiometric applications appeared soon after the formulation, in 1889, of the Nernst equation, which relates an electrochemical cell’s potential to the concentration of electroactive species in the cell [Stork, J. T. Anal. Chem. 1993, 65, 344A–351A].
For an on-line introduction to much of the material in this section, see Analytical Electrochemistry: Potentiometry by Erin Gross, Richard S. Kelly, and Donald M. Cannon, Jr., a resource that is part of the Analytical Sciences Digital Library.
Potentiometry initially was restricted to redox equilibria at metallic electrodes, which limited its application to a few ions. In 1906, Cremer discovered that the potential difference across a thin glass membrane is a function of pH when opposite sides of the membrane are in contact with solutions that have different concentrations of H3O+. This discovery led to the development of the glass pH electrode in 1909. Other types of membranes also yield useful potentials. For example, in 1937 Kolthoff and Sanders showed that a pellet of AgCl can be used to determine the concentration of Ag+. Electrodes based on membrane potentials are called ion-selective electrodes, and their continued development extends potentiometry to a diverse array of analytes.
Potentiometric Measurements
As shown in Figure 11.1.3, we use a potentiometer to determine the difference between the potential of two electrodes. The potential of one electrode—the working or indicator electrode—responds to the analyte’s activity and the other electrode—the counter or reference electrode—has a known, fixed potential. In this section we introduce the conventions for describing potentiometric electrochemical cells, and the relationship between the measured potential and the analyte’s activity.
In Chapter 6 we noted that a chemical reaction’s equilibrium position is a function of the activities of the reactants and products, not their concentrations. To be correct, we should write the Nernst equation in terms of activities. So why didn’t we use activities in Chapter 9 when we calculated redox titration curves? There are two reasons for that choice. First, concentrations are always easier to calculate than activities. Second, in a redox titration we determine the analyte’s concentration from the titration’s end point, not from the potential at the end point. The only reasons for calculating a titration curve is to evaluate its feasibility and to help us select a useful indicator. In most cases, the error we introduce by assuming that concentration and activity are identical is too small to be a significant concern.
In potentiometry we cannot ignore the difference between activity and concentration. Later in this section we will consider how we can design a potentiometric method so that we can ignore the difference between activity and concentration. See Chapter 6.9 to review our earlier discussion of activity and concentration.
Potentiometric Electrochemical Cells
A schematic diagram of a typical potentiometric electrochemical cell is shown in Figure \(\PageIndex{1}\). The electrochemical cell consists of two half-cells, each of which contains an electrode immersed in a solution of ions whose activities determine the electrode’s potential. A salt bridge that contains an inert electrolyte, such as KCl, connects the two half-cells. The ends of the salt bridge are fixed with porous frits, which allow the electrolyte’s ions to move freely between the half-cells and the salt bridge. This movement of ions in the salt bridge completes the electrical circuit.
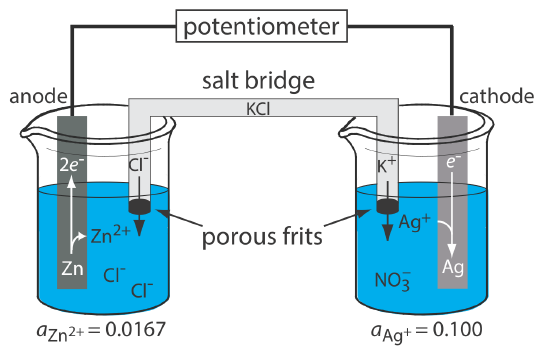
By convention, we identify the electrode on the left as the anode and assign to it the oxidation reaction; thus
\[\mathrm{Zn}(s) \rightleftharpoons \text{ Zn}^{2+}(a q)+2 e^{-} \nonumber\]
The electrode on the right is the cathode, where the reduction reaction occurs.
\[\mathrm{Ag}^{+}(a q)+e^{-} \rightleftharpoons \mathrm{Ag}(s) \nonumber\]
The potential of the electrochemical cell in Figure \(\PageIndex{1}\) is for the reaction
\[\mathrm{Zn}(s)+2 \mathrm{Ag}^{+}(a q) \rightleftharpoons 2 \mathrm{Ag}(s)+\mathrm{Zn}^{2+}(\mathrm{aq}) \nonumber\]
We also define potentiometric electrochemical cells such that the cathode is the indicator electrode and the anode is the reference electrode.
The reason for separating the electrodes is to prevent the oxidation reaction and the reduction reaction from occurring at one of the electrodes. For example, if we place a strip of Zn metal in a solution of AgNO3, the reduction of Ag+ to Ag occurs on the surface of the Zn at the same time as a potion of the Zn metal oxidizes to Zn2+. Because the transfer of electrons from Zn to Ag+ occurs at the electrode’s surface, we can not pass them through the potentiometer.
Shorthand Notation for Electrochemical Cells
Although Figure \(\PageIndex{1}\) provides a useful picture of an electrochemical cell, it is not a convenient way to represent it (Imagine having to draw a picture of each electrochemical cell you are using!). A more useful way to describe an electrochemical cell is a shorthand notation that uses symbols to identify different phases and that lists the composition of each phase. We use a vertical slash (|) to identify a boundary between two phases where a potential develops, and a comma (,) to separate species in the same phase or to identify a boundary between two phases where no potential develops. Shorthand cell notations begin with the anode and continue to the cathode. For example, we describe the electrochemical cell in Figure \(\PageIndex{1}\) using the following shorthand notation.
\[\text{Zn}(s) | \text{ZnCl}_2(aq, a_{\text{Zn}^{2+}} = 0.0167) || \text{AgNO}_3(aq, a_{\text{Ag}^+} = 0.100) | \text{Ag} (s) \nonumber\]
The double vertical slash (||) represents the salt bridge, the contents of which we usually do not list. Note that a double vertical slash implies that there is a potential difference between the salt bridge and each half-cell.
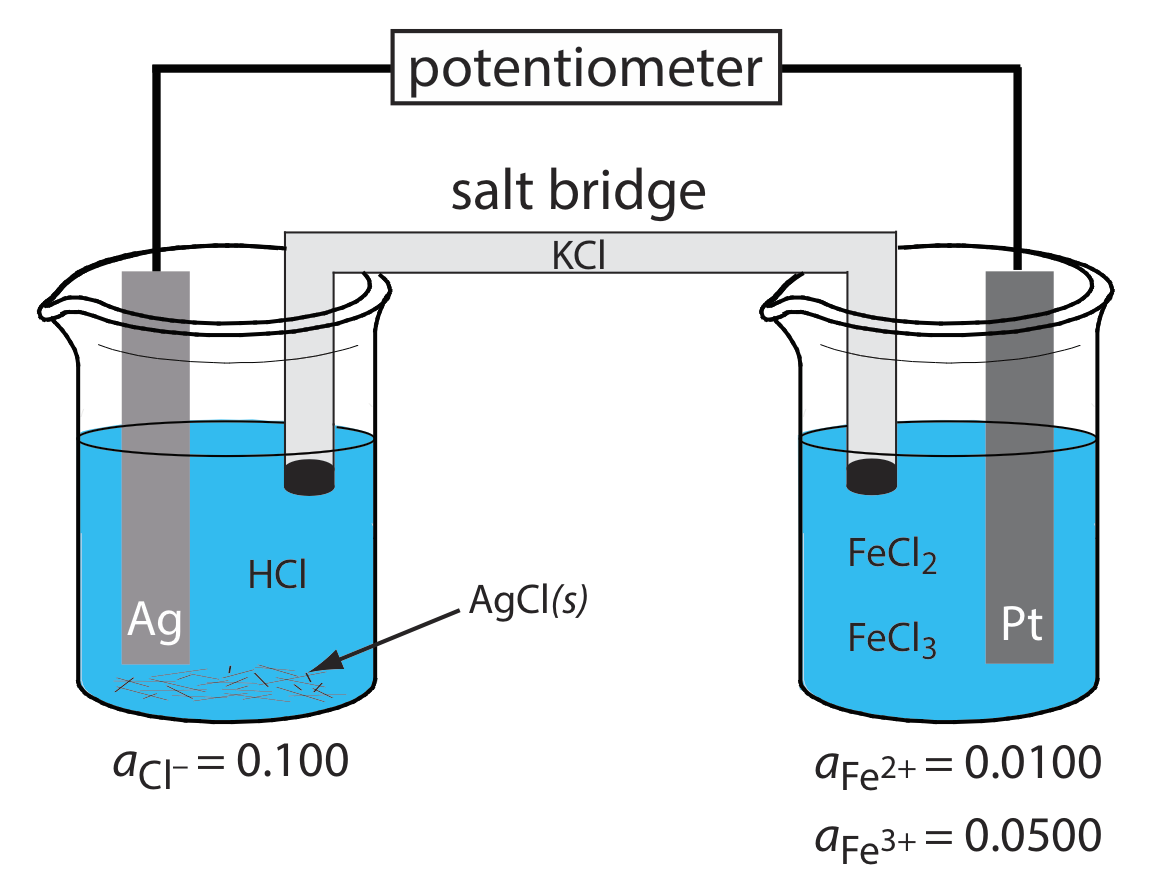
What are the anodic, the cathodic, and the overall reactions responsible for the potential of the electrochemical cell in Figure \(\PageIndex{2}\)? Write the shorthand notation for the electrochemical cell.
Solution
The oxidation of Ag to Ag+ occurs at the anode, which is the left half-cell. Because the solution contains a source of Cl–, the anodic reaction is
\[\mathrm{Ag}(s)+\mathrm{Cl}^{-}(aq) \rightleftharpoons\text{ AgCl}(s)+e^{-} \nonumber\]
The cathodic reaction, which is the right half-cell, is the reduction of Fe3+ to Fe2+.
\[\mathrm{Fe}^{3+}(a q)+e^{-}\rightleftharpoons \text{ Fe}^{2+}(a q) \nonumber\]
The overall cell reaction, therefore, is
\[\mathrm{Ag}(s)+\text{ Fe}^{3+}(a q)+\text{ Cl}^{-}(a q) \rightleftharpoons \mathrm{AgCl}(s)+\text{ Fe}^{2+}(a q) \nonumber\]
The electrochemical cell’s shorthand notation is
\[\text{Ag}(s) | \text{HCl} (aq, a_{\text{Cl}^{-}} = 0.100), \text{AgCl} (\text{sat’d}) || \text{FeCl}_2(aq, a_{\text{Fe}^{2+}} = 0.0100), \text{ Fe}^{3+}(aq,a_{\text{Fe}^{3+}} = 0.0500) | \text{Pt} (s) \nonumber\]
Note that the Pt cathode is an inert electrode that carries electrons to the reduction half-reaction. The electrode itself does not undergo reduction.
Write the reactions occurring at the anode and the cathode for the potentiometric electrochemical cell with the following shorthand notation.
Pt(s) | H2(g), H+(aq) || Cu2+(aq) | Cu(s)
- Answer
-
The oxidation of H2 to H+ occurs at the anode
\[\mathrm{H}_{2}(g)\rightleftharpoons2 \mathrm{H}^{+}(a q)+2 e^{-} \nonumber\]
and the reduction of Cu2+ to Cu occurs at the cathode.
\[\mathrm{Cu}^{2+}(a q)+2 e^{-}\rightleftharpoons\mathrm{Cu}(s) \nonumber\]
The overall cell reaction, therefore, is
\[\mathrm{Cu}^{2+}(a q)+\text{ H}_{2}(g)\rightleftharpoons2 \mathrm{H}^{+}(a q)+\mathrm{Cu}(s) \nonumber\]
Potential and Activity—The Nernst Equation
The potential of a potentiometric electrochemical cell is
\[E_{\text {cell }}=E_{\text {cathode }}-E_{\text {anode }} \label{11.1}\]
where Ecathode and Eanode are reduction potentials for the redox reactions at the cathode and the anode, respectively. Each reduction potential is given by the Nernst equation
\[E=E^{\circ}-\frac{R T}{n F} \ln Q \nonumber\]
where Eo is the standard-state reduction potential, R is the gas constant, T is the temperature in Kelvins, n is the number of electrons in the redox reaction, F is Faraday’s constant, and Q is the reaction quotient. At a temperature of 298 K (25oC) the Nernst equation is
\[E=E^{\circ}-\frac{0.05916}{n} \log Q \label{11.2}\]
where E is in volts.
Using equation \ref{11.2}, the potential of the anode and cathode in Figure \(\PageIndex{1}\) are
\[E_\text{anode} = E_{\text{Zn}^{2+}/\text{Zn}}^{\circ} - \frac {0.05916} {2} \log \frac{1} {a_{\text{Zn}^{2+}}} \nonumber\]
\[E_\text{anode} = E_{\text{Ag}^{+}/\text{Ag}}^{\circ} - \frac {0.05916} {1} \log \frac{1} {a_{\text{Ag}^{+}}} \nonumber\]
Even though an oxidation reaction is taking place at the anode, we define the anode's potential in terms of the corresponding reduction reaction and the standard-state reduction potential. See Chapter 6.4 for a review of using the Nernst equation in calculations.
Substituting Ecathode and Eanode into equation \ref{11.1}, along with the activities of Zn2+ and Ag+ and the standard-state reduction potentials, gives Ecell as
\[E_\text{cell} = \left( E_{\text{Ag}^{+}/\text{Ag}}^{\circ} - \frac {0.05916} {1} \log \frac{1} {a_{\text{Ag}^{+}}} \right) - \left( E_{\text{Zn}^{2+}/\text{Zn}}^{\circ} - \frac {0.05916} {2} \log \frac{1} {a_{\text{Zn}^{2+}}} \right) \nonumber\]
\[E_\text{cell} = \left( 0.7996 - \frac {0.05916} {1} \log \frac{1} {0.100} \right) - \left( -0.7618 - \frac {0.05916} {2} \log \frac{1} {0.0167} \right) = 1.555 \text{ V} \nonumber\]
You will find values for the standard-state reduction potentials in Appendix 13.
What is the potential of the electrochemical cell shown in Example \(\PageIndex{1}\)?
Solution
Substituting Ecathode and Eanode into equation \ref{11.1}, along with the concentrations of Fe3+, Fe2+, and Cl– and the standard-state reduction potentials gives
\[E_\text{cell} = \left( E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} - \frac {0.05916} {1} \log \frac{a_{\text{Fe}^{2+}}} {a_{\text{Fe}^{3+}}} \right) - \left( E_{\text{AgCl/Ag}}^{\circ} - \frac {0.05916} {1} \log a_{\text{Cl}^-} \right) \nonumber\]
\[E_\text{cell} = \left( 0.771 - \frac {0.05916} {1} \log \frac{0.0100} {0.0500} \right) - \left( 0.2223 - \frac {0.05916} {1} \log (0.100) \right) = 0.531 \text{ V} \nonumber\]
What is the potential for the electrochemical cell in Exercise \(\PageIndex{1}\) if the activity of H+ in the anodic half-cell is 0.100, the fugacity of H2 in the anodic half-cell is 0.500, and the activity of Cu2+ in the cathodic half-cell is 0.0500? Fugacity, \(f\), is the equivalent term for the activity of a gas.
- Answer
-
Making appropriate substitutions into equation \ref{11.1} and solving for Ecell gives its value as
\[E_\text{cell} = \left( E_{\text{Cu}^{2+}/\text{Cu}}^{\circ} - \frac {0.05916} {2} \log \frac{1} {a_{\text{Cu}^{2+}}} \right) - \left( E_{\text{H}^{+}/\text{H}_2}^{\circ} - \frac {0.05916} {2} \log \frac{f_{\text{H}_2}} {a_{\text{H}^+}^2} \right) \nonumber\]
\[E_\text{cell} = \left( 0.3419 - \frac {0.05916} {2} \log \frac{1} {0.0500} \right) - \left( 0.0000 - \frac {0.05916} {2} \log \frac{0.500} {(0.100)^2} \right) = 0.3537 \text{ V} \nonumber\]
In potentiometry, we assign the reference electrode to the anodic half-cell and assign the indicator electrode to the cathodic half-cell. Thus, if the potential of the cell in Figure \(\PageIndex{1}\) is +1.50 V and the activity of Zn2+ is 0.0167, then we can solve the following equation for aAg+
\[1.50 \text{ V} = \left( 0.7996 - \frac {0.05916} {1} \log \frac{1} {a_{\text{Ag}^+}} \right) - \left( -0.7618 - \frac {0.05916} {2} \log \frac{1} {0.0167} \right) \nonumber\]
obtaining an activity of 0.0118.
What is the activity of Fe3+ in an electrochemical cell similar to that in Example \(\PageIndex{1}\) if the activity of Cl– in the left-hand cell is 1.0, the activity of Fe2+ in the right-hand cell is 0.015, and Ecell is +0.546 V?
Solution
Making appropriate substitutions into equation \ref{11.1}
\[0.546 = \left( 0.771 - \frac {0.05916} {1} \log \frac{0.0100} {a_{\text{Fe}^{3+}}} \right) - \left( 0.2223 - \frac {0.05916} {1} \log (1.0) \right) \nonumber\]
and solving for aFe3+ gives its activity as 0.0135.
What is the activity of Cu2+ in the electrochemical cell in Exercise \(\PageIndex{1}\) if the activity of H+ in the anodic half-cell is 1.00 with a fugacity of 1.00 for H2, and an Ecell of +0.257 V?
- Answer
-
Making appropriate substitutions into equation \ref{11.1}
\[0.257 \text{ V} = \left( 0.3419 - \frac {0.05916} {2} \log \frac{1} {a_{\text{Cu}^{2+}}} \right) - \left( 0.0000 - \frac {0.05916} {2} \log \frac{1.00} {(1.00)^2} \right) \nonumber\]
and solving for aCu2+ gives its activity as \(1.35 \times 10^{-3}\).
Despite the apparent ease of determining an analyte’s activity using the Nernst equation, there are several problems with this approach. One problem is that standard-state potentials are temperature-dependent and the values in reference tables usually are for a temperature of 25oC. We can overcome this problem by maintaining the electrochemical cell at 25oC or by measuring the standard-state potential at the desired temperature.
Another problem is that a standard-sate reduction potential may have a significant matrix effect. For example, the standard-state reduction potential for the Fe3+/Fe2+ redox couple is +0.735 V in 1 M HClO4, +0.70 V in 1 M HCl, and +0.53 V in 10 M HCl. The difference in potential for equimolar solutions of HCl and HClO4 is the result of a difference in the activity coefficients for Fe3+ and Fe2+ in these two media. The shift toward a more negative potential with an increase in the concentration of HCl is the result of chloride’s ability to form a stronger complex with Fe3+ than with Fe2+. We can minimize this problem by replacing the standard-state potential with a matrix-dependent formal potential. Most tables of standard-state potentials, including those in Appendix 13, include selected formal potentials.
Finally, a more serious problem is the presence of additional potentials in the electrochemical cell not included in equation \ref{11.1}. In writing the shorthand notation for an electrochemical cell we use a double slash (||) to indicate the salt bridge, suggesting a potential exists at the interface between each end of the salt bridge and the solution in which it is immersed. The origin of this potential is discussed in the following section.
Junction Potentials
A junction potential develops at the interface between two ionic solution if there is a difference in the concentration and mobility of the ions. Consider, for example, a porous membrane that separations a solution of 0.1 M HCl from a solution of 0.01 M HCl (Figure \(\PageIndex{3}\)a). Because the concentration of HCl on the membrane’s left side is greater than that on the right side of the membrane, H+ and Cl– will diffuse in the direction of the arrows. The mobility of H+, however, is greater than that for Cl–, as shown by the difference in the lengths of their respective arrows. Because of this difference in mobility, the solution on the right side of the membrane develops an excess concentration of H+ and a positive charge (Figure \(\PageIndex{3}\)b). Simultaneously, the solution on the membrane’s left side develops a negative charge because there is an excess concentration of Cl–. We call this difference in potential across the membrane a junction potential and represent it as Ej.
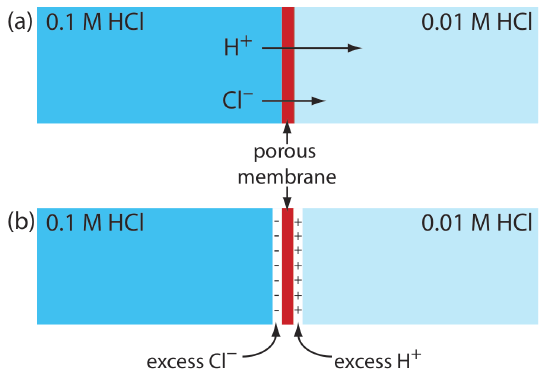
The magnitude of the junction potential depends upon the difference in the concentration of ions on the two sides of the interface, and may be as large as 30–40 mV. For example, a junction potential of 33.09 mV has been measured at the interface between solutions of 0.1 M HCl and 0.1 M NaCl [Sawyer, D. T.; Roberts, J. L., Jr. Experimental Electrochemistry for Chemists, Wiley-Interscience: New York, 1974, p. 22]. A salt bridge’s junction potential is minimized by using a salt, such as KCl, for which the mobilities of the cation and anion are approximately equal. We also can minimize the junction potential by incorporating a high concentration of the salt in the salt bridge. For this reason salt bridges frequently are constructed using solutions that are saturated with KCl. Nevertheless, a small junction potential, generally of unknown magnitude, is always present.
When we measure the potential of an electrochemical cell, the junction potential also contributes to Ecell; thus, we rewrite equation \ref{11.1} as
\[E_{\text {cell }}=E_{\text {cathode }}-E_{\text {anode }}+E_{j} \nonumber\]
to include its contribution. If we do not know the junction potential’s actual value—which is the usual situation—then we cannot directly calculate the analyte’s concentration using the Nernst equation. Quantitative analytical work is possible, however, if we use one of the standardization methods—external standards, the method of standard additions, or internal standards—discussed in Chapter 5.3.
Reference Electrodes
In a potentiometric electrochemical cell one of the two half-cells provides a fixed reference potential and the potential of the other half-cell responds the analyte’s concentration. By convention, the reference electrode is the anode; thus, the short hand notation for a potentiometric electrochemical cell is
reference electrode || indicator electrode
and the cell potential is
\[E_{\mathrm{cell}}=E_{\mathrm{ind}}-E_{\mathrm{ref}}+E_{j} \nonumber\]
The ideal reference electrode provides a stable, known potential so that we can attribute any change in Ecell to the analyte’s effect on the indicator electrode’s potential. In addition, it should be easy to make and to use the reference electrode. Three common reference electrodes are discussed in this section.
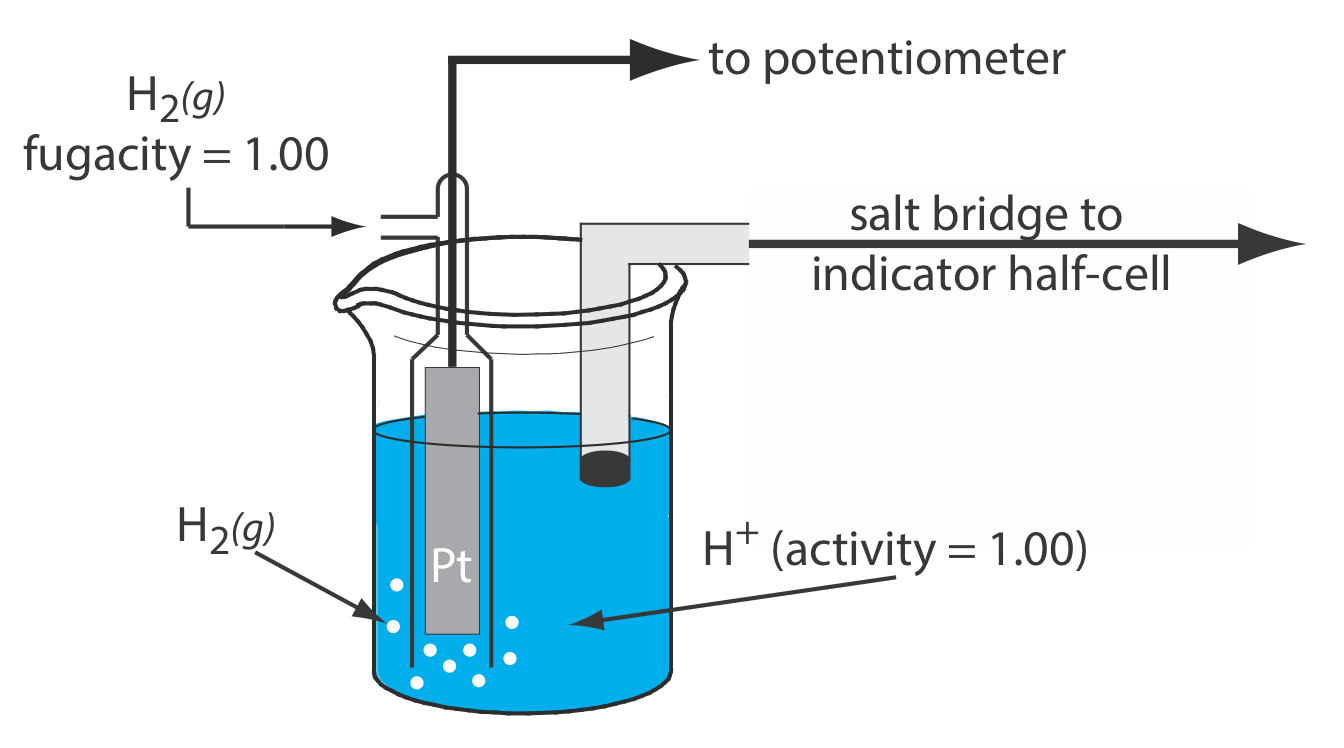
Standard Hydrogen Electrode
Although we rarely use the standard hydrogen electrode (SHE) for routine analytical work, it is the reference electrode used to establish standard-state potentials for other half-reactions. The SHE consists of a Pt electrode immersed in a solution in which the activity of hydrogen ion is 1.00 and in which the fugacity of H2(g) is 1.00 (Figure \(\PageIndex{4}\)). A conventional salt bridge connects the SHE to the indicator half-cell. The short hand notation for the standard hydrogen electrode is
\[\text{Pt}(s), \text{ H}_{2}\left(g, f_{\mathrm{H}_{2}}=1.00\right) | \text{ H}^{+}\left(a q, a_{\mathrm{H}^{+}}=1.00\right) \| \nonumber\]
and the standard-state potential for the reaction
\[\mathrm{H}^{+}(a q)+e^{-}=\frac{1}{2} \mathrm{H}_{2}(g) \nonumber\]
is, by definition, 0.00 V at all temperatures. Despite its importance as the fundamental reference electrode against which we measure all other potentials, the SHE is rarely used because it is difficult to prepare and inconvenient to use.
Calomel Electrodes
A calomel reference electrode is based on the following redox couple between Hg2Cl2 and Hg (calomel is the common name for Hg2Cl2)
\[\mathrm{Hg}_{2} \mathrm{Cl}_{2}(s)+2 e^{-}\rightleftharpoons2 \mathrm{Hg}(l)+2 \mathrm{Cl}^{-}(a q) \nonumber\]
for which the potential is
\[E=E_{\mathrm{Hg}_{2} \mathrm{Cl}_{2} / \mathrm{Hg}}^{\mathrm{o}}-\frac{0.05916}{2} \log \left(a_{\text{Cl}^-}\right)^{2}=+0.2682 \mathrm{V}-\frac{0.05916}{2} \log \left(a_{\text{Cl}^-}\right)^{2} \nonumber\]
The potential of a calomel electrode, therefore, depends on the activity of Cl– in equilibrium with Hg and Hg2Cl2.
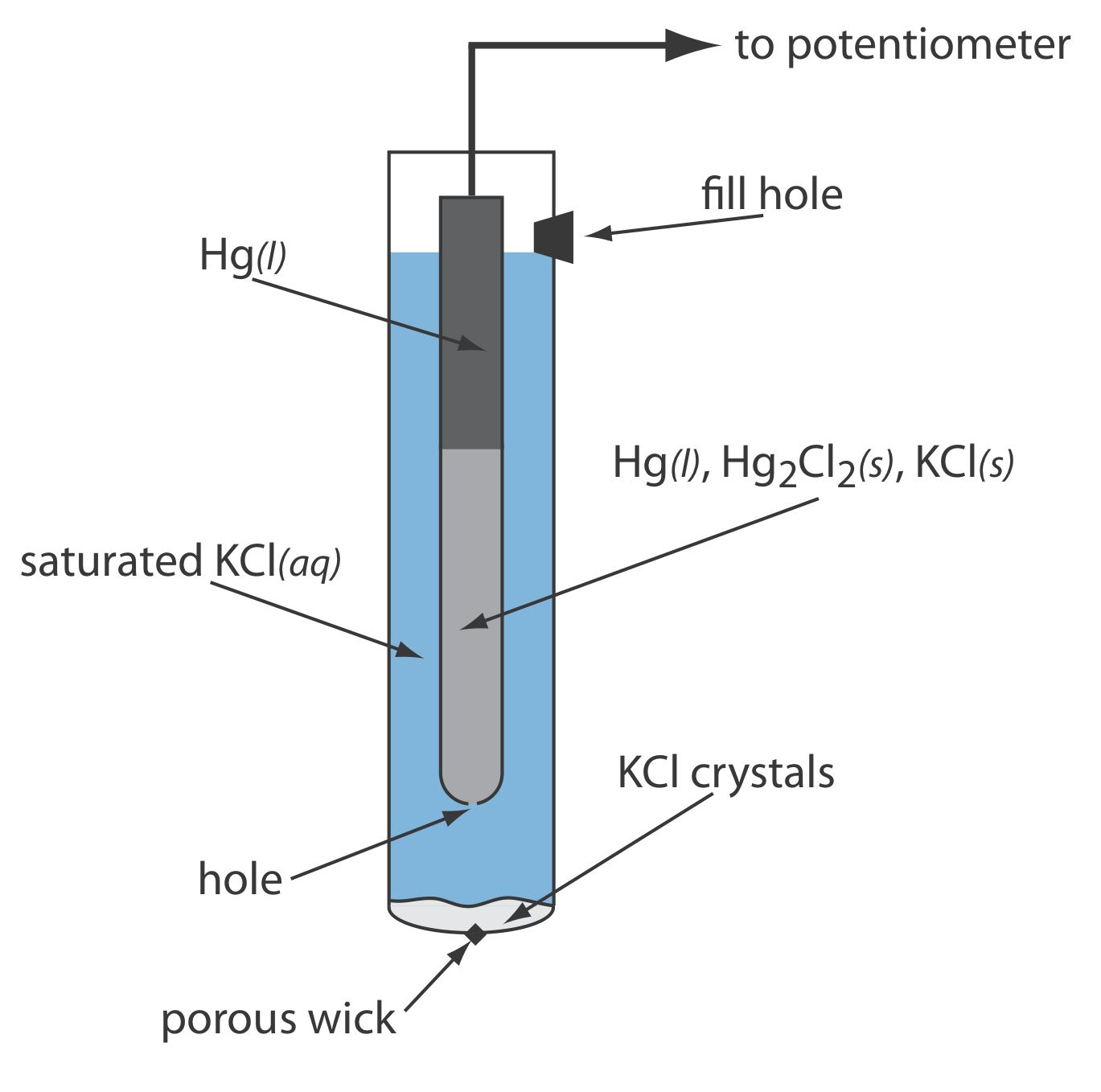
As shown in Figure \(\PageIndex{5}\), in a saturated calomel electrode (SCE) the concentration of Cl– is determined by the solubility of KCl. The electrode consists of an inner tube packed with a paste of Hg, Hg2Cl2, and KCl, situated within a second tube that contains a saturated solution of KCl. A small hole connects the two tubes and a porous wick serves as a salt bridge to the solution in which the SCE is immersed. A stopper in the outer tube provides an opening for adding addition saturated KCl. The short hand notation for this cell is
\[\mathrm{Hg}(l) | \mathrm{Hg}_{2} \mathrm{Cl}_{2}(s), \mathrm{KCl}(a q, \text { sat'd }) \| \nonumber\]
Because the concentration of Cl– is fixed by the solubility of KCl, the potential of an SCE remains constant even if we lose some of the inner solution to evaporation. A significant disadvantage of the SCE is that the solubility of KCl is sensitive to a change in temperature. At higher temperatures the solubility of KCl increases and the electrode’s potential decreases. For example, the potential of the SCE is +0.2444 V at 25oC and +0.2376 V at 35oC. The potential of a calomel electrode that contains an unsaturated solution of KCl is less dependent on the temperature, but its potential changes if the concentration, and thus the activity of Cl–, increases due to evaporation.
For example, the potential of a calomel electrode is +0.280 V when the concentration of KCl is 1.00 M and +0.336 V when the concentration of KCl is 0.100 M. If the activity of Cl– is 1.00, the potential is +0.2682 V.
Silver/Silver Chloride Electrodes
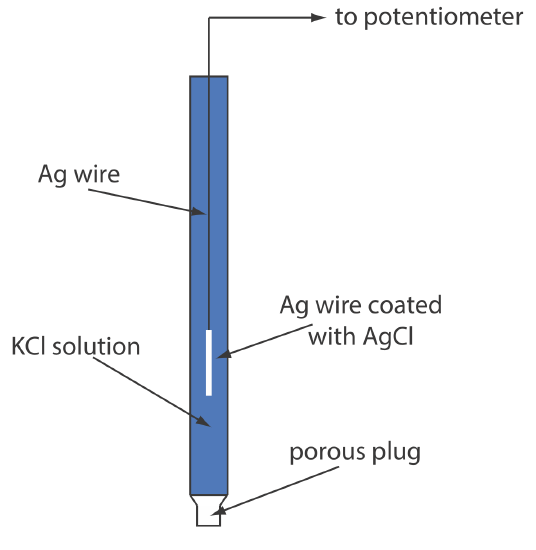
Another common reference electrode is the silver/silver chloride electrode, which is based on the reduction of AgCl to Ag.
\[\operatorname{AgCl}(s)+e^{-} \rightleftharpoons \mathrm{Ag}(s)+\mathrm{Cl}^{-}(a q) \nonumber\]
As is the case for the calomel electrode, the activity of Cl– determines the potential of the Ag/AgCl electrode; thus
\[E = E_\text{AgCl/Ag}^{\circ}-0.05916 \log a_{\text{Cl}^-} = 0.2223 \text{ V} - 0.05916 \log a_{\text{Cl}^-} \nonumber\]
When prepared using a saturated solution of KCl, the electrode's potential is +0.197 V at 25oC. Another common Ag/AgCl electrode uses a solution of 3.5 M KCl and has a potential of +0.205 V at 25oC. As you might expect, the potential of a Ag/AgCl electrode using a saturated solution of KCl is more sensitive to a change in temperature than an electrode that uses an unsaturated solution of KCl.
A typical Ag/AgCl electrode is shown in Figure \(\PageIndex{6}\) and consists of a silver wire, the end of which is coated with a thin film of AgCl, immersed in a solution that contains the desired concentration of KCl. A porous plug serves as the salt bridge. The electrode’s short hand notation is
\[\operatorname{Ag}(s) | \operatorname{Ag} \mathrm{Cl}(s), \mathrm{KCl}\left(a q, a_{\mathrm{Cl}^{-}}=x\right) \| \nonumber\]
Converting Potentials Between Reference Electrodes
The standard state reduction potentials in most tables are reported relative to the standard hydrogen electrode’s potential of +0.00 V. Because we rarely use the SHE as a reference electrode, we need to convert an indicator electrode’s potential to its equivalent value when using a different reference electrode. As shown in the following example, this is easy to do.
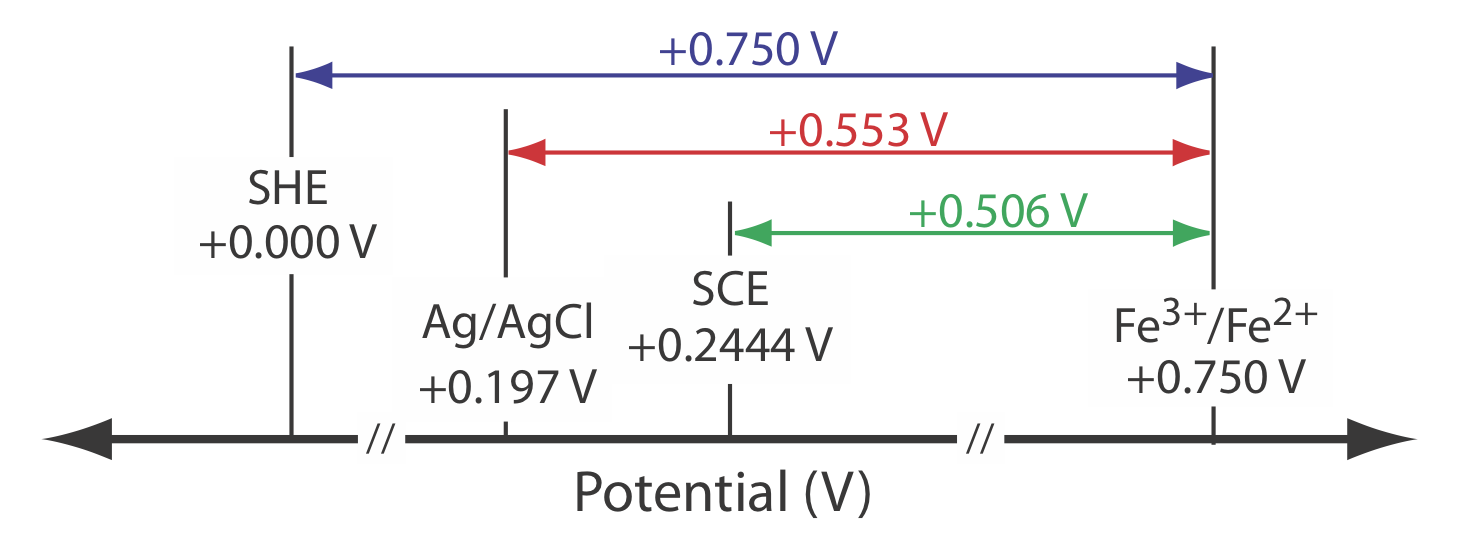
The potential for an Fe3+/Fe2+ half-cell is +0.750 V relative to the standard hydrogen electrode. What is its potential if we use a saturated calomel electrode or a saturated silver/silver chloride electrode?
Solution
When we use a standard hydrogen electrode the potential of the electrochemical cell is
\[E_\text{cell} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}} - E_\text{SHE} = 0.750 \text{ V} -0.000 \text{ V} = 0.750 \text{ V} \nonumber\]
We can use the same equation to calculate the potential if we use a saturated calomel electrode
\[E_\text{cell} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}} - E_\text{SHE} = 0.750 \text{ V} -0.2444 \text{ V} = 0.506 \text{ V} \nonumber\]
or a saturated silver/silver chloride electrode
\[E_\text{cell} = E_{\text{Fe}^{3+}/\text{Fe}^{2+}} - E_\text{SHE} = 0.750 \text{ V} -0.197 \text{ V} = 553 \text{ V} \nonumber\]
Figure \(\PageIndex{7}\) provides a pictorial representation of the relationship between these different potentials.
The potential of a \(\text{UO}_2^+\)/U4+ half-cell is –0.0190 V relative to a saturated calomel electrode. What is its potential when using a saturated silver/silver chloride electrode or a standard hydrogen electrode?
- Answer
-
When using a saturated calomel electrode, the potential of the electro- chemical cell is
\[E_\text{cell} = E_{\text{UO}_2^+/\text{U}^{4+}} - E_\text{SCE} \nonumber\]
Substituting in known values
\[-0.0190 \text{ V} = E_{\text{UO}_2^+/\text{U}^{4+}} - 0.2444 \text{ V} \nonumber\]
and solving for \(E_{\text{UO}_2^+/\text{U}^{4+}}\) gives its value as +0.2254 V. The potential relative to the Ag/AgCl electrode is
\[E_\text{cell} = E_{\text{UO}_2^+/\text{U}^{4+}} - E_\text{Ag/AgCl} = 0.2254 \text{ V} - 0.197 \text{ V} = 0.028 \text{ V} \nonumber\]
and the potential relative to the standard hydrogen electrode is
\[E_\text{cell} = E_{\text{UO}_2^+/\text{U}^{4+}} - E_\text{SHE} = 0.2254 \text{ V} - 0.000 \text{ V} = 0.2254 \text{ V} \nonumber\]
Metallic Indicator Electrodes
In potentiometry, the potential of the indicator electrode is proportional to the analyte’s activity. Two classes of indicator electrodes are used to make potentiometric measurements: metallic electrodes, which are the subject of this section, and ion-selective electrodes, which are covered in the next section.
Electrodes of the First Kind
If we place a copper electrode in a solution that contains Cu2+, the electrode’s potential due to the reaction
\[\mathrm{Cu}^{2+}(a q)+2 e^{-} \rightleftharpoons \mathrm{Cu}(s) \nonumber\]
is determined by the activity of Cu2+.
\[E=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\mathrm{o}}-\frac{0.05916}{2} \log \frac{1}{a_{\mathrm{Cu}^{2+}}}=+0.3419 \mathrm{V}-\frac{0.05916}{2} \log \frac{1}{a_{\mathrm{Cu}^{2+}}} \nonumber\]
If copper is the indicator electrode in a potentiometric electrochemical cell that also includes a saturated calomel reference electrode
\[\mathrm{SCE} \| \mathrm{Cu}^{2+}\left(a q, a_{\mathrm{Cu^{2+}}}=x\right) | \text{Cu}(s) \nonumber\]
then we can use the cell potential to determine an unknown activity of Cu2+ in the indicator electrode’s half-cell
\[E_{\text{cell}}= E_{\text { ind }}-E_{\text {SCE }}+E_{j}= +0.3419 \mathrm{V}-\frac{0.05916}{2} \log \frac{1}{a_{\mathrm{Cu}^{2+}}}-0.2224 \mathrm{V}+E_{j} \nonumber\]
An indicator electrode in which the metal is in contact with a solution containing its ion is called an electrode of the first kind. In general, if a metal, M, is in a solution of Mn+, the cell potential is
\[E_{\mathrm{call}}=K-\frac{0.05916}{n} \log \frac{1}{a_{M^{n+}}}=K+\frac{0.05916}{n} \log a_{M^{n+}} \nonumber\]
where K is a constant that includes the standard-state potential for the Mn+/M redox couple, the potential of the reference electrode, and the junction potential.
Note that including Ej in the constant K means we do not need to know the junction potential’s actual value; however, the junction potential must remain constant if K is to maintain a constant value.
For a variety of reasons—including the slow kinetics of electron transfer at the metal–solution interface, the formation of metal oxides on the electrode’s surface, and interfering reactions—electrodes of the first kind are limited to the following metals: Ag, Bi, Cd, Cu, Hg, Pb, Sn, Tl, and Zn.
Many of these electrodes, such as Zn, cannot be used in acidic solutions because they are easily oxidized by H+.
\[\mathrm{Zn}(s)+2 \mathrm{H}^{+}(a q)\rightleftharpoons \text{ H}_{2}(g)+\mathrm{Zn}^{2+}(a q) \nonumber\]
Electrodes of the Second Kind
The potential of an electrode of the first kind responds to the activity of Mn+. We also can use this electrode to determine the activity of another species if it is in equilibrium with Mn+. For example, the potential of a Ag electrode in a solution of Ag+ is
\[E=0.7996 \mathrm{V}+0.05916 \log a_{\mathrm{Ag}^{+}} \label{11.3}\]
If we saturate the indicator electrode’s half-cell with AgI, the solubility reaction
\[\operatorname{Agl}(s)\rightleftharpoons\operatorname{Ag}^{+}(a q)+\mathrm{I}^{-}(a q) \nonumber\]
determines the concentration of Ag+; thus
\[a_{\mathrm{Ag}^{+}}=\frac{K_{\mathrm{sp}, \mathrm{Agl}}}{a_{\text{I}^-}} \label{11.4}\]
where Ksp,AgI is the solubility product for AgI. Substituting equation \ref{11.4} into equation \ref{11.3}
\[E=0.7996 \text{ V}+0.05916 \log \frac{K_{\text{sp, Agl}}}{a_{\text{I}^-}} \nonumber\]
shows that the potential of the silver electrode is a function of the activity of I–. If we incorporate this electrode into a potentiometric electrochemical cell with a saturated calomel electrode
\[\mathrm{SCE} \| \mathrm{AgI}(s), \text{ I}^-\left(a q, a_{\text{I}^-}=x\right) | \mathrm{Ag}(\mathrm{s}) \nonumber\]
then the cell potential is
\[E_{\mathrm{cell}}=K-0.05916 \log a_{\text{I}^-} \nonumber\]
where K is a constant that includes the standard-state potential for the Ag+/Ag redox couple, the solubility product for AgI, the reference electrode’s potential, and the junction potential.
If an electrode of the first kind responds to the activity of an ion in equilibrium with Mn+, we call it an electrode of the second kind. Two common electrodes of the second kind are the calomel and the silver/silver chloride reference electrodes.
In an electrode of the second kind we link together a redox reaction and another reaction, such as a solubility reaction. You might wonder if we can link together more than two reactions. The short answer is yes. An electrode of the third kind, for example, links together a redox reaction and two other reactions. Such electrodes are less common and we will not consider them in this text.
Redox Electrodes
An electrode of the first kind or second kind develops a potential as the result of a redox reaction that involves the metallic electrode. An electrode also can serve as a source of electrons or as a sink for electrons in an unrelated redox reaction, in which case we call it a redox electrode. The Pt cathode in Figure \(\PageIndex{2}\) and Example \(\PageIndex{1}\) is a redox electrode because its potential is determined by the activity of Fe2+ and Fe3+ in the indicator half-cell. Note that a redox electrode’s potential often responds to the activity of more than one ion, which limits its usefulness for direct potentiometry.
Membrane Electrodes
If metals were the only useful materials for constructing indicator electrodes, then there would be few useful applications of potentiometry. In 1906, Cremer discovered that the potential difference across a thin glass membrane is a function of pH when opposite sides of the membrane are in contact with solutions that have different concentrations of H3O+. The existence of this membrane potential led to the development of a whole new class of indicator electrodes, which we call ion-selective electrodes (ISEs). In addition to the glass pH electrode, ion-selective electrodes are available for a wide range of ions. It also is possible to construct a membrane electrode for a neutral analyte by using a chemical reaction to generate an ion that is monitored with an ion-selective electrode. The development of new membrane electrodes continues to be an active area of research.
Membrane Potentials
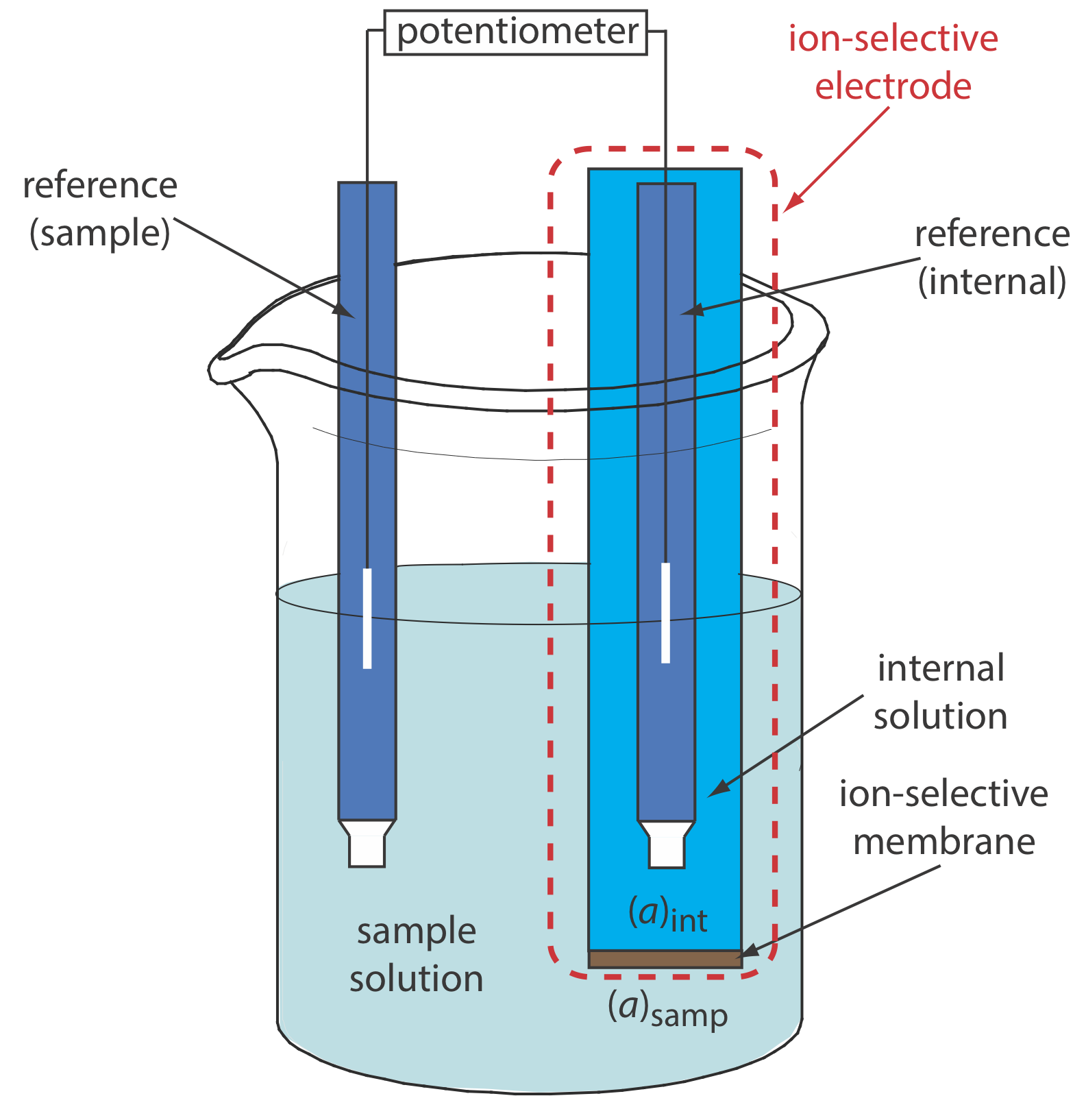
Figure \(\PageIndex{8}\) shows a typical potentiometric electrochemical cell equipped with an ion-selective electrode. The short hand notation for this cell is
\[\text { ref (sample) }\left\|[\mathrm{A}]_{\text { samp }}\left(a q, a_{\mathrm{A}}=x\right) |[\mathrm{A}]_{\text { int }}\left(a q, a_{\mathrm{A}}=y\right)\right\| \text { ref (internal) } \nonumber\]
where the ion-selective membrane is represented by the vertical slash that separates the two solutions that contain analyte: the sample solution and the ion-selective electrode’s internal solution. The potential of this electrochemical cell includes the potential of each reference electrode, a junction potential, and the membrane’s potential
\[E_\text{cell} = E_\text{ref(int)} - E_\text{ref(samp)} + E_\text{mem} + E_j \label{11.5}\]
where Emem is the potential across the membrane and The notations ref(sample) and ref(internal) represent a reference electrode immersed in the sample and a reference electrode immersed in the ISE’s internal solution. Because the junction potential and the potential of the two reference electrodes are constant, any change in Ecell reflects a change in the membrane’s potential.
The analyte’s interaction with the membrane generates a membrane potential if there is a difference in its activity on the membrane’s two sides. Current is carried through the membrane by the movement of either the analyte or an ion already present in the membrane’s matrix. The membrane potential is given by the following Nernst-like equation
\[E_{\mathrm{mem}}=E_{\mathrm{asym}}-\frac{R T}{z F} \ln \frac{\left(a_{A}\right)_{\mathrm{int}}}{\left(a_{A}\right)_{\mathrm{samp}}} \label{11.6}\]
where (aA)samp is the analyte’s activity in the sample, (aA)int is the analyte’s activity in the ion-selective electrode’s internal solution, and z is the analyte’s charge. Ideally, Emem is zero when (aA)int = (aA)samp. The term Easym, which is an asymmetry potential, accounts for the fact that Emem usually is not zero under these conditions.
For now we simply note that a difference in the analyte’s activity results in a membrane potential. As we consider different types of ion-selective electrodes, we will explore more specifically the source of the membrane potential.
Substituting equation \ref{11.6} into equation \ref{11.5}, assuming a temperature of 25oC, and rearranging gives
\[E_{\mathrm{cell}}=K+\frac{0.05916}{z} \log \left(a_{A}\right)_{\mathrm{samp}} \label{11.7}\]
where K is a constant that includes the potentials of the two reference electrodes, the junction potentials, the asymmetry potential, and the analyte's activity in the internal solution. Equation \ref{11.7} is a general equation and applies to all types of ion-selective electrodes.
Selectivity of Membranes
A membrane potential results from a chemical interaction between the analyte and active sites on the membrane’s surface. Because the signal depends on a chemical process, most membranes are not selective toward a single analyte. Instead, the membrane potential is proportional to the concentration of each ion that interacts with the membrane’s active sites. We can rewrite equation \ref{11.7} to include the contribution to the potential of an interferent, I
\[E_\text{cell} = K + \frac {0.05916} {z_A} \log \left\{ a_A + K_{A,I}(a_I)^{z_A/z_I} \right\} \nonumber\]
where zA and zI are the charges of the analyte and the interferent, and KA,I is a selectivity coefficient that accounts for the relative response of the interferent. The selectivity coefficient is defined as
\[K_{A,I} = \frac {(a_A)_e} {(a_I)_e^{z_A/z_I}} \label{11.8}\]
where (aA)e and (aI)e are the activities of analyte and the interferent that yield identical cell potentials. When the selectivity coefficient is 1.00, the membrane responds equally to the analyte and the interferent. A membrane shows good selectivity for the analyte when KA,I is significantly less than 1.00.
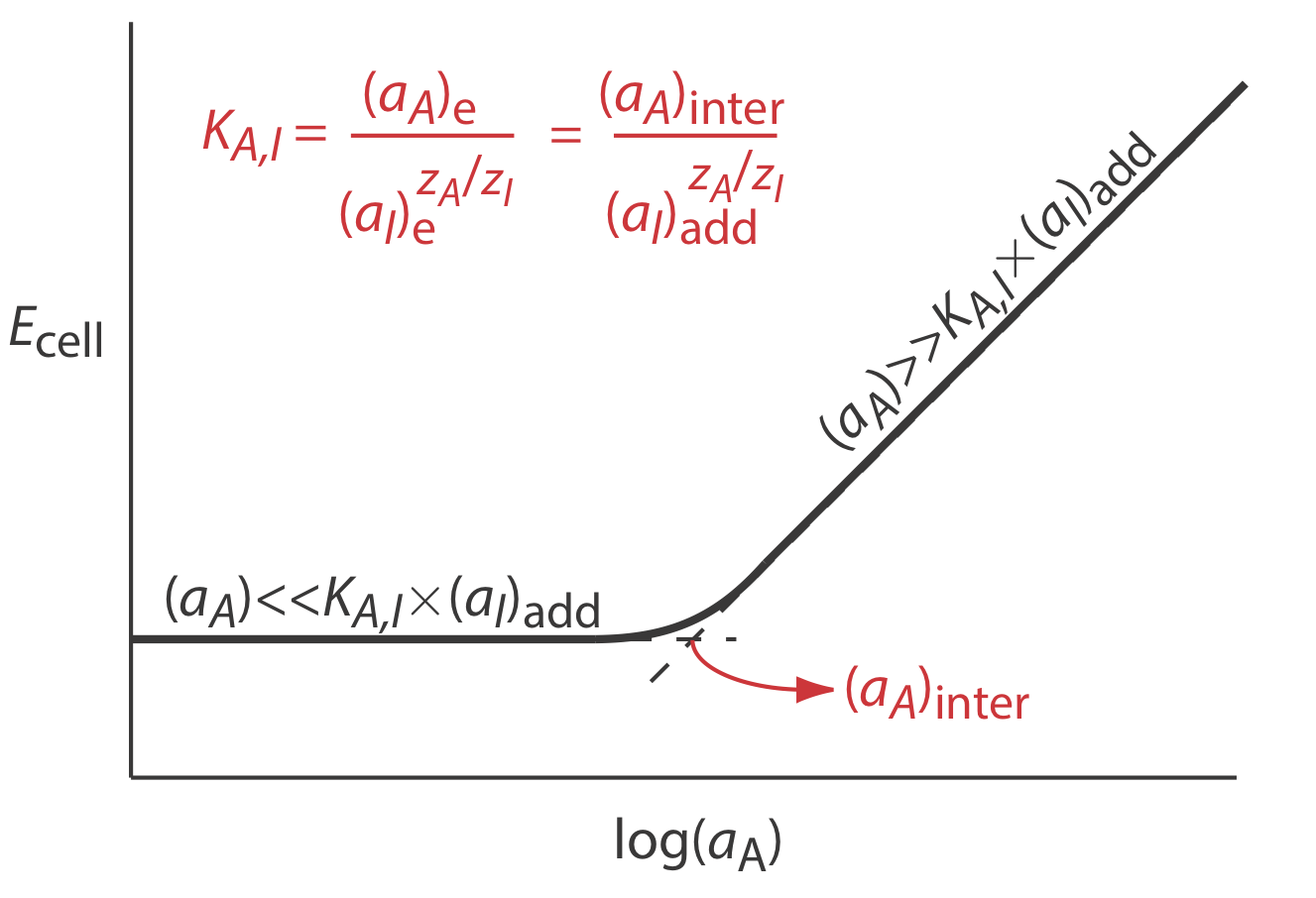
Selectivity coefficients for most commercially available ion-selective electrodes are provided by the manufacturer. If the selectivity coefficient is not known, it is easy to determine its value experimentally by preparing a series of solutions, each of which contains the same activity of interferent, (aI)add, but a different activity of analyte. As shown in Figure \(\PageIndex{9}\), a plot of cell potential versus the log of the analyte’s activity has two distinct linear regions. When the analyte’s activity is significantly larger than KA,I \(\times\) (aI)add, the potential is a linear function of log(aA), as given by equation \ref{11.7}. If KA,I \(\times\) (aI)add is significantly larger than the analyte’s activity, however, the cell’s potential remains constant. The activity of analyte and interferent at the intersection of these two linear regions is used to calculate KA,I.
Sokalski and co-workers described a method for preparing ion-selective electrodes with significantly improved selectivities [Sokalski, T.; Ceresa, A.; Zwicki, T.; Pretsch, E. J. Am. Chem. Soc. 1997, 119, 11347–11348]. For example, a conventional Pb2+ ISE has a \(\log K_{\text{Pb}^{2+}/\text{Mg}^{2+}}\) of –3.6. If the potential for a solution in which the activity of Pb2+ is \(4.1 \times 10^{-12}\) is identical to that for a solution in which the activity of Mg2+ is 0.01025, what is the value of \(\log K_{\text{Pb}^{2+}/\text{Mg}^{2+}}\) for their ISE?
Solution
Making appropriate substitutions into equation \ref{11.8}, we find that
\[K_{\text{Pb}^{2+}/\text{Mg}^{2+}} = \frac {(a_{\text{Pb}^{2+}})_e} {(a_{\text{Mg}^{2+}})_e^{z_{\text{Pb}^{2+}}/z_{\text{Mg}^{2+}}}} = \frac {4.1 \times 10^{-12}} {(0.01025)^{+2/+2}} = 4.0 \times 10^{-10} \nonumber\]
The value of \(\log K_{\text{Pb}^{2+}/\text{Mg}^{2+}}\), therefore, is –9.40.
A ion-selective electrode for \(\text{NO}_2^-\) has logKA,I values of –3.1 for F–, –4.1 for \(\text{SO}_4^{2-}\), –1.2 for I–, and –3.3 for \(\text{NO}_3^-\). Which ion is the most serious interferent and for what activity of this interferent is the potential equivalent to a solution in which the activity of \(\text{NO}_2^-\) is \(2.75 \times 10^{-4}\)?
- Answer
-
The larger the value of KA,I the more serious the interference. Larger values for KA,I correspond to more positive (less negative) values for logKA,I; thus, I–, with a KA,I of \(6.3 \times 10^{-2}\), is the most serious of these interferents. To find the activity of I– that gives a potential equivalent to a \(\text{NO}_2^-\) activity of \(2.75 \times 10^{-4}\), we note that
\[a_{\text{NO}_2^-}=K_{A, I} \times a_{\text{I}^-} \nonumber\]
Making appropriate substitutions
\[2.75 \times 10^{-4}=\left(6.3 \times 10^{-2}\right) \times a_{\mathrm{I}^-} \nonumber\]
and solving for \(a_{\text{I}^-}\) gives its activity as \(4.4 \times 10^{-3}\).
Glass Ion-Selective Electrodes
The first commercial glass electrodes were manufactured using Corning 015, a glass with a composition that is approximately 22% Na2O, 6% CaO, and 72% SiO2. When immersed in an aqueous solution for several hours, the outer approximately 10 nm of the membrane’s surface becomes hydrated, resulting in the formation of negatively charged sites, —SiO–. Sodium ions, Na+, serve as counter ions. Because H+ binds more strongly to —SiO– than does Na+, they displace the sodium ions
\[\mathrm{H}^{+}+-\mathrm{SiO}^{-} \mathrm{Na}^{+}\rightleftharpoons-\mathrm{SiO}^{-} \mathrm{H}^{+}+\mathrm{Na}^{+} \nonumber\]
explaining the membrane’s selectivity for H+. The transport of charge across the membrane is carried by the Na+ ions. The potential of a glass electrode using Corning 015 obeys the equation
\[E_{\mathrm{cell}}=K+0.05916 \log a_{\mathrm{H}^{+}} \label{11.9}\]
glass membrane is more responsive to other cations, such as Na+ and K+.
For a Corning 015 glass membrane, the selectivity coefficient KH+/Na+ is \(\approx 10^{-11}\). What is the expected error if we measure the pH of a solution in which the activity of H+ is \(2 \times 10^{-13}\) and the activity of Na+ is 0.05?
Solution
A solution in which the actual activity of H+, (aH+)act, is \(2 \times 10^{-13}\) has a pH of 12.7. Because the electrode responds to both H+ and Na+, the apparent activity of H+, (aH+)app, is
\[(a_{\text{H}^+})_\text{app} = (a_{\text{H}^+})_\text{act} + (K_{\text{H}^+ / \text{Na}^+} \times a_{\text{Na}^+}) = 2 \times 10^{-13} + (10^{-11} \times 0.05) = 7 \times 10^{-13} \nonumber\]
The apparent activity of H+ is equivalent to a pH of 12.2, an error of –0.5 pH units.
Replacing Na2O and CaO with Li2O and BaO extends the useful pH range of glass membrane electrodes to pH levels greater than 12.
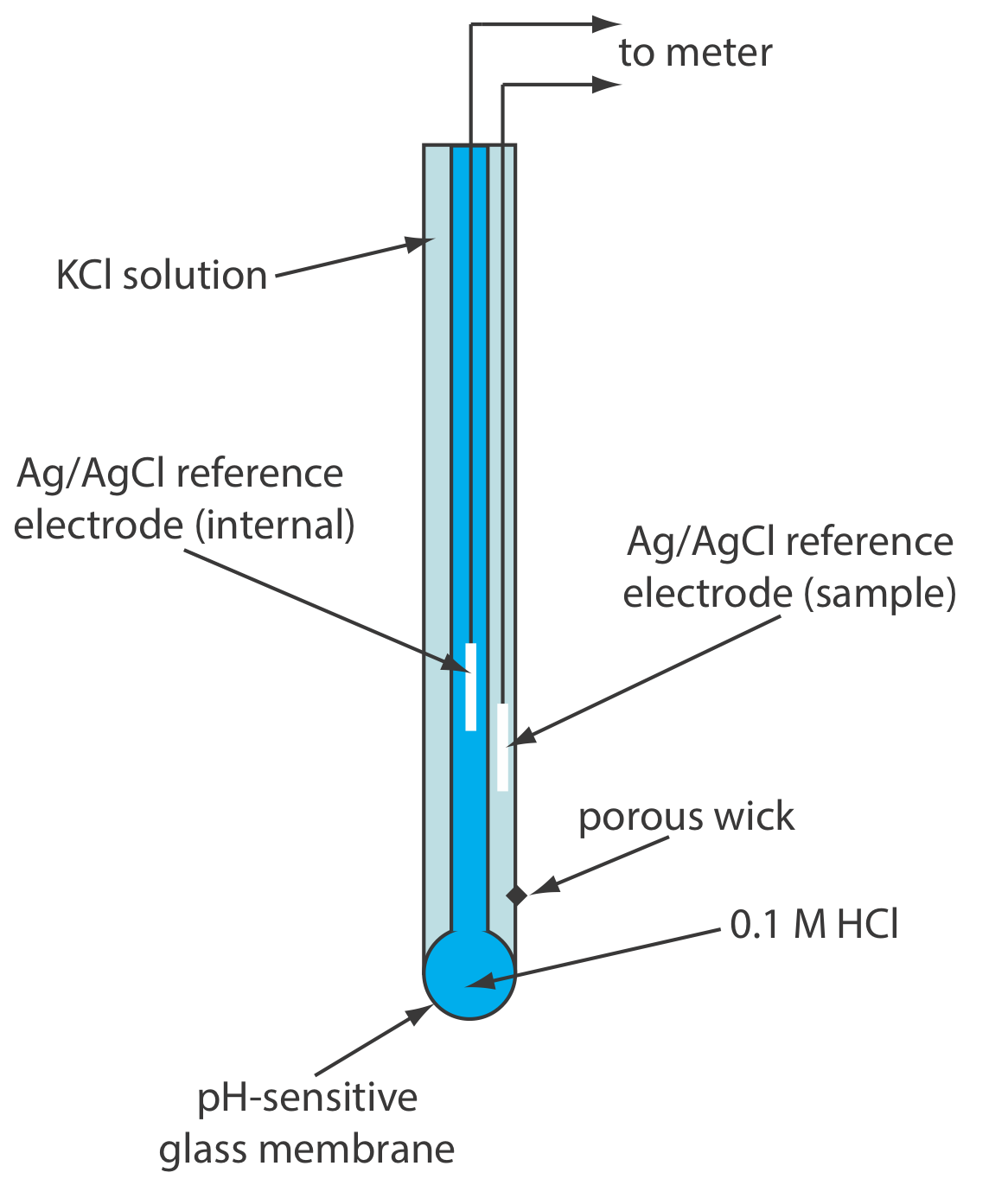
Glass membrane pH electrodes often are available in a combination form that includes both the indicator electrode and the reference electrode. The use of a single electrode greatly simplifies the measurement of pH. An example of a typical combination electrode is shown in Figure \(\PageIndex{10}\).
The observation that the Corning 015 glass membrane responds to ions other than H+ (see Example \(\PageIndex{6}\)) led to the development of glass membranes with a greater selectivity for other cations. For example, a glass membrane with a composition of 11% Na2O, 18% Al2O3, and 71% SiO2 is used as an ion-selective electrode for Na+. Other glass ion-selective electrodes have been developed for the analysis of Li+, K+, Rb+, Cs+, \(\text{NH}_4^+\) , Ag+, and Tl+. Table \(\PageIndex{1}\) provides several examples.
Because an ion-selective electrode’s glass membrane is very thin—it is only about 50 μm thick—they must be handled with care to avoid cracks or breakage. Glass electrodes usually are stored in a storage buffer recommended by the manufacturer, which ensures that the membrane’s outer surface remains hydrated. If a glass electrode dries out, it is reconditioned by soaking for several hours in a solution that contains the analyte. The composition of a glass membrane will change over time, which affects the electrode’s performance. The average lifetime for a typical glass electrode is several years.
Solid-State Ion-Selective Electrodes
A solid-state ion-selective electrode has a membrane that consists of either a polycrystalline inorganic salt or a single crystal of an inorganic salt. We can fashion a polycrystalline solid-state ion-selective electrode by sealing a 1–2 mm thick pellet of AgS—or a mixture of AgS and a second silver salt or another metal sulfide—into the end of a nonconducting plastic cylinder, filling the cylinder with an internal solution that contains the analyte, and placing a reference electrode into the internal solution. Figure \(\PageIndex{11}\) shows a typical design.
The NaCl in a salt shaker is an example of polycrystalline material because it consists of many small crystals of sodium chloride. The NaCl salt plates used in IR spectroscopy (see Chapter 10), on the other hand, are an example of a single crystal of sodium chloride.

The membrane potential for a Ag2S pellet develops as the result of a difference in the extent of the solubility reaction
\[\mathrm{Ag}_{2} \mathrm{S}(s)\rightleftharpoons2 \mathrm{Ag}^{+}(a q)+\mathrm{S}^{2-}(a q) \nonumber\]
on the membrane’s two sides, with charge carried across the membrane by Ag+ ions. When we use the electrode to monitor the activity of Ag+, the cell potential is
\[E_{\text {cell }}=K+0.05916 \log a_{\mathrm{Ag}^{+}} \nonumber\]
The membrane also responds to the activity of \(\text{S}^{2-}\), with a cell potential of
\[E_{\mathrm{cell}}=K-\frac{0.05916}{2} \log a_{\text{S}^{2-}} \nonumber\]
If we combine an insoluble silver salt, such as AgCl, with the Ag2S, then the membrane potential also responds to the concentration of Cl–, with a cell potential of
\[E_{\text {cell }}=K-0.05916 \log a_{\mathrm{Cl}^{-}} \nonumber\]
By mixing Ag2S with CdS, CuS, or PbS, we can make an ion-selective electrode that responds to the activity of Cd2+, Cu2+, or Pb2+. In this case the cell potential is
\[E_{\mathrm{cell}}=K+\frac{0.05916}{2} \ln a_{M^{2+}} \nonumber\]
where aM2+ is the activity of the metal ion.
Table \(\PageIndex{2}\) provides examples of polycrystalline, Ag2S-based solid-state ion-selective electrodes. The selectivity of these ion-selective electrodes depends on the relative solubility of the compounds. A Cl– ISE using a Ag2S/AgCl membrane is more selective for Br– (KCl–/Br– = 102) and for I– (KCl–/I– = 106) because AgBr and AgI are less soluble than AgCl. If the activity of Br– is sufficiently high, AgCl at the membrane/solution interface is replaced by AgBr and the electrode’s response to Cl– decreases substantially. Most of the polycrystalline ion-selective electrodes listed in Table \(\PageIndex{2}\) operate over an extended range of pH levels. The equilibrium between S2– and HS– limits the analysis for S2– to a pH range of 13–14.
The membrane of a F– ion-selective electrode is fashioned from a single crystal of LaF3, which usually is doped with a small amount of EuF2 to enhance the membrane’s conductivity. Because EuF2 provides only two F– ions—compared to the three F– ions in LaF3—each EuF2 produces a vacancy in the crystal’s lattice. Fluoride ions pass through the membrane by moving into adjacent vacancies. As shown in Figure \(\PageIndex{11}\), the LaF3 membrane is sealed into the end of a non-conducting plastic cylinder, which contains a standard solution of F–, typically 0.1 M NaF, and a Ag/AgCl reference electrode.
The membrane potential for a F– ISE results from a difference in the solubility of LaF3 on opposite sides of the membrane, with the potential given by
\[E_{\mathrm{cell}}=K-0.05916 \log a_{\mathrm{F}^-} \nonumber\]
One advantage of the F– ion-selective electrode is its freedom from interference. The only significant exception is OH– (KF–/OH– = 0.1), which imposes a maximum pH limit for a successful analysis. Below a pH of 4 the predominate form of fluoride in solution is HF, which does not contribute to the membrane potential. For this reason, an analysis for fluoride is carried out at a pH greater than 4.
What is the maximum pH that we can tolerate if we need to analyze a solution in which the activity of F– is \(1 \times 10^{-5}\) with an error of less than 1%?
Solution
In the presence of OH– the cell potential is
\[E_{\mathrm{cell}}=K-0.05916\left\{a_{\mathrm{F}^-}+K_{\mathrm{F}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^-}\right\} \nonumber\]
To achieve an error of less than 1%, the term \(K_{\mathrm{F}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^-}\) must be less than 1% of aF–; thus
\[K_{\mathrm{F}^- / \mathrm{OH}^-} \times a_{\mathrm{OH}^{-}} \leq 0.01 \times a_{\mathrm{F}^-} \nonumber\]
\[0.10 \times a_{\mathrm{OH}^{-}} \leq 0.01 \times\left(1.0 \times 10^{-5}\right) \nonumber\]
Solving for aOH– gives the maximum allowable activity for OH– as \(1 \times 10^{-6}\), which corresponds to a pH of less than 8.
Suppose you wish to use the nitrite-selective electrode in Exercise \(\PageIndex{5}\) to measure the activity of \(\text{NO}_2^-\). If the activity of \(\text{NO}_2^-\) is \(2.2 \times 10^{-4}\), what is the maximum pH you can tolerate if the error due to OH– must be less than 10%? The selectivity coefficient for OH–, \(K_{\text{NO}_2^-/\text{OH}^-}\), is 630. Do you expect the electrode to have a lower pH limit? Clearly explain your answer.
- Answer
-
In the presence of OH– the cell potential is
\[E_{\mathrm{cell}}=K-0.05916 \log \left\{a_{\mathrm{NO}_{2}^-}+K_{\mathrm{NO}_{2}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^{-}}\right\} \nonumber\]
To achieve an error of less than 10%, the term \(K_{\mathrm{NO}_{2}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^{-}}\) must be less than 1% of \(a_{\text{NO}_2^-}\); thus
\[K_{\mathrm{NO}_{2}^- / \mathrm{OH}^{-}} \times a_{\mathrm{OH}^-} \leq 0.10 \times a_{\mathrm{NO}_{2}^-} \nonumber\]
\[630 \times a_{\mathrm{OH}^{-}} \leq 0.10 \times\left(2.2 \times 10^{-4}\right) \nonumber\]
Solving for aOH– gives its maximum allowable activity as \(3.5 \times 10^{-8}\), which corresponds to a pH of less than 6.54.
The electrode does have a lower pH limit. Nitrite is the conjugate weak base of HNO2, a species to which the ISE does not respond. As shown by the ladder diagram below, at a pH of 4.15 approximately 10% of nitrite is present as HNO2. A minimum pH of 4.5 is the usual recommendation when using a nitrite ISE. This corresponds to a \(\text{NO}_2^- / \text{HNO}_2\) ratio of
\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\mathrm{NO}_{2}^{-}\right]}{\left[\mathrm{HNO}_{2}\right]} \nonumber\]
\[4.5=3.15+\log \frac{\left[\mathrm{NO}_{2}^{-}\right]}{\left[\mathrm{HNO}_{2}\right]} \nonumber\]
\[\frac{\left[\mathrm{NO}_{2}^{-}\right]}{\left[\mathrm{HNO}_{2}\right]} \approx 22 \nonumber\]
Thus, at a pH of 4.5 approximately 96% of nitrite is present as \(\text{NO}_2^-\).
Unlike a glass membrane ion-selective electrode, a solid-state ISE does not need to be conditioned before it is used, and it may be stored dry. The surface of the electrode is subject to poisoning, as described above for a Cl– ISE in contact with an excessive concentration of Br–. If an electrode is poisoned, it can be returned to its original condition by sanding and polishing the crystalline membrane.
Poisoning simply means that the surface has been chemically modified, such as AgBr forming on the surface of a AgCl membrane.
Liquid-Based Ion-Selective Electrodes
Another class of ion-selective electrodes uses a hydrophobic membrane that contains a liquid organic complexing agent that reacts selectively with the analyte. Three types of organic complexing agents have been used: cation exchangers, anion exchangers, and neutral ionophores. A membrane potential exists if the analyte’s activity is different on the two sides of the membrane. Current is carried through the membrane by the analyte.
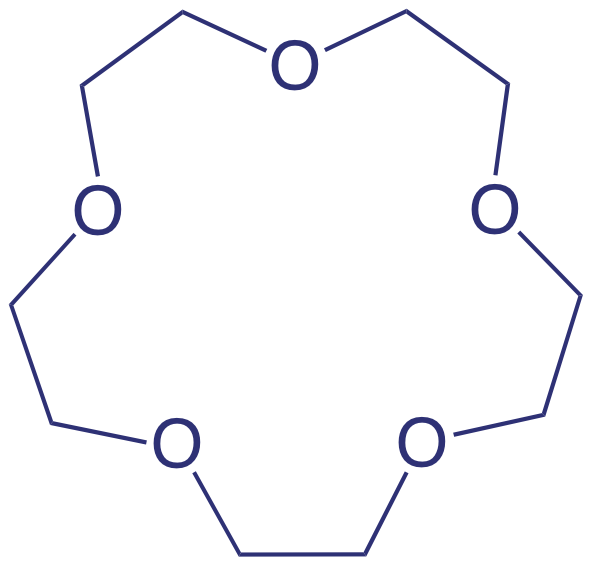
An ionophore is a ligand whose exterior is hydrophobic and whose interior is hydrophilic. The crown ether shown here is one example of a neutral ionophore.
One example of a liquid-based ion-selective electrode is that for Ca2+, which uses a porous plastic membrane saturated with the cation exchanger di-(n-decyl) phosphate. As shown in Figure \(\PageIndex{12}\), the membrane is placed at the end of a non-conducting cylindrical tube and is in contact with two reservoirs. The outer reservoir contains di-(n-decyl) phosphate in di-n-octylphenylphosphonate, which soaks into the porous membrane. The inner reservoir contains a standard aqueous solution of Ca2+ and a Ag/AgCl reference electrode. Calcium ion-selective electrodes also are available in which the di-(n-decyl) phosphate is immobilized in a polyvinyl chloride (PVC) membrane that eliminates the need for the outer reservoir.
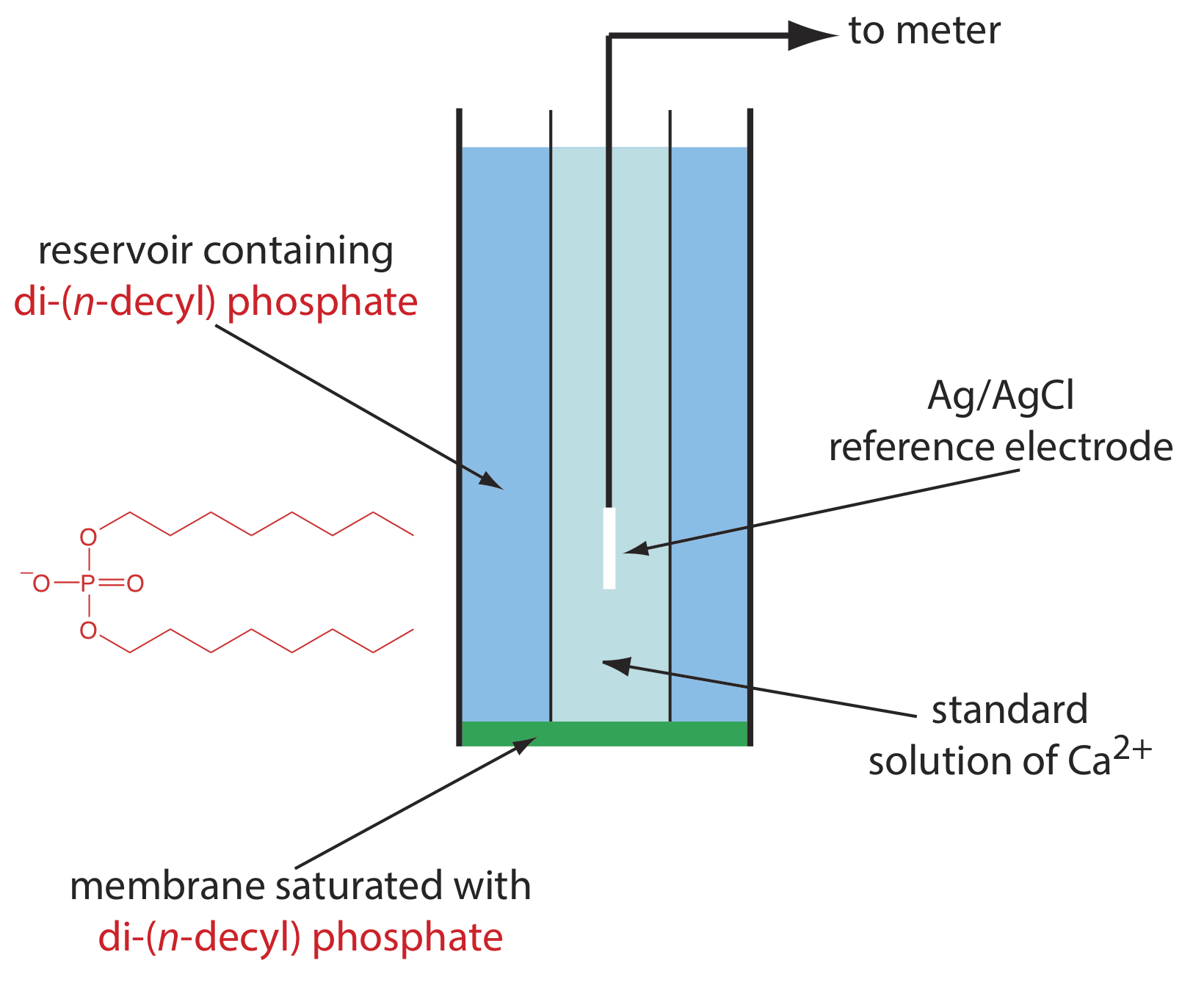
The membrane potential for the Ca2+ ISE develops as the result of a difference in the extent of the complexation reaction
\[\mathrm{Ca}^{2+}(a q)+2\left(\mathrm{C}_{10} \mathrm{H}_{21} \mathrm{O}\right)_{2} \mathrm{PO}_{2}^{-}(mem) \rightleftharpoons \mathrm{Ca}\left[\left(\mathrm{C}_{10} \mathrm{H}_{21} \mathrm{O}\right)_{2} \mathrm{PO}_{2}\right]_2 (mem) \nonumber\]
on the two sides of the membrane, where (mem) indicates a species that is present in the membrane. The cell potential for the Ca2+ ion-selective electrode is
\[E_{\mathrm{cell}}=K+\frac{0.05916}{2} \log a_{\mathrm{ca}^{2+}} \nonumber\]
The selectivity of this electrode for Ca2+ is very good, with only Zn2+ showing greater selectivity.
Table \(\PageIndex{3}\) lists the properties of several liquid-based ion-selective electrodes. An electrode using a liquid reservoir can be stored in a dilute solution of analyte and needs no additional conditioning before use. The lifetime of an electrode with a PVC membrane, however, is proportional to its exposure to aqueous solutions. For this reason these electrodes are best stored by covering the membrane with a cap along with a small amount of wetted gauze to maintain a humid environment. Before using the electrode it is conditioned in a solution of analyte for 30–60 minutes.
Gas-Sensing Electrodes
A number of membrane electrodes respond to the concentration of a dissolved gas. The basic design of a gas-sensing electrode, as shown in Figure \(\PageIndex{13}\), consists of a thin membrane that separates the sample from an inner solution that contains an ion-selective electrode. The membrane is permeable to the gaseous analyte, but impermeable to nonvolatile components in the sample’s matrix. The gaseous analyte passes through the membrane where it reacts with the inner solution, producing a species whose concentration is monitored by the ion-selective electrode. For example, in a CO2 electrode, CO2 diffuses across the membrane where it reacts in the inner solution to produce H3O+.
\[\mathrm{CO}_{2}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\text{ HCO}_{3}^{-}(a q)+\text{ H}_{3} \mathrm{O}^{+}(a q) \label{11.10}\]
The change in the activity of H3O+ in the inner solution is monitored with a pH electrode, for which the cell potential is given by equation \ref{11.9}. To find the relationship between the activity of H3O+ in the inner solution and the activity of CO2 in the inner solution we rearrange the equilibrium constant expression for reaction \ref{11.10}; thus
\[a_{\mathrm{H}_{3} \mathrm{O}^{+}}=K_{\mathrm{a}} \times \frac{a_{\mathrm{CO}_{2}}}{a_{\mathrm{HCO}_{3}^{-}}} \label{11.11}\]
where Ka is the equilibrium constant. If the activity of \(\text{HCO}_3^-\) in the internal solution is sufficiently large, then its activity is not affected by the small amount of CO2 that passes through the membrane. Substituting equation \ref{11.11} into equation \ref{11.9} gives
\[E_{\mathrm{cell}}=K^{\prime}+0.05916 \log a_{\mathrm{co}_{2}} \nonumber\]
where K′ is a constant that includes the constant for the pH electrode, the equilibrium constant for reaction \ref{11.10} and the activity of \(\text{HCO}_3^-\) in the inner solution.
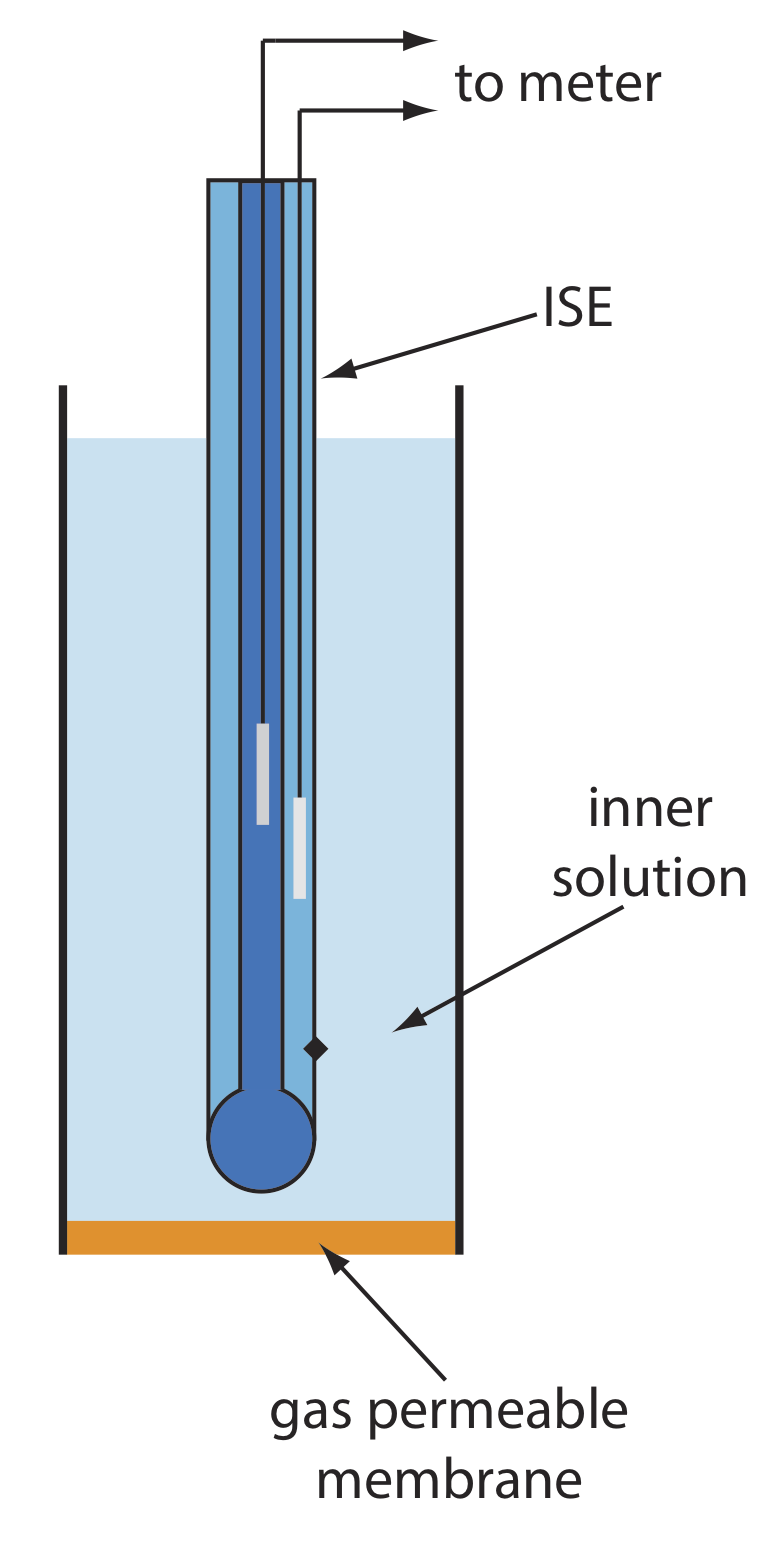
Table \(\PageIndex{4}\) lists the properties of several gas-sensing electrodes. The composition of the inner solution changes with use, and both the inner solution and the membrane must be replaced periodically. Gas-sensing electrodes are stored in a solution similar to the internal solution to minimize their exposure to atmospheric gases.
Potentiometric Biosensors
The approach for developing gas-sensing electrodes can be modified to create potentiometric electrodes that respond to a biochemically important species. The most common class of potentiometric biosensors are enzyme electrodes, in which we trap or immobilize an enzyme at the surface of a potentiometric electrode. The analyte’s reaction with the enzyme produces a product whose concentration is monitored by the potentiometric electrode. Potentiometric biosensors also have been designed around other biologically active species, including antibodies, bacterial particles, tissues, and hormone receptors.
One example of an enzyme electrode is the urea electrode, which is based on the catalytic hydrolysis of urea by urease
\[\mathrm{CO}\left(\mathrm{NH}_{2}\right)_{2}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons 2 \mathrm{NH}_{4}^{+}(a q)+\text{ CO}_{3}^{-}(a q) \nonumber\]
Figure \(\PageIndex{14}\) shows one version of the urea electrode, which modifies a gas-sensing NH3 electrode by adding a dialysis membrane that traps a pH 7.0 buffered solution of urease between the dialysis membrane and the gas permeable membrane [(a) Papastathopoulos, D. S.; Rechnitz, G. A. Anal. Chim. Acta 1975, 79, 17–26; (b) Riechel, T. L. J. Chem. Educ. 1984, 61, 640–642]. An NH3 electrode, as shown in Table \(\PageIndex{4}\), uses a gas-permeable membrane and a glass pH electrode. The NH3 diffuses across the membrane where it changes the pH of the internal solution.
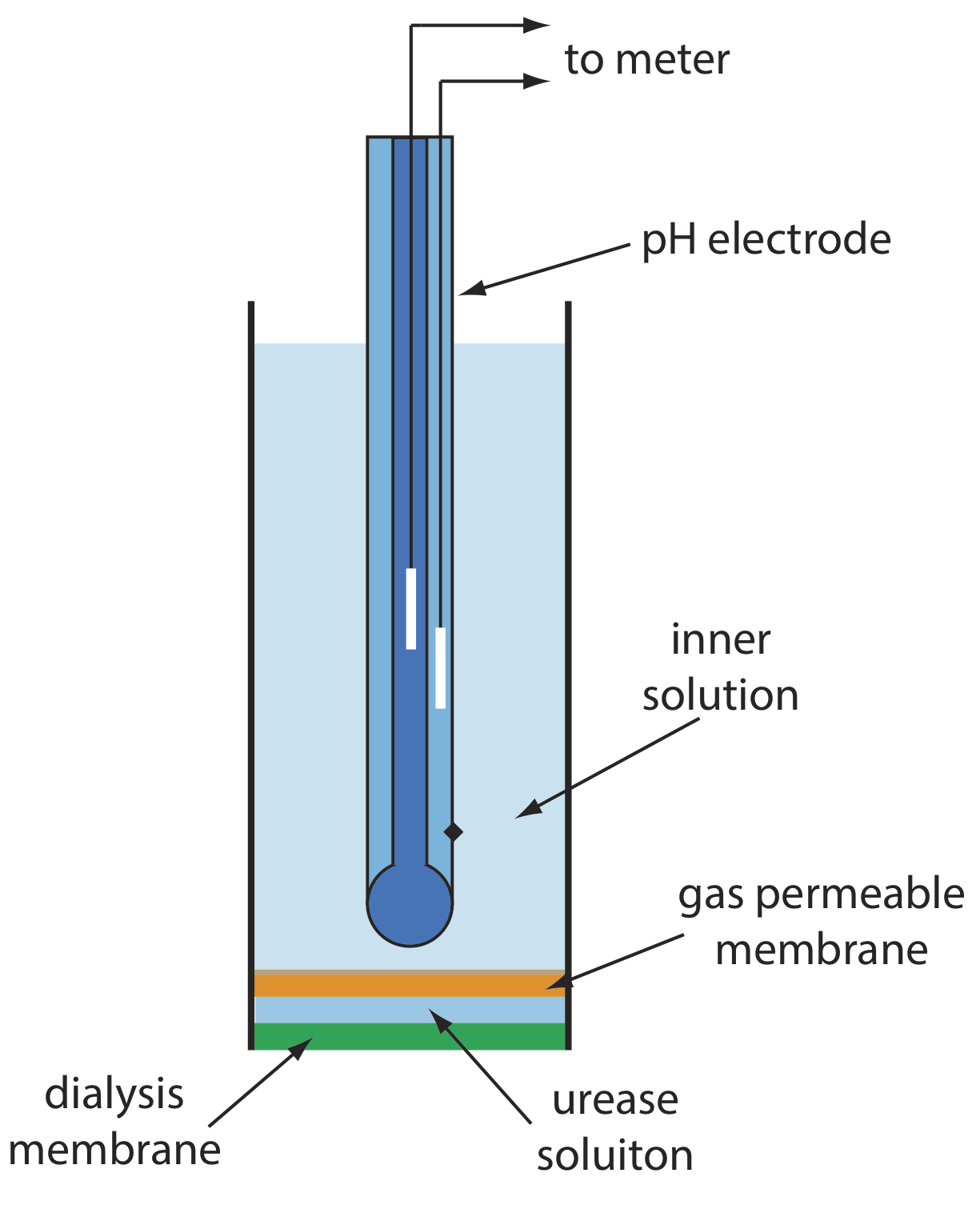
When immersed in the sample, urea diffuses through the dialysis membrane where it reacts with the enzyme urease to form the ammonium ion, \(\text{NH}_4^+\), which is in equilibrium with NH3.
\[\mathrm{NH}_{4}^{+}(a q)+\mathrm{H}_{2} \mathrm{O}(l ) \rightleftharpoons \text{ H}_{3} \mathrm{O}^{+}(a q)+\text{ NH}_{3}(a q) \nonumber\]
The NH3, in turn, diffuses through the gas permeable membrane where a pH electrode measures the resulting change in pH. The electrode’s response to the concentration of urea is
\[E_{\text {cell }}=K-0.05916 \log a_{\text {urea }} \label{11.12}\]
Another version of the urea electrode (Figure \(\PageIndex{15}\)) immobilizes the enzyme urease in a polymer membrane formed directly on the tip of a glass pH electrode [Tor, R.; Freeman, A. Anal. Chem. 1986, 58, 1042–1046]. In this case the response of the electrode is
\[\mathrm{pH}=K a_{\mathrm{urea}} \label{11.13}\]
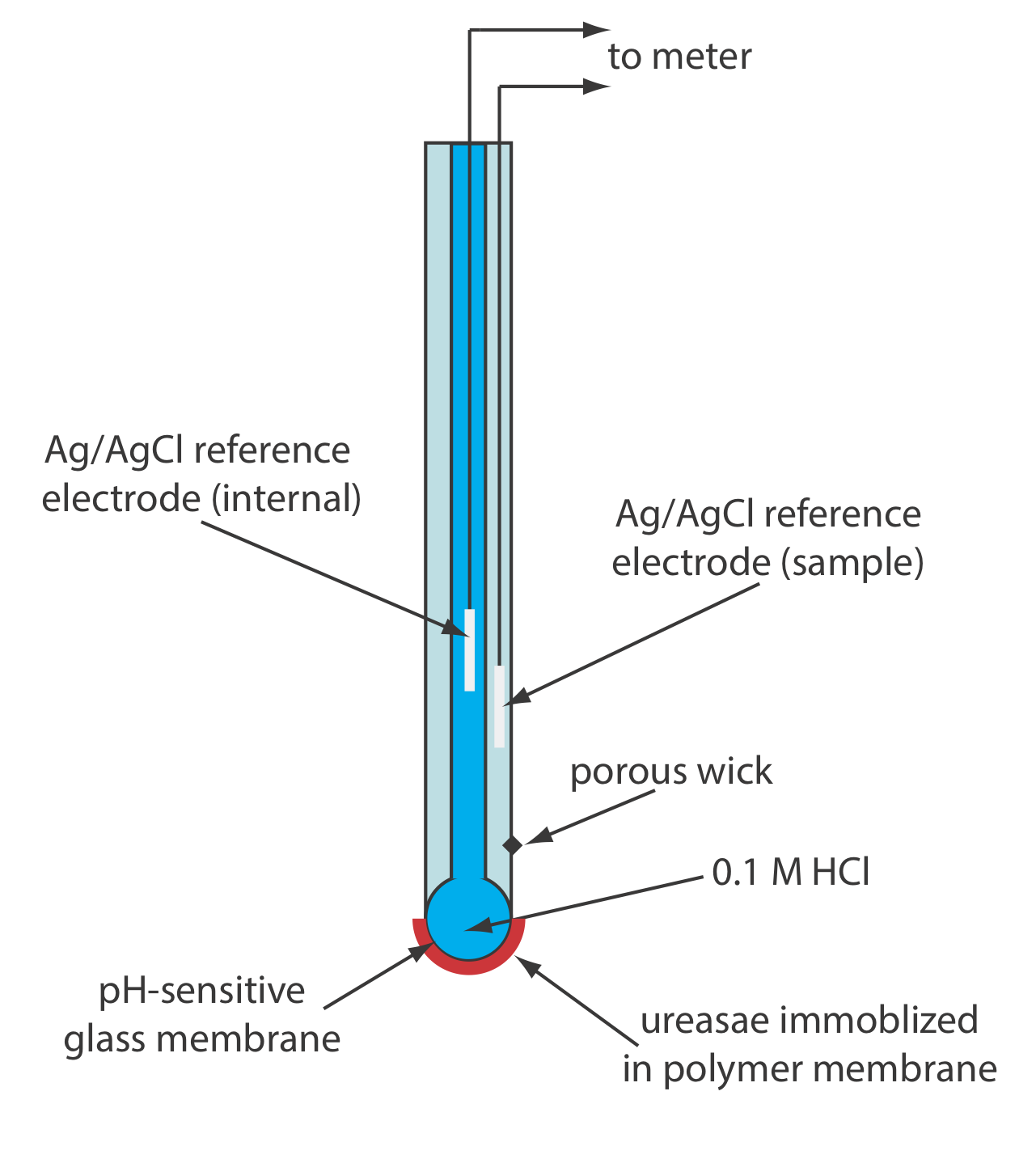
Few potentiometric biosensors are available commercially. As shown in Figure \(\PageIndex{14}\) and Figure \(\PageIndex{15}\), however, it is possible to convert an ion-selective electrode or a gas-sensing electrode into a biosensor. Several representative examples are described in Table \(\PageIndex{5}\), and additional examples can be found in this chapter’s additional resources.
Quantitative Applications
The potentiometric determination of an analyte’s concentration is one of the most common quantitative analytical techniques. Perhaps the most frequent analytical measurement is the determination of a solution’s pH, a measurement we will consider in more detail later in this section. Other areas where potentiometry is important are clinical chemistry, environmental chemistry, and potentiometric titrations. Before we consider representative applications, however, we need to examine more closely the relationship between cell potential and the analyte’s concentration and methods for standardizing potentiometric measurements.
Activity and Concentration
The Nernst equation relates the cell potential to the analyte’s activity. For example, the Nernst equation for a metallic electrode of the first kind is
\[E_{\mathrm{cll}}=K+\frac{0.05916}{n} \log a_{M^{n+}} \label{11.14}\]
where aMn+ is the metal ion’s activity. When we use a potentiometric electrode, however, our goal is to determine the analyte’s concentration. As we learned in Chapter 6, an ion’s activity is the product of its concentration, [Mn+], and a matrix-dependent activity coefficient, \(\gamma_{Mn^{n+}}\).
\[a_{M^{n+}}=\left[M^{n+}\right] \gamma_{M^{n+}} \label{11.15}\]
Substituting equation \ref{11.15} into equation \ref{11.14} and rearranging, gives
\[E_{\mathrm{cell}}=K+\frac{0.05916}{n} \log \gamma_{M^{n+}}+\frac{0.05916}{n} \log \left[M^{n+}\right] \label{11.16}\]
We can solve equation \ref{11.16} for the metal ion’s concentration if we know the value for its activity coefficient. Unfortunately, if we do not know the exact ionic composition of the sample’s matrix—which is the usual situation—then we cannot calculate the value of \(\gamma_{Mn^{n+}}\). There is a solution to this dilemma. If we design our system so that the standards and the samples have an identical matrix, then the value of \(\gamma_{Mn^{n+}}\) remains constant and equation \ref{11.16} simplifies to
\[E_{\mathrm{coll}}=K^{\prime}+\frac{0.05916}{n} \log \left[M^{n+}\right] \nonumber\]
where \(K^{\prime}\) includes the activity coefficient.
Quantitative Analysis Using External Standards
Before we can determine the concentration of analyte in a sample, we must standardize the electrode. If the electrode’s response obeys the Nernst equation, then we can determine the constant K using a single external standard. Because a small deviation from the ideal slope of ±RT/nF or ±RT/zF is not unexpected, we usually use two or more external standards.
To review the use of external standards, see Chapter 5.3.
In the absence of interferents, a calibration curve of Ecell versus logaA, where A is the analyte, is a straight-line. A plot of Ecell versus log[A], however, may show curvature at higher concentrations of analyte as a result of a matrix-dependent change in the analyte’s activity coefficient. To maintain a consistent matrix we add a high concentration of an inert electrolyte to all samples and standards. If the concentration of added electrolyte is sufficient, then the difference between the sample’s matrix and the matrix of the standards will not affect the ionic strength and the activity coefficient essentially remains constant. The inert electrolyte added to the sample and the standards is called a total ionic strength adjustment buffer (TISAB).
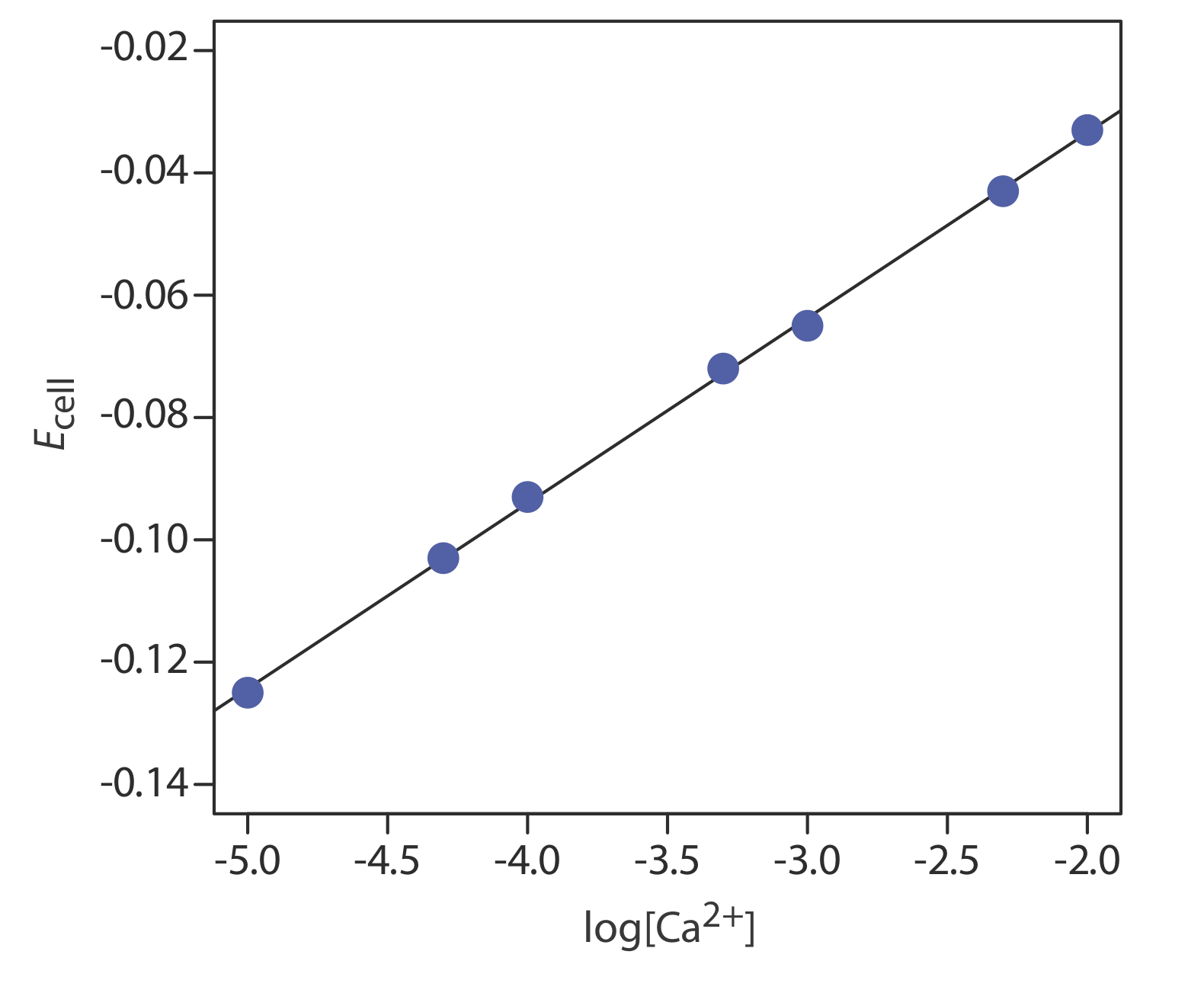
The concentration of Ca2+ in a water sample is determined using the method of external standards. The ionic strength of the samples and the standards is maintained at a nearly constant level by making each solution 0.5 M in KNO3. The measured cell potentials for the external standards are shown in the following table.
| [Ca2+] (M) | Ecell (V) |
|---|---|
|
\(1.00 \times 10^{-5}\) |
–0.125 |
| \(5.00 \times 10^{-5}\) | –0.103 |
| \(1.00 \times 10^{-4}\) | –0.093 |
| \(5.00 \times 10^{-4}\) | –0.072 |
| \(1.00 \times 10^{-3}\) | –0.063 |
| \(5.00 \times 10^{-3}\) | –0.043 |
| \(1.00 \times 10^{-2}\) | –0.033 |
What is the concentration of Ca2+ in a water sample if its cell potential is found to be –0.084 V?
Solution
Linear regression gives the calibration curve in Figure \(\PageIndex{16}\), with an equation of
\[E_{\mathrm{cell}}=0.027+0.0303 \log \left[\mathrm{Ca}^{2+}\right] \nonumber\]
Substituting the sample’s cell potential gives the concentration of Ca2+ as \(2.17 \times 10^{-4}\) M. Note that the slope of the calibration curve, which is 0.0303, is slightly larger than its ideal value of 0.05916/2 = 0.02958; this is not unusual and is one reason for using multiple standards.
One reason that it is not unusual to find that the experimental slope deviates from its ideal value of 0.05916/n is that this ideal value assumes that the temperature is 25°C.
Quantitative Analysis Using the Method of Standard Additions
Another approach to calibrating a potentiometric electrode is the method of standard additions. First, we transfer a sample with a volume of Vsamp and an analyte concentration of Csamp into a beaker and measure the potential, (Ecell)samp. Next, we make a standard addition by adding to the sample a small volume, Vstd, of a standard that contains a known concentration of analyte, Cstd, and measure the potential, (Ecell)std. If Vstd is significantly smaller than Vsamp, then we can safely ignore the change in the sample’s matrix and assume that the analyte’s activity coefficient is constant. Example \(\PageIndex{9}\) demonstrates how we can use a one-point standard addition to determine the concentration of analyte in a sample.
To review the method of standard additions, see Chapter 5.3.
The concentration of Ca2+ in a sample of sea water is determined using a Ca ion-selective electrode and a one-point standard addition. A 10.00-mL sample is transferred to a 100-mL volumetric flask and diluted to volume. A 50.00-mL aliquot of the sample is placed in a beaker with the Ca ISE and a reference electrode, and the potential is measured as –0.05290 V. After adding a 1.00-mL aliquot of a \(5.00 \times 10^{-2}\) M standard solution of Ca2+ the potential is –0.04417 V. What is the concentration of Ca2+ in the sample of sea water?
Solution
To begin, we write the Nernst equation before and after adding the standard addition. The cell potential for the sample is
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{samp}}=K+\frac{0.05916}{2} \log C_{\mathrm{samp}} \nonumber\]
and that following the standard addition is
\[\left(E_{\mathrm{cell}}\right)_{\mathrm{std}}=K+\frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} \nonumber\]
where Vtot is the total volume (Vsamp + Vstd) after the standard addition. Subtracting the first equation from the second equation gives
\[\Delta E = \left(E_{\mathrm{cell}}\right)_{\mathrm{std}} - \left(E_{\mathrm{cell}}\right)_{\mathrm{samp}} = \frac{0.05916}{2} \log \left\{ \frac {V_\text{samp}} {V_\text{tot}}C_\text{samp} + \frac {V_\text{std}} {V_\text{tot}}C_\text{std} \right\} - \frac{0.05916}{2}\log C_\text{samp} \nonumber\]
Rearranging this equation leaves us with
\[\frac{2 \Delta E_{cell}}{0.05916} = \log \left\{ \frac {V_\text{samp}} {V_\text{tot}} + \frac {V_\text{std}C_\text{std}} {V_\text{tot}C_\text{samp}} \right\} \nonumber\]
Substituting known values for \(\Delta E\), Vsamp, Vstd, Vtot and Cstd,
\[\begin{array}{l}{\frac{2 \times\{-0.04417-(-0.05290)\}}{0.05916}=} \\ {\log \left\{\frac{50.00 \text{ mL}}{51.00 \text{ mL}}+\frac{(1.00 \text{ mL})\left(5.00 \times 10^{-2} \mathrm{M}\right)}{(51.00 \text{ mL}) C_{\mathrm{samp}}}\right\}} \\ {0.2951=\log \left\{0.9804+\frac{9.804 \times 10^{-4}}{C_{\mathrm{samp}}}\right\}}\end{array} \nonumber\]
and taking the inverse log of both sides gives
\[1.973=0.9804+\frac{9.804 \times 10^{-4}}{C_{\text {samp }}} \nonumber\]
Finally, solving for Csamp gives the concentration of Ca2+ as \(9.88 \times 10^{-4}\) M. Because we diluted the original sample of seawater by a factor of 10, the concentration of Ca2+ in the seawater sample is \(9.88 \times 10^{-3}\) M.
Free Ions Versus Complexed Ions
Most potentiometric electrodes are selective toward the free, uncomplexed form of the analyte, and do not respond to any of the analyte’s complexed forms. This selectivity provides potentiometric electrodes with a significant advantage over other quantitative methods of analysis if we need to determine the concentration of free ions. For example, calcium is present in urine both as free Ca2+ ions and as protein-bound Ca2+ ions. If we analyze a urine sample using atomic absorption spectroscopy, the signal is propor- tional to the total concentration of Ca2+ because both free and bound calcium are atomized. Analyzing urine with a Ca2+ ISE, however, gives a signal that is a function of only free Ca2+ ions because the protein-bound Ca2+ can not interact with the electrode’s membrane.
The best way to appreciate the theoretical and the practical details discussed in this section is to carefully examine a typical analytical method. Although each method is unique, the following description of the determination of F– in toothpaste provides an instructive example of a typical procedure. The description here is based on Kennedy, J. H. Analytical Chemistry— Practice, Harcourt Brace Jaovanovich: San Diego, 1984, p. 117–118.
Representative Method 11.2.1: Determination of Fluoride in Toothpaste
Description of the Method
The concentration of fluoride in toothpastes that contains soluble F– is determined with a F– ion-selective electrode using a calibration curve prepared with external standards. Although the F– ISE is very selective (only OH– with a KF–/OH– of 0.1 is a significant interferent), Fe3+ and Al3+ interfere with the analysis because they form soluble fluoride complexes that do not interact with the ion-selective electrode’s membrane. This interference is minimized by reacting any Fe3+ and Al3+ with a suitable complexing agent.
Procedure
Prepare 1 L of a standard solution of 1.00% w/v SnF2 and transfer it to a plastic bottle for storage. Using this solution, prepare 100 mL each of standards that contain 0.32%, 0.36%, 0.40%, 0.44% and 0.48% w/v SnF2, adding 400 mg of malic acid to each solution as a stabilizer. Transfer the standards to plastic bottles for storage. Prepare a total ionic strength adjustment buffer (TISAB) by mixing 500 mL of water, 57 mL of glacial acetic acid, 58 g of NaCl, and 4 g of disodium DCTA (trans-1,2-cyclohexanetetraacetic acid) in a 1-L beaker, stirring until dissolved. Cool the beaker in a water bath and add 5 M NaOH until the pH is between 5–5.5. Transfer the contents of the beaker to a 1-L volumetric flask and dilute to volume. Prepare each external standard by placing approximately 1 g of a fluoride-free toothpaste, 30 mL of distilled water, and 1.00 mL of standard into a 50-mL plastic beaker and mix vigorously for two min with a stir bar. Quantitatively transfer the resulting suspension to a 100-mL volumetric flask along with 50 mL of TISAB and dilute to volume with distilled water. Store the entire external standard in a 250-mL plastic beaker until you are ready to measure the potential. Prepare toothpaste samples by obtaining an approximately 1-g portion and treating in the same manner as the standards. Measure the cell potential for the external standards and the samples using a F– ion-selective electrode and an appropriate reference electrode. When measuring the potential, stir the solution and allow two to three minutes to reach a stable potential. Report the concentration of F– in the toothpaste %w/w SnF2.
Questions
1. The total ionic strength adjustment buffer serves several purposes in this procedure. Identify these purposes.
The composition of the TISAB has three purposes:
(a) The high concentration of NaCl (the final solutions are approximately 1 M NaCl) ensures that the ionic strength of each external standard and each sample is essentially identical. Because the activity coefficient for fluoride is the same in all solutions, we can write the Nernst equation in terms of fluoride’s concentration instead of its activity.
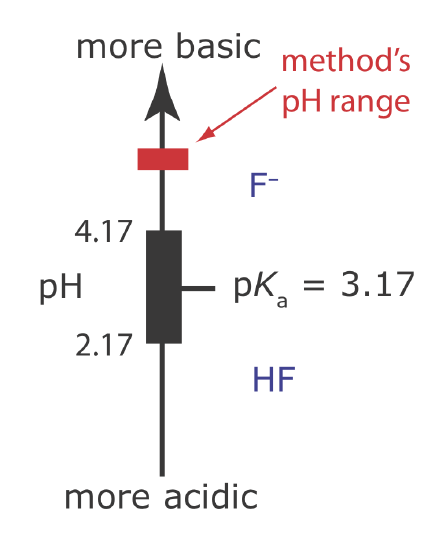
(b) The combination of glacial acetic acid and NaOH creates an acetic acid/acetate buffer of pH 5–5.5. As shown in Figure \(\PageIndex{17}\), the pH of this buffer is high enough to ensure that the predominate form of fluoride is F– instead of HF. This pH also is sufficiently acidic that it avoids an interference from OH– (see Example \(\PageIndex{8)}\)).
(c) DCTA is added as a complexing agent for Fe3+ or Al3+, preventing the formation of \(\text{FeF}_6^{3-}\) or \(\text{AlF}_6^{3-}\).
2. Why is a fluoride-free toothpaste added to the standard solutions?
Adding a fluoride-free toothpaste protects against any unaccounted for matrix effects that might influence the ion-selective electrode’s response. This assumes, of course, that the matrices of the two toothpastes are otherwise similar.
3. The procedure specifies that the standards and the sample should be stored in plastic containers. Why is it a bad idea to store the solutions in glass containers?
The fluoride ion is capable of reacting with glass to form SiF4.
4. Suppose your calibration curve has a slope of –57.98 mV for each 10-fold change in the concentration of F–. The ideal slope from the Nernst equation is –59.16 mV per 10-fold change in concentration. What effect does this have on the quantitative analysis for fluoride in toothpaste?
No effect at all! This is why we prepare a calibration curve using multiple standards.
Measurement of pH
With the availability of inexpensive glass pH electrodes and pH meters, the determination of pH is one of the most common quantitative analytical measurements. The potentiometric determination of pH, however, is not without complications, several of which we discuss in this section.
One complication is confusion over the meaning of pH [Kristensen, H. B.; Saloman, A.; Kokholm, G. Anal. Chem. 1991, 63, 885A–891A]. The conventional definition of pH in most general chemistry textbooks is
\[\mathrm{pH}=-\log \left[\mathrm{H}^{+}\right] \label{11.17}\]
As we now know, pH actually is a measure of the activity of H+.
\[\mathrm{pH}=-\log a_{\mathrm{H}^{+}} \label{11.18}\]
Try this experiment—find several general chemistry textbooks and look up pH in each textbook’s index. Turn to the appropriate pages and see how it is defined. Next, look up activity or activity coefficient in each textbook’s index and see if these terms are indexed.
Equation \ref{11.17} only approximates the true pH. If we calculate the pH of 0.1 M HCl using equation \ref{11.17}, we obtain a value of 1.00; the solution’s actual pH, as defined by equation \ref{11.18}, is 1.1 [Hawkes, S. J. J. Chem. Educ. 1994, 71, 747–749]. The activity and the concentration of H+ are not the same in 0.1 M HCl because the activity coefficient for H+ is not 1.00 in this matrix. Figure \(\PageIndex{18}\) shows a more colorful demonstration of the difference between activity and concentration.

A second complication in measuring pH is the uncertainty in the relationship between potential and activity. For a glass membrane electrode, the cell potential, (Ecell)samp, for a sample of unknown pH is
\[(E_{\text{cell}})_\text {samp} = K-\frac{R T}{F} \ln \frac{1}{a_{\mathrm{H}^{+}}}=K-\frac{2.303 R T}{F} \mathrm{pH}_{\mathrm{samp}} \label{11.19}\]
where K includes the potential of the reference electrode, the asymmetry potential of the glass membrane, and any junction potentials in the electrochemical cell. All the contributions to K are subject to uncertainty, and may change from day-to-day, as well as from electrode-to-electrode. For this reason, before using a pH electrode we calibrate it using a standard buffer of known pH. The cell potential for the standard, (Ecell)std, is
\[\left(E_{\text {ccll}}\right)_{\text {std}}=K-\frac{2.303 R T}{F} \mathrm{p} \mathrm{H}_{\mathrm{std}} \label{11.20}\]
where pHstd is the standard’s pH. Subtracting equation \ref{11.20} from equation \ref{11.19} and solving for pHsamp gives
\[\text{pH}_\text{samp} = \text{pH}_\text{std} - \frac{\left\{\left(E_{\text {cell}}\right)_{\text {samp}}-\left(E_{\text {cell}}\right)_{\text {std}}\right\} F}{2.303 R T} \label{11.21}\]
which is the operational definition of pH adopted by the International Union of Pure and Applied Chemistry [Covington, A. K.; Bates, R. B.; Durst, R. A. Pure & Appl. Chem. 1985, 57, 531–542].
Calibrating a pH electrode presents a third complication because we need a standard with an accurately known activity for H+. Table \(\PageIndex{6}\) provides pH values for several primary standard buffer solutions accepted by the National Institute of Standards and Technology.
To standardize a pH electrode using two buffers, choose one near a pH of 7 and one that is more acidic or basic depending on your sample’s expected pH. Rinse your pH electrode in deionized water, blot it dry with a laboratory wipe, and place it in the buffer with the pH closest to 7. Swirl the pH electrode and allow it to equilibrate until you obtain a stable reading. Adjust the “Standardize” or “Calibrate” knob until the meter displays the correct pH. Rinse and dry the electrode, and place it in the second buffer. After the electrode equilibrates, adjust the “Slope” or “Temperature” knob until the meter displays the correct pH.
Some pH meters can compensate for a change in temperature. To use this feature, place a temperature probe in the sample and connect it to the pH meter. Adjust the “Temperature” knob to the solution’s temperature and calibrate the pH meter using the “Calibrate” and “Slope” controls. As you are using the pH electrode, the pH meter compensates for any change in the sample’s temperature by adjusting the slope of the calibration curve using a Nernstian response of 2.303RT/F.
Clinical Applications
Because of their selectivity for analytes in complex matricies, ion-selective electrodes are important sensors for clinical samples. The most common analytes are electrolytes, such as Na+, K+, Ca2+, H+, and Cl–, and dissolved gases such as CO2. For extracellular fluids, such as blood and urine, the analysis can be made in vitro. An in situ analysis, however, requires a much smaller electrode that we can insert directly into a cell. Liquid-based membrane microelectrodes with tip diameters smaller than 1 μm are constructed by heating and drawing out a hard-glass capillary tube with an initial diameter of approximately 1–2 mm (Figure \(\PageIndex{19}\)). The microelectrode’s tip is made hydrophobic by dipping into a solution of dichlorodimethyl silane, and an inner solution appropriate for the analyte and a Ag/AgCl wire reference electrode are placed within the microelectrode. The microelectrode is dipped into a solution of the liquid complexing agent, which through capillary action draws a small volume of the liquid complexing agent into the tip. Potentiometric microelectrodes have been developed for a number of clinically important analytes, including H+, K+, Na+, Ca2+, Cl–, and I– [Bakker, E.; Pretsch, E. Trends Anal. Chem. 2008, 27, 612–618].
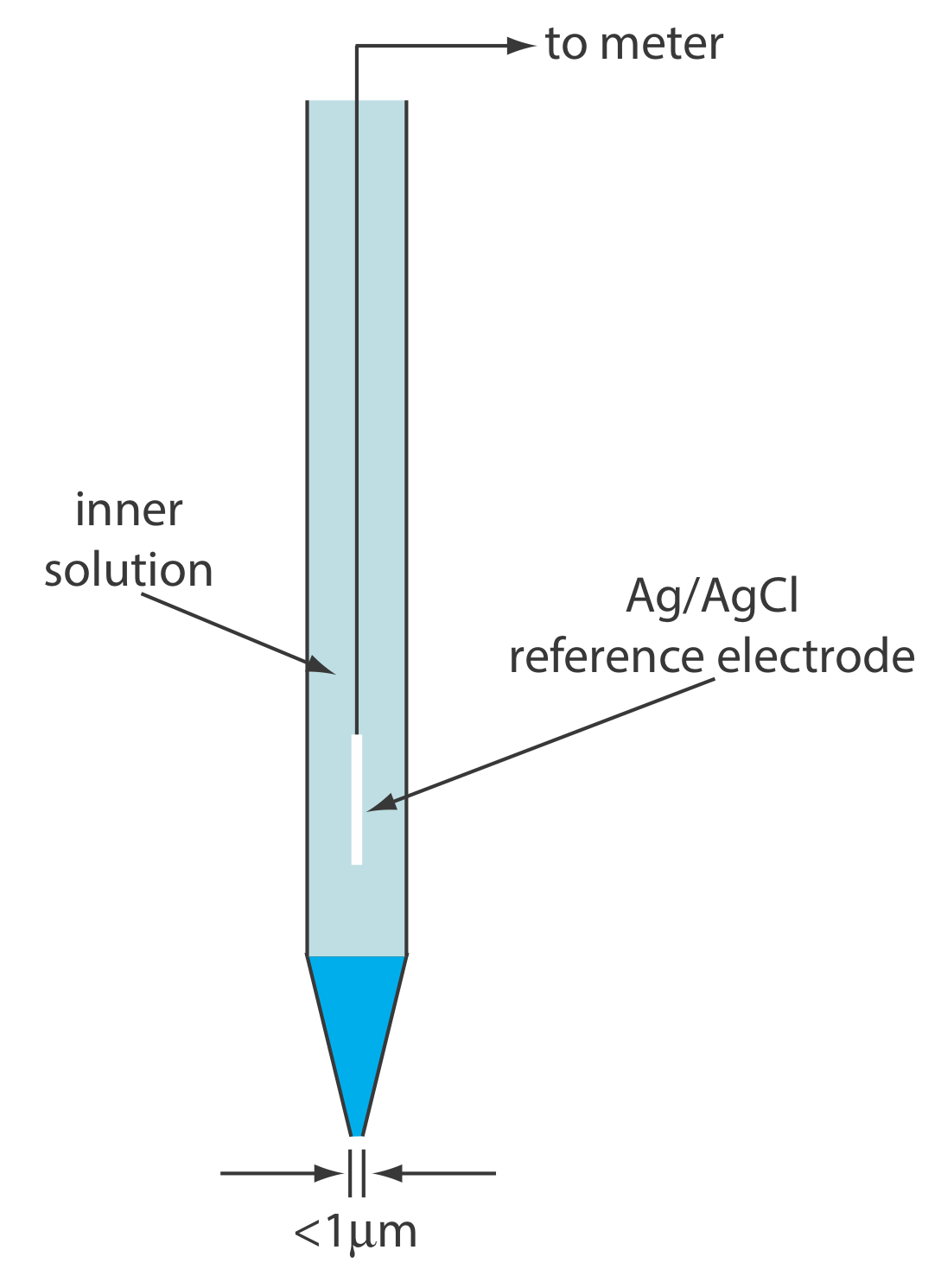
Environmental Applications
Although ion-selective electrodes are used in environmental analysis, their application is not as widespread as in clinical analysis. Although standard potentiometric methods are available for the analysis of CN–, F–, NH3, and \(\text{NO}_3^-\) in water and wastewater, other analytical methods generally provide better detection limits. One potential advantage of an ion-selective electrode is the ability to incorporate it into a flow cell for the continuous monitoring of wastewater streams.
Potentiometric Titrations
One method for determining the equivalence point of an acid–base titration is to use a pH electrode to monitor the change in pH during the titration. A potentiometric determination of the equivalence point is possible for acid–base, complexation, redox, and precipitation titrations, as well as for titrations in aqueous and nonaqueous solvents. Acid–base, complexation, and precipitation potentiometric titrations usually are monitored with an ion-selective electrode that responds the analyte, although an electrode that responds to the titrant or a reaction product also can be used. A redox electrode, such as a Pt wire, and a reference electrode are used for potentiometric redox titrations. More details about potentiometric titrations are found in Chapter 9.
Evaluation
Scale of Operation
The working range for most ion-selective electrodes is from a maximum concentration of 0.1–1 M to a minimum concentration of \(10^{-5}-10^{-11}\) M [(a) Bakker, E.; Pretsch, E. Anal. Chem. 2002, 74, 420A–426A; (b) Bakker, E.; Pretsch, E. Trends Anal. Chem. 2005, 24, 199–207]. This broad working range extends from major analytes to ultratrace analytes, and is significantly greater than many other analytical techniques. To use a conventional ion-selective electrode we need a minimum sample volume of several mL (a macro sample). Microelectrodes, such as the one shown in Figure \(\PageIndex{19}\), are used with an ultramicro sample, although care is needed to ensure that the sample is representative of the original sample.
Accuracy
The accuracy of a potentiometric analysis is limited by the error in measuring Ecell. Several factors contribute to this measurement error, including the contribution to the potential from interfering ions, the finite current that passes through the cell while we measure the potential, differences between the analyte’s activity coefficient in the samples and the standard solutions, and junction potentials. We can limit the effect of an interfering ion by including a separation step before the potentiometric analysis. Modern high impedance potentiometers minimize the amount of current that passes through the electrochemical cell. Finally, we can minimize the errors due to activity coefficients and junction potentials by matching the matrix of the standards to that of the sample. Even in the best circumstances, however, a difference of approximately ±1 mV for samples with equal concentrations of analyte is not unusual.
We can evaluate the effect of uncertainty on the accuracy of a potentiometric measurement by using a propagation of uncertainty. For a membrane ion-selective electrode the general expression for potential is
\[E_{\mathrm{cell}}=K+\frac{R T}{z F} \ln \left[ A\right] \nonumber\]
where z is the analyte’s, A, charge. From Table 4.3.1 in Chapter 4, the uncertainty in the cell potential, \(\Delta E_\text{cell}\) is
\[\triangle E_{\text {cell}}=\frac{R T}{z F} \times \frac{\Delta [A]}{[A]} \nonumber\]
Rearranging and multiplying through by 100 gives the percent relative error in concentration as
\[\% \text { relative error }=\frac{\Delta[A]}{[A]} \times 100=\frac{\triangle E_{\mathrm{cell}}}{R T / z F} \times 100 \label{11.22}\]
The relative error in concentration, therefore, is a function of the measurement error for the electrode’s potential, \(\Delta E_\text{cell}\), and the analyte’s charge. Table \(\PageIndex{7}\) provides representative values for ions with charges of ±1 and ±2 at a temperature of 25oC. Accuracies of 1–5% for monovalent ions and 2–10% for divalent ions are typical. Although equation \ref{11.22} applies to membrane electrodes, we can use if for a metallic electrode by replacing z with n.
Precision
Precision in potentiometry is limited by variations in temperature and the sensitivity of the potentiometer. Under most conditions—and when using a simple, general-purpose potentiometer—we can measure the potential with a repeatability of ±0.1 mV. Using Table \(\PageIndex{7}\), this corresponds to an uncertainty of ±0.4% for monovalent analytes and ±0.8% for divalent analytes. The reproducibility of potentiometric measurements is about a factor of ten poorer.
Sensitivity
The sensitivity of a potentiometric analysis is determined by the term RT/nF or RT/zF in the Nernst equation. Sensitivity is best for smaller values of n or z.
Selectivity
As described earlier, most ion-selective electrodes respond to more than one analyte; the selectivity for the analyte, however, often is significantly greater than the sensitivity for the interfering ions. The manufacturer of an ion-selective usually provides an ISE’s selectivity coefficients, which allows us to determine whether a potentiometric analysis is feasible for a given sample.
Time, Cost, and Equipment
In comparison to other techniques, potentiometry provides a rapid, relatively low-cost means for analyzing samples. The limiting factor when analyzing a large number of samples is the need to rinse the electrode between samples. The use of inexpensive, disposable ion-selective electrodes can increase a lab’s sample throughput. Figure \(\PageIndex{20}\) shows one example of a disposable ISE for Ag+ [Tymecki, L.; Zwierkowska, E.; Głąb, S.; Koncki, R. Sens. Actuators B 2003, 96, 482–488]. Commercial instruments for measuring pH or potential are available in a variety of price ranges, and includes portable models for use in the field.