2.2: Concentration
- Page ID
- 220655
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Concentration is a general measurement unit that reports the amount of solute present in a known amount of solution
\[\text{concentration} = \frac {\text{amount of solute}} {\text{amount of solution}} \label{2.1}\]
Although we associate the terms “solute” and “solution” with liquid samples, we can extend their use to gas-phase and solid-phase samples as well. Table \(\PageIndex{1}\) lists the most common units of concentration.
| Name | Units | Symbol |
|---|---|---|
| molarity | \(\frac {\text{moles solute}} {\text{liters solution}}\) | M |
| formality | \(\frac {\text{moles solute}} {\text{liters solution}}\) | F |
| normality | \(\frac {\text{equivalents solute}} {\text{liters solution}}\) | N |
| molality | \(\frac {\text{moles solute}} {\text{kilograms solvent}}\) | m |
| weight percent | \(\frac {\text{grams solute}} {\text{100 grams solution}}\) | % w/w |
| volume percent | \(\frac {\text{mL solute}} {\text{100 mL solution}}\) | % v/v |
| weight-to-volume percent | \(\frac {\text{grams solute}} {\text{100 mL solution}}\) | % w/v |
| parts per million | \(\frac {\text{grams solute}} {10^6 \text{ grams solution}}\) | ppm |
| parts per billion | \(\frac {\text{grams solute}} {10^9 \text{ grams solution}}\) | ppb |
An alternative expression for weight percent is
\[\frac {\text{grams solute}} {\text{grams solution}} \times 100\ \nonumber\]
You can use similar alternative expressions for volume percent and for weight-to-volume percent.
Molarity and Formality
Both molarity and formality express concentration as moles of solute per liter of solution; however, there is a subtle difference between them. Molarity is the concentration of a particular chemical species. Formality, on the other hand, is a substance’s total concentration without regard to its specific chemical form. There is no difference between a compound’s molarity and formality if it dissolves without dissociating into ions. The formal concentration of a solution of glucose, for example, is the same as its molarity.
For a compound that ionizes in solution, such as CaCl2, molarity and formality are different. When we dissolve 0.1 moles of CaCl2 in 1 L of water, the solution contains 0.1 moles of Ca2+ and 0.2 moles of Cl–. The molarity of CaCl2, therefore, is zero since there is no undissociated CaCl2 in solution; instead, the solution is 0.1 M in Ca2+ and 0.2 M in Cl–. The formality of CaCl2, however, is 0.1 F since it represents the total amount of CaCl2 in solution. This more rigorous definition of molarity, for better or worse, largely is ignored in the current literature, as it is in this textbook. When we state that a solution is 0.1 M CaCl2 we understand it to consist of Ca2+ and Cl– ions. We will reserve the unit of formality to situations where it provides a clearer description of solution chemistry.
Molarity is used so frequently that we use a symbolic notation to simplify its expression in equations and in writing. Square brackets around a species indicate that we are referring to that species’ molarity. Thus, [Ca2+] is read as “the molarity of calcium ions.”
For a solute that dissolves without undergoing ionization, molarity and formality have the same value. A solution that is 0.0259 M in glucose, for example, is 0.0259 F in glucose as well.
Normality
Normality is a concentration unit that no longer is in common use; however, because you may encounter normality in older handbooks of analytical methods, it is helpful to understand its meaning. Normality defines concentration in terms of an equivalent, which is the amount of one chemical species that reacts stoichiometrically with another chemical species. Note that this definition makes an equivalent, and thus normality, a function of the chemical reaction in which the species participates. Although a solution of H2SO4 has a fixed molarity, its normality depends on how it reacts. You will find a more detailed treatment of normality in Appendix 1.
One handbook that still uses normality is Standard Methods for the Examination of Water and Wastewater, a joint publication of the American Public Health Association, the American Water Works Association, and the Water Environment Federation. This handbook is one of the primary resources for the environmental analysis of water and wastewater.
Molality
Molality is used in thermodynamic calculations where a temperature independent unit of concentration is needed. Molarity is based on the volume of solution that contains the solute. Since density is a temperature dependent property, a solution’s volume, and thus its molar concentration, changes with temperature. By using the solvent’s mass in place of the solution’s volume, the resulting concentration becomes independent of temperature.
Weight, Volume, and Weight-to-Volume Percent
Weight percent (% w/w), volume percent (% v/v) and weight-to-volume percent (% w/v) express concentration as the units of solute present in 100 units of solution. A solution that is 1.5% w/v NH4NO3, for example, contains 1.5 gram of NH4NO3 in 100 mL of solution.
Parts Per Million and Parts Per Billion
Parts per million (ppm) and parts per billion (ppb) are ratios that give the grams of solute in, respectively, one million or one billion grams of sample. For example, a sample of steel that is 450 ppm in Mn contains 450 μg of Mn for every gram of steel. If we approximate the density of an aqueous solution as 1.00 g/mL, then we can express solution concentrations in ppm or ppb using the following relationships.
\[\text{ppm} = \frac {\mu \text{g}} {\text{g}} = \frac {\text{mg}} {\text{L}} = \frac {\mu \text{g}} {\text{mL}} \quad \text{ppb} = \frac {\text{ng}} {\text{g}} = \frac {\mu \text{g}} {\text{L}} = \frac {\text{ng}} {\text{mL}} \nonumber\]
For gases a part per million usually is expressed as a volume ratio; for example, a helium concentration of 6.3 ppm means that one liter of air contains 6.3 μL of He.
You should be careful when using parts per million and parts per billion to express the concentration of an aqueous solute. The difference between a solute’s concentration in mg/L and ng/g, for example, is significant if the solution’s density is not 1.00 g/mL. For this reason many organizations advise against using the abbreviation ppm and ppb (see section 7.10.3 at www.nist.gov). If in doubt, include the exact units, such as 0.53 μg Pb2+/L for the concentration of lead in a sample of seawater.
Converting Between Concentration Units
The most common ways to express concentration in analytical chemistry are molarity, weight percent, volume percent, weight-to-volume percent, parts per million and parts per billion. The general definition of concentration in Equation \ref{2.1} makes it is easy to convert between concentration units.
A concentrated solution of ammonia is 28.0% w/w NH3 and has a density of 0.899 g/mL. What is the molar concentration of NH3 in this solution?
Solution
\[\frac {28.0 \text{ g } \ce{NH3}} {100 \text{ g soln}} \times \frac {0.899 \text{ g soln}} {\text{ml soln}} \times \frac {1 \text{ mol } \ce{NH3}} {17.03 \text{ g } \ce{NH3}} \times \frac {1000 \text{mL}} {\text{L}} = 14.8 \text{ M} \nonumber\]
The maximum permissible concentration of chloride ion in a municipal drinking water supply is \(2.50 \times 10^2\) ppm Cl–. When the supply of water exceeds this limit it often has a distinctive salty taste. What is the equivalent molar concentration of Cl–?
Solution
\[\frac {2.50 \times 10^2 \text{ mg } \ce{Cl-}} {\text{L}} \times \frac {1 \text{ g}} {1000 \text{ mg}} \times \frac {1 \text{ mol } \ce{Cl-}} {35.453 \text{ g} \ce{Cl-}} = 7.05 \times 10^{-3} \text{ M} \nonumber\]
Which solution—0.50 M NaCl or 0.25 M SrCl2—has the larger concentration when expressed in mg/mL?
- Answer
-
The concentrations of the two solutions are
\[\frac {0.50 \text{ mol NaCl}} {\text{L}} \times \frac {58.44 \text{ g NaCl}} {\text{mol NaCl}} \times \frac {10^6 \: \mu \text{g}} {\text{g}} \times \frac {1 \text{L}} {1000 \text{ mL}} = 2.9 \times 10^{4} \: \mu \text{g/mL NaCl} \nonumber\]
\[\frac {0.25 \text{ mol } \ce{SrCl2}} {\text{L}} \times \frac {158.5 \text{ g } \ce{SrCl2}} {\text{mol } \ce{SrCl2}} \times \frac {10^6 \: \mu \text{g}} {\text{g}} \times \frac {1 \text{L}} {1000 \text{ mL}} = 4.0 \times 10^{4} \: \mu \text{g/ml } \ce{SrCl2} \nonumber\]
The solution of SrCl2 has the larger concentration when it is expressed in μg/mL instead of in mol/L.
p-Functions
Sometimes it is inconvenient to use the concentration units in Table \(\PageIndex{1}\). For example, during a chemical reaction a species’ concentration may change by many orders of magnitude. If we want to display the reaction’s progress graphically we might wish to plot the reactant’s concentration as a function of the volume of a reagent added to the reaction. Such is the case in Figure \(\PageIndex{1}\) for the titration of HCl with NaOH. The y-axis on the left-side of the figure displays the [H+] as a function of the volume of NaOH. The initial [H+] is 0.10 M and its concentration after adding 80 mL of NaOH is \(4.3 \times 10^{-13}\) M. We easily can follow the change in [H+] for the addition of the first 50 mL of NaOH; however, for the remaining volumes of NaOH the change in [H+] is too small to see.
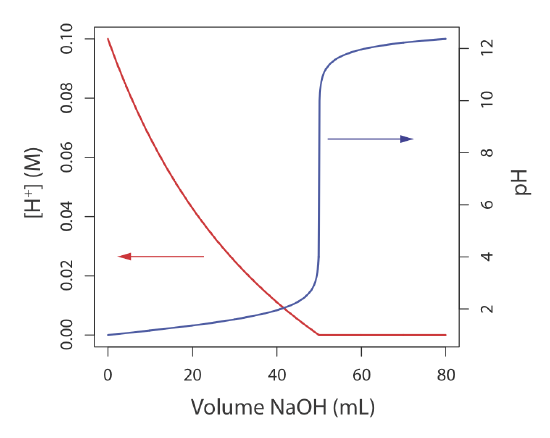
When working with concentrations that span many orders of magnitude, it often is more convenient to express concentration using a p-function. The p-function of X is written as pX and is defined as
\[\text{p} X = - \log (X) \nonumber\]
The pH of a solution that is 0.10 M H+ for example, is
\[\text{pH} = - \log [\ce{H+}] = - \log (0.10) = 1.00 \nonumber\]
and the pH of \(4.3 \times 10^{-13}\) M H+ is
\[\text{pH} = - \log [\ce{H+}] = - \log (4.3 \times 10^{-13}) = 12.37 \nonumber\]
Figure \(\PageIndex{1}\) shows that plotting pH as a function of the volume of NaOH provides more useful information about how the concentration of H+ changes during the titration.
A more appropriate equation for pH is \(\text{pH} = - \log (a_{\ce{H+}})\) where \(a_{\ce{H+}}\) is the activity of the hydrogen ion. See Chapter 6.9 for more details. For now the approximate equation \(\text{pH} = - \log [\ce{H+}]\) is sufficient.
What is pNa for a solution of \(1.76 \times 10^{-3}\) M Na3PO4?
Solution
Since each mole of Na3PO4 contains three moles of Na+, the concentration of Na+ is
\[[\ce{Na+}] = (1.76 \times 10^{-3} \text{ M}) \times \frac {3 \text{ mol } \ce{Na+}} {\text{mol } \ce{Na3PO4}} = 5.28 \times 10^{-3} \text{ M} \nonumber\]
and pNa is
\[\text{pNa} = - \log [\ce{Na+}] = - \log (5.28 \times 10^{-3}) = 2.277 \nonumber\]
Remember that a pNa of 2.777 has three, not four, significant figures; the 2 that appears in the one’s place indicates the power of 10 when we write [Na+] as \(0.528 \times 10^{-2}\) M.
What is the [H+] in a solution that has a pH of 5.16?
Solution
The concentration of H+ is
\[\text{pH} = - \log [\ce{H+}] = 5.16 \nonumber\]
\[\log [\ce{H+}] = -5.16 \nonumber\]
\[[\ce{H+}] = 10^{-5.16} = 6.9 \times 10^{-6} \text{ M} \nonumber\]
Recall that if log(X) = a, then X = 10a.
What are the values for pNa and pSO4 if we dissolve 1.5 g Na2SO4 in a total solution volume of 500.0 mL?
- Answer
-
The concentrations of Na+ and \(\ce{SO4^{2-}}\) are
\[\frac {1.5 \text{ g } \ce{Na2SO4}} {0.500 \text{L}} \times \frac {1 \text{ mol } \ce{Na2SO4}} {142.0 \text{ g } \ce{Na2SO4}} \times \frac {2 \text{ mol } \ce{Na+}} {\text{mol } \ce{mol } \ce{Na2SO4}} = 4.23 \times 10^{-2} \text{ M } \ce{Na+} \nonumber\]
\[\frac {1.5 \text{ g } \ce{Na2SO4}} {0.500 \text{L}} \times \frac {1 \text{ mol } \ce{Na2SO4}} {142.0 \text{ g } \ce{Na2SO4}} \times \frac {1 \text{ mol } \ce{SO4^{2-}}} {\text{mol } \ce{mol } \ce{Na2SO4}} = 2.11 \times 10^{-2} \text{ M } \ce{SO4^{2-}} \nonumber\]
The pNa and pSO4 values are
\[\text{pNa} = - \log (4.23 \times 10^{-2} \text{ M } \ce{Na+}) = 1.37 \nonumber\]
\[\text{pSO}_4 = - \log (2.11 \times 10^{-2} \text{ M } \ce{SO4^{2-}}) = 1.68 \nonumber\]


