25.4 Configurations of Aldoses
- Page ID
- 91045
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- draw the structures of all possible aldotetroses, aldopentoses, and aldohexoses, without necessarily being able to assign names to the individual compounds.
- draw the Fischer projection of D‑glyceraldehyde, D‑ribose and D‑glucose from memory.
The four chiral centers in glucose indicate there may be as many as sixteen (24) stereoisomers having this constitution. These would exist as eight diastereomeric pairs of enantiomers, and the initial challenge was to determine which of the eight corresponded to glucose. This challenge was accepted and met in 1891 by the German chemist Emil Fischer. His successful negotiation of the stereochemical maze presented by the aldohexoses was a logical tour de force, and it is fitting that he received the 1902 Nobel Prize for chemistry for this accomplishment. One of the first tasks faced by Fischer was to devise a method of representing the configuration of each chiral center in an unambiguous manner. To this end, he invented a simple technique for drawing chains of chiral centers, that we now call the Fischer projection formula.
At the time Fischer undertook the glucose project it was not possible to establish the absolute configuration of an enantiomer. Consequently, Fischer made an arbitrary choice for (+)-glucose and established a network of related aldose configurations that he called the D-family. The mirror images of these configurations were then designated the L-family of aldoses. To illustrate using present day knowledge, Fischer projection formulas and names for the D-aldose family (three to six-carbon atoms) are shown below, with the asymmetric carbon atoms (chiral centers) colored red.
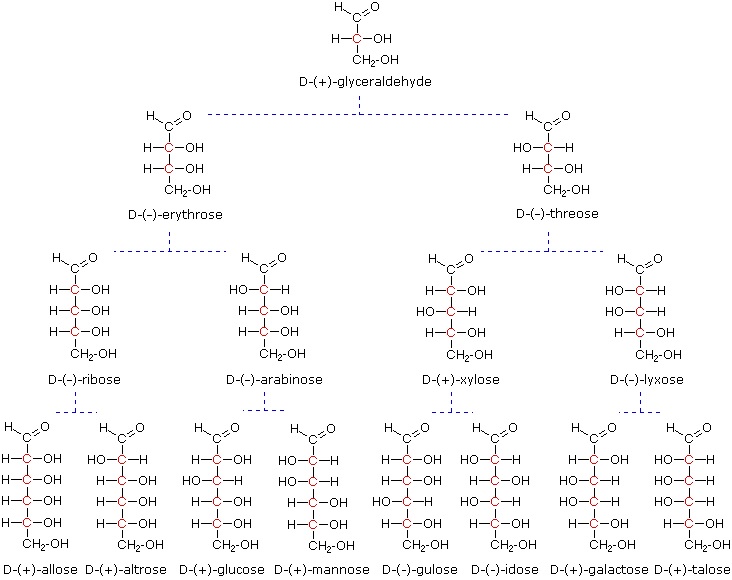
The last chiral center in an aldose chain (farthest from the aldehyde group) was chosen by Fischer as the D / L designator site. If the hydroxyl group in the projection formula pointed to the right, it was defined as a member of the D-family. A left directed hydroxyl group (the mirror image) then represented the L-family. Fischer's initial assignment of the D-configuration had a 50:50 chance of being right, but all his subsequent conclusions concerning the relative configurations of various aldoses were soundly based. In 1951 x-ray fluorescence studies of (+)-tartaric acid, carried out in the Netherlands by Johannes Martin Bijvoet (pronounced "buy foot"), proved that Fischer's choice was correct.
It is important to recognize that the sign of a compound's specific rotation (an experimental number) does not correlate with its configuration (D or L). It is a simple matter to measure an optical rotation with a polarimeter. Determining an absolute configuration usually requires chemical interconversion with known compounds by stereospecific reaction paths.
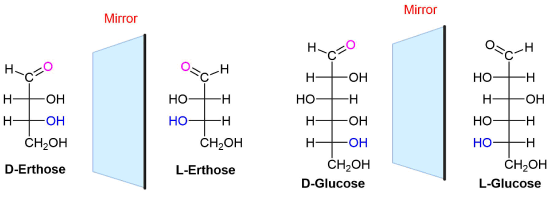
Draw the Fisher projection of L-erythrose and L-Glucose
Solution
Use the Fischer projection provided above and reverse all of the chiral centers to provide the L-sugar. Note that in both cases the D sugars have the OH going to the right on the chiral center furthest away from the carbonyl. The L-sugars have the OH going to the left.
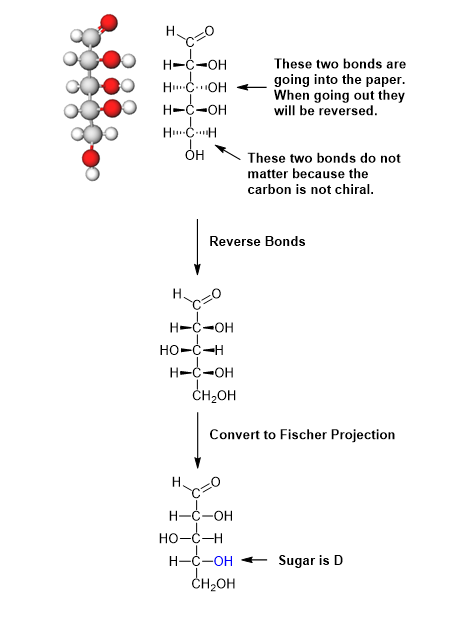
Please draw the Fischer projection fo the following aldopentose and determine if the sugars is D or L.
Solution
First, rotate the model so that the carbonyl is at the top. This is requirement of a Fischer projection. Next rotate the model so that the H and OH of the chiral carbon just below the carbonyl are facing towards you. In this orientation, a dash/wedge model will have every other set of bonds going into the plane of the page. This is not the correct orientation of a Fischer project so they must be modified. The H and OH bonds need to be coming out of the plane of the page in a Fisher projects. When converting bonds from going into the page to going out of the page the orientation of the H and OH are reversed. Remember that the last -CH2OH of a sugar is achiral so the orientation does not need to be shown. Once the bonds are oriented correctly the wedge bonds can be converted to those of a Fischer projection.
Exercises
For the following model of a sugar, please draw its Fischer projection and name it.
- Answer
-
D-Mannose
How many heptose stereoisomers would there expected to be? How many would be D-Sugars?
- Answer
-
There would be 25 = 32 heptose stereoisomers. Half of these would be D-sugars or 16.
Draw the Fischer projection of the following sugars.
- L-Ribose
- L-Galactose
- L-Talose
- Answer
-
a)
b)
c)
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

