25.5 Cyclic Structures of Monosaccharides: Anomers
- Page ID
- 91046
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- determine whether a given monosaccharide will exist as a pyranose or furanose.
- draw the cyclic pyranose form of a monosaccharide, given its Fischer projection.
- draw the Fischer projection of a monosaccharide, given its cyclic pyranose form.
- draw, from memory, the cyclic pyranose form of D‑glucose.
- determine whether a given cyclic pyranose form represents the D or L form of the monosaccharide concerned.
- describe the phenomenon known as mutarotation.
- explain, through the use of chemical equations, exactly what happens at the molecular level during the mutarotation process.
Make certain that you can define, and use in context, the key terms below.
- alpha anomer
- anomer
- anomeric centre
- beta anomer
- furanose
- mutarotation
- pyranose
If necessary, before you attempt to study this section, review the formation of hemiacetals discussed in Section 19.10.
As noted above, the preferred structural form of many monosaccharides may be that of a cyclic hemiacetal. Five and six-membered rings are favored over other ring sizes because of their low angle and eclipsing strain. Cyclic structures of this kind are termed furanose (five-membered) or pyranose (six-membered), reflecting the ring size relationship to the common heterocyclic compounds furan and pyran shown on the right. Ribose, an important aldopentose, commonly adopts a furanose structure, as shown in the following illustration. By convention for the D-family, the five-membered furanose ring is drawn in an edgewise projection with the ring oxygen positioned away from the viewer. The anomeric carbon atom (colored red here) is placed on the right. The upper bond to this carbon is defined as beta, the lower bond then is alpha.

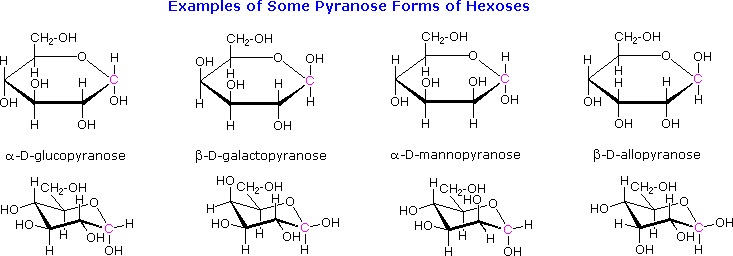
The cyclic pyranose forms of various monosaccharides are often drawn in a flat projection known as a Haworth formula, after the British chemist, Norman Haworth. As with the furanose ring, the anomeric carbon is placed on the right with the ring oxygen to the back of the edgewise view. In the D-family, the alpha and beta bonds have the same orientation defined for the furanose ring (beta is up & alpha is down). These Haworth formulas are convenient for displaying stereochemical relationships, but do not represent the true shape of the molecules. We know that these molecules are actually puckered in a fashion we call a chair conformation. Examples of four typical pyranose structures are shown below, both as Haworth projections and as the more representative chair conformers. The anomeric carbons are colored red.
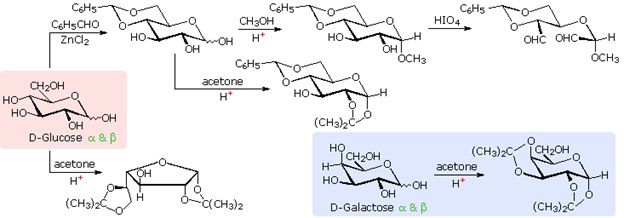
The size of the cyclic hemiacetal ring adopted by a given sugar is not constant, but may vary with substituents and other structural features. Aldolhexoses usually form pyranose rings and their pentose homologs tend to prefer the furanose form, but there are many counter examples. The formation of acetal derivatives illustrates how subtle changes may alter this selectivity. A pyranose structure for D-glucose is drawn in the rose-shaded box on the left. Acetal derivatives have been prepared by acid-catalyzed reactions with benzaldehyde and acetone. As a rule, benzaldehyde forms six-membered cyclic acetals, whereas acetone prefers to form five-membered acetals. The top equation shows the formation and some reactions of the 4,6-O-benzylidene acetal, a commonly employed protective group. A methyl glycoside derivative of this compound (see below) leaves the C-2 and C-3 hydroxyl groups exposed to reactions such as the periodic acid cleavage, shown as the last step. The formation of an isopropylidene acetal at C-1 and C-2, center structure, leaves the C-3 hydroxyl as the only unprotected function. Selective oxidation to a ketone is then possible. Finally, direct di-O-isopropylidene derivatization of glucose by reaction with excess acetone results in a change to a furanose structure in which the C-3 hydroxyl is again unprotected. However, the same reaction with D-galactose, shown in the blue-shaded box, produces a pyranose product in which the C-6 hydroxyl is unprotected. Both derivatives do not react with Tollens' reagent. This difference in behavior is attributed to the cis-orientation of the C-3 and C-4 hydroxyl groups in galactose, which permits formation of a less strained five-membered cyclic acetal, compared with the trans-C-3 and C-4 hydroxyl groups in glucose. Derivatizations of this kind permit selective reactions to be conducted at different locations in these highly functionalized molecules.
Anomers of Simple Sugars: Mutarotation of Glucose
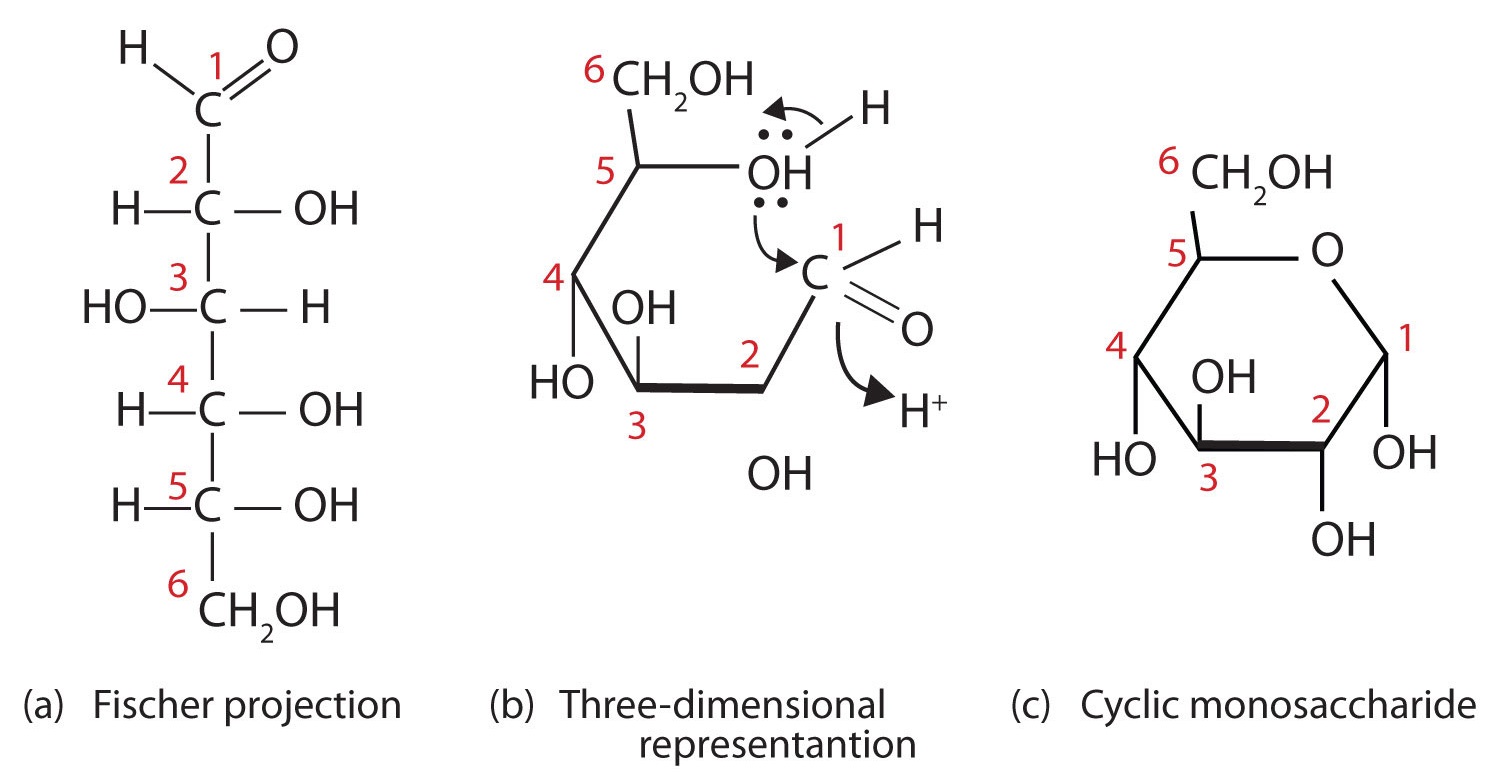
Figure 1: Cyclization of D-Glucose. D-Glucose can be represented with a Fischer projection (a) or three dimensionally (b). By reacting the OH group on the fifth carbon atom with the aldehyde group, the cyclic monosaccharide (c) is produced.
When a straight-chain monosaccharide, such as any of the structures shown in Figure 1, forms a cyclic structure, the carbonyl oxygen atom may be pushed either up or down, giving rise to two stereoisomers, as shown in Figure 2. The structure shown on the left side of Figure 2, with the OH group on the first carbon atom projected downward, represent what is called the alpha (α) form. The structures on the right side, with the OH group on the first carbon atom pointed upward, is the beta (β) form. These two stereoisomers of a cyclic monosaccharide are known as anomers; they differ in structure around the anomeric carbon—that is, the carbon atom that was the carbonyl carbon atom in the straight-chain form.
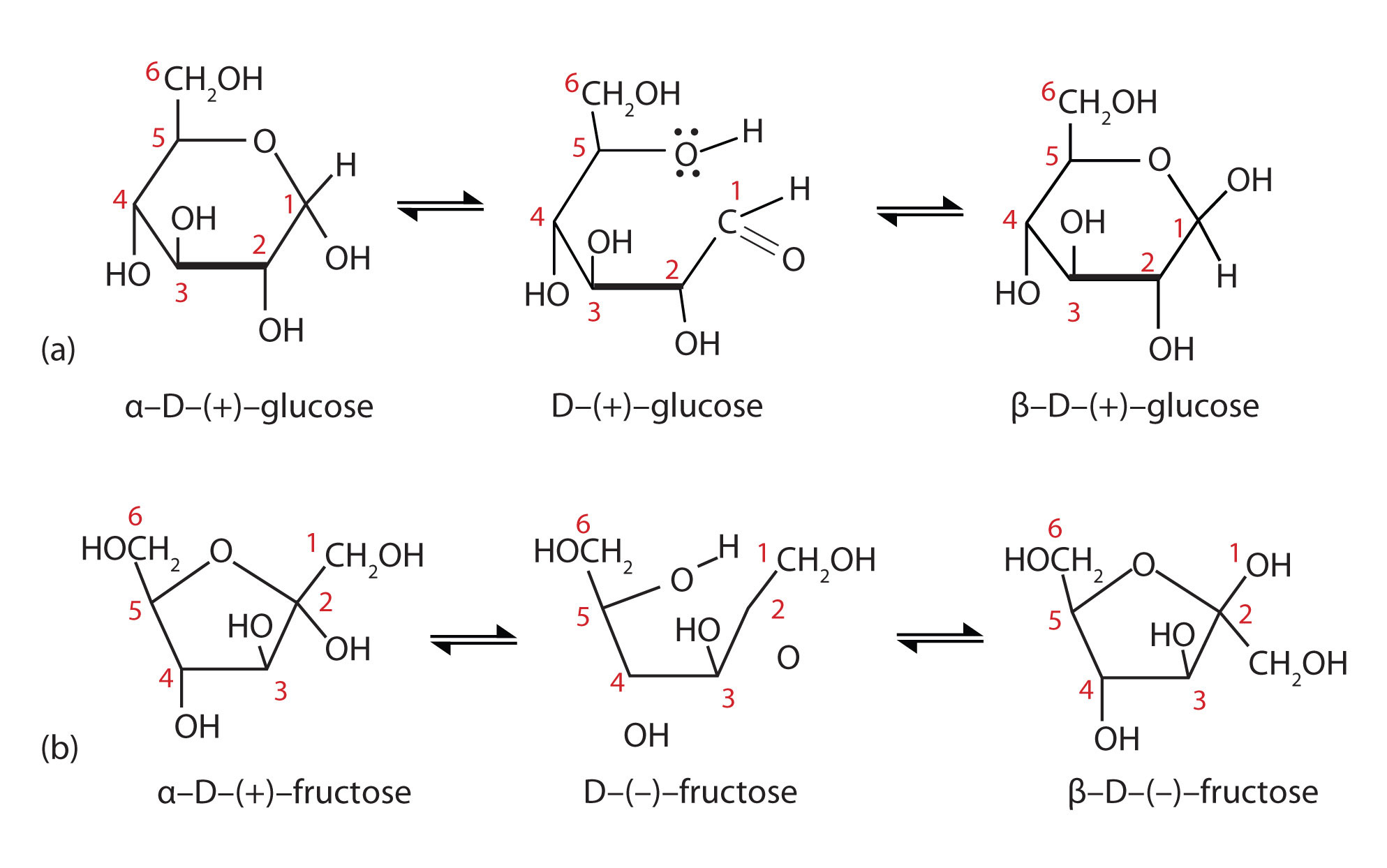
Figure 2: Monosaccharides. In an aqueous solution, monosaccharides exist as an equilibrium mixture of three forms. The interconversion between the forms is known as mutarotation, which is shown for D-glucose (a) and D-fructose (b).
It is possible to obtain a sample of crystalline glucose in which all the molecules have the α structure or all have the β structure. The α form melts at 146°C and has a specific rotation of +112°, while the β form melts at 150°C and has a specific rotation of +18.7°. When the sample is dissolved in water, however, a mixture is soon produced containing both anomers as well as the straight-chain form, in dynamic equilibrium (part (a) of Figure 2). You can start with a pure crystalline sample of glucose consisting entirely of either anomer, but as soon as the molecules dissolve in water, they open to form the carbonyl group and then reclose to form either the α or the β anomer. The opening and closing repeats continuously in an ongoing interconversion between anomeric forms and is referred to as mutarotation (Latin mutare, meaning “to change”). At equilibrium, the mixture consists of about 36% α-D-glucose, 64% β-D-glucose, and less than 0.02% of the open-chain aldehyde form. The observed rotation of this solution is +52.7°.
Even though only a small percentage of the molecules are in the open-chain aldehyde form at any time, the solution will nevertheless exhibit the characteristic reactions of an aldehyde. As the small amount of free aldehyde is used up in a reaction, there is a shift in the equilibrium to yield more aldehyde. Thus, all the molecules may eventually react, even though very little free aldehyde is present at a time.
Commonly, (e.g., in Figures 1 and 2) the cyclic forms of sugars are depicted using a convention first suggested by Walter N. Haworth, an English chemist. The molecules are drawn as planar hexagons with a darkened edge representing the side facing toward the viewer. The structure is simplified to show only the functional groups attached to the carbon atoms. Any group written to the right in a Fischer projection appears below the plane of the ring in a Haworth projection, and any group written to the left in a Fischer projection appears above the plane in a Haworth projection.
The difference between the α and the β forms of sugars may seem trivial, but such structural differences are often crucial in biochemical reactions. This explains why we can get energy from the starch in potatoes and other plants but not from cellulose, even though both starch and cellulose are polysaccharides composed of glucose molecules linked together.
Summary
Monosaccharides that contain five or more carbons atoms form cyclic structures in aqueous solution. Two cyclic stereoisomers can form from each straight-chain monosaccharide; these are known as anomers. In an aqueous solution, an equilibrium mixture forms between the two anomers and the straight-chain structure of a monosaccharide in a process known as mutarotation.
Exercises
Draw the following in their most stable chair conformation:
- Answer
-
Because the both have two axial OH's their chair conformations should be roughly the same stability.
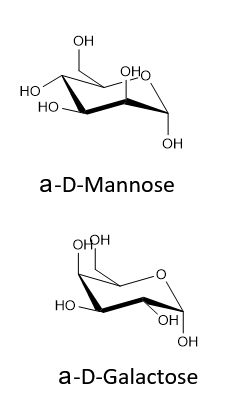
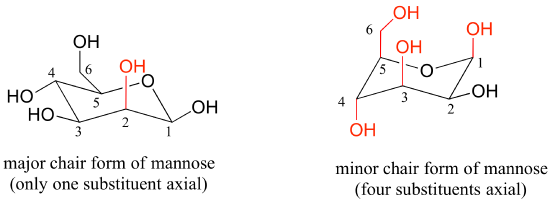
Draw the two chair conformations of the sugar called mannose, being sure to clearly show each non-hydrogen substituent as axial or equatorial. Predict which conformation is likely to be more stable, and explain why.
- Answer
-
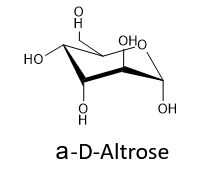
Draw the cyclic structure of α-D-altrose.
- Answer
-
Draw the cyclic structure for β-D-galactose. Identify the anomeric carbon.
- Answer
-
.png?revision=1&size=bestfit&width=309&height=175)
To identify the structure, we should first start with the Fischer projection of D-galactose. Since it is an aldohexose, we will start with the pyranose ring. The beta anomer was requested, so the OH on the anomeric carbon (C1) is cis to C6. Since C6 is top face (pointing up), the OH will be top face. Carbons 2, 3, and 4 are then arranged based on the Fischer projection arrangement at those carbons (C2 right, C3 left, and C4 left).
Given that the aldohexose D-mannose differs from D-glucose only in the configuration at the second carbon atom, draw the cyclic structure for α-D-mannose.
- Answer
-
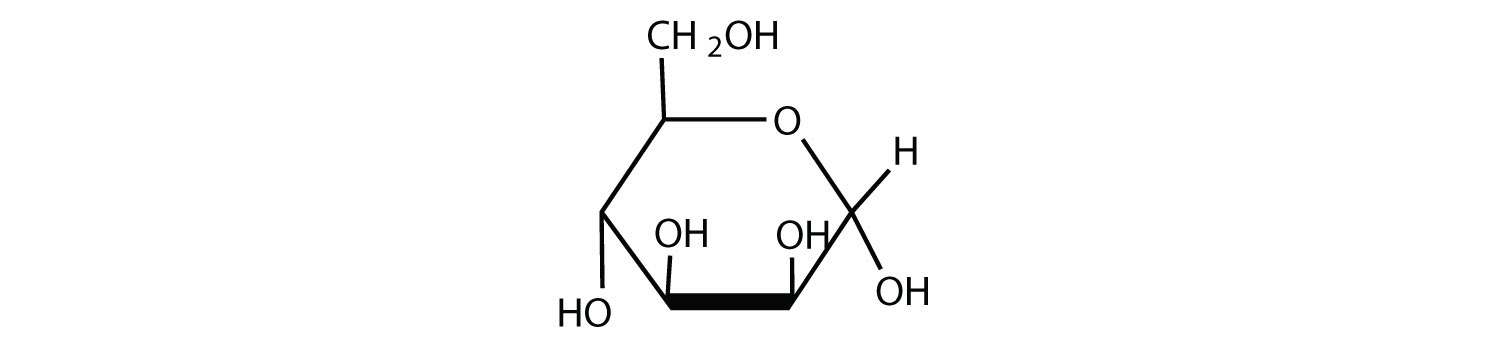
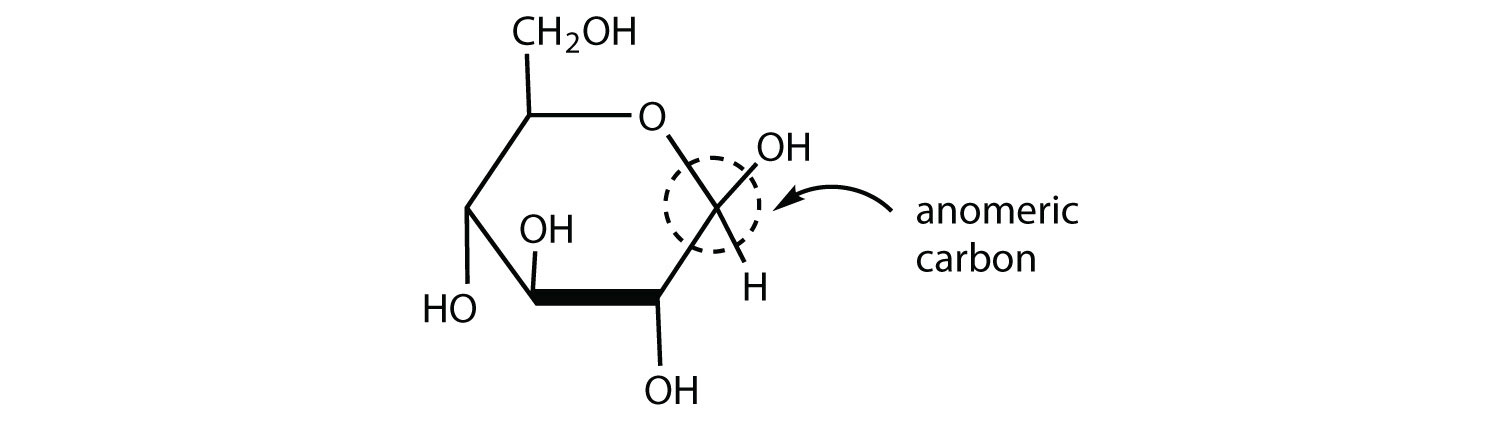
Draw the cyclic structure for β-D-glucose. Identify the anomeric carbon.
- Answer
-
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
- The Basics of General, Organic, and Biological Chemistry by David W. Ball, John W. Hill, and Rhonda J. Scott.

