25.3 D, L Sugars
- Page ID
- 91044
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- identify a specific enantioner of a monosaccharide as being D or L, given its Fischer projection.
- identify the limitations of the D, L system of nomenclature for carbohydrates.
- assign an R or S configuration to each of the chiral carbon atoms present in a monosaccharide, given its Fischer projection.
- draw the Fischer projection formula for a monosaccharide, given its systematic name, complete with the configuration of each chiral carbon atom.
- construct a molecular model of a monosaccharide, given its systematic name, complete with the configuration of each chiral carbon atom.
Make certain that you can define, and use in context, the key terms below.
- D sugar
- L sugar
If you find that you have forgotten the meanings of terms such as dextrorotatory and polarimeter, refer back to Section 5.3 in which the fundamentals of optical activity were introduced.
How would you set about the task of deciding whether each chiral carbon has an R or an S configuration? True, you could use molecular models, but suppose that a model set had not been available—what would you have done then?
One approach is to focus on the carbon atom of interest and sketch a three-dimensional representation of the configuration around that atom, remembering the convention used in Fischer projections: vertical lines represent bonds going into the page, and horizontal lines represent bonds coming out of the page. Thus, the configuration around carbon atom 2 in structure a can be represented as follows:
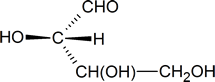
In your mind, you should be able to imagine how this molecule would look if it was rotated so that the bonds that are shown as coming out of the page are now in the plane of the page. [One possible way of doing this is to try and imagine how the molecule would look if it was viewed from a point at the bottom of the page.] What you should see in your mind is a representation similar to the one drawn below.
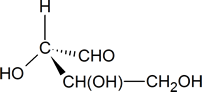
To determine whether the configuration about the central carbon atom is R or S, we must rotate the molecule so that the group with the lowest priority (H), is directed away from the viewer. This effect can be achieved by keeping the hydroxyl group in its present position and moving each of the other three groups one position clockwise.
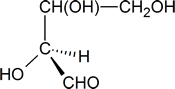
The Cahn-Ingold-Prelog order of priority for the three remaining groups is OH > CHO > CH(OH)CH2OH; thus, we see that we could trace out a counterclockwise path going from the highest-priority group to the second- and third-highest, and we conclude that the central carbon atom has an S configuration.
The Configuration of Glucose
The four chiral centers in glucose indicate there may be as many as sixteen (24) stereoisomers having this constitution. These would exist as eight diastereomeric pairs of enantiomers, and the initial challenge was to determine which of the eight corresponded to glucose. This challenge was accepted and met in 1891 by the German chemist Emil Fischer. His successful negotiation of the stereochemical maze presented by the aldohexoses was a logical tour de force, and it is fitting that he received the 1902 Nobel Prize for chemistry for this accomplishment. One of the first tasks faced by Fischer was to devise a method of representing the configuration of each chiral center in an unambiguous manner. To this end, he invented a simple technique for drawing chains of chiral centers, that we now call the Fischer projection formula. Click on this link for a review.
At the time Fischer undertook the glucose project it was not possible to establish the absolute configuration of an enantiomer. Consequently, Fischer made an arbitrary choice for (+)-glucose and established a network of related aldose configurations that he called the D-family. The mirror images of these configurations were then designated the L-family of aldoses. To illustrate using present day knowledge, Fischer projection formulas and names for the D-aldose family (three to six-carbon atoms) are shown below, with the asymmetric carbon atoms (chiral centers) colored red. The last chiral center in an aldose chain (farthest from the aldehyde group) was chosen by Fischer as the D / L designator site. If the hydroxyl group in the projection formula pointed to the right, it was defined as a member of the D-family. A left directed hydroxyl group (the mirror image) then represented the L-family. Fischer's initial assignment of the D-configuration had a 50:50 chance of being right, but all his subsequent conclusions concerning the relative configurations of various aldoses were soundly based. In 1951 x-ray fluorescence studies of (+)-tartaric acid, carried out in the Netherlands by Johannes Martin Bijvoet, proved that Fischer's choice was correct.
It is important to recognize that the sign of a compound's specific rotation (an experimental number) does not correlate with its configuration (D or L). It is a simple matter to measure an optical rotation with a polarimeter. Determining an absolute configuration usually requires chemical interconversion with known compounds by stereospecific reaction paths.
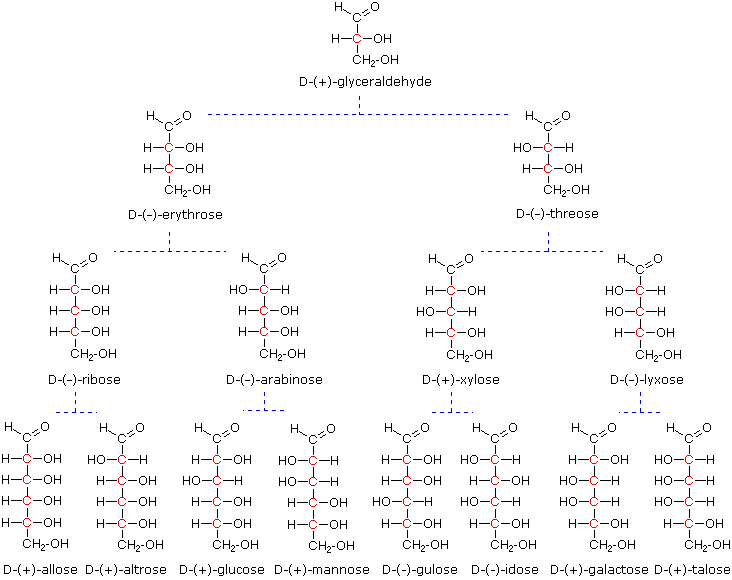
Exercise
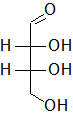
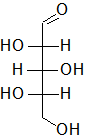
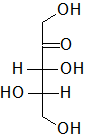
In the following Fischer projections, assign R and S for each chiral center and determine whether each sugar is a D or L sugar.
a)
b)
c)
- Answer
-
a) From top to bottom, 2R, 3R, and it is a D sugar.
b) From top to bottom, 2S, 3R, 4S, and it is an L sugar.
c) From to to bottom, 3R, 4S, and it is an L sugar.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry

