14.3: Kinetic vs. Thermodynamic Control of Reactions
- Page ID
- 67305
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- explain the difference between thermodynamic and kinetic control of a chemical reaction; for example, the reaction of a conjugated diene with one equivalent of hydrogen halide.
- draw a reaction energy diagram for a reaction which can result in both a thermodynamically controlled product and a kinetically controlled product.
- explain how reaction conditions can determine the product ratio in a reaction in which there is competition between thermodynamic and kinetic control.
Make certain that you can define, and use in context, the key terms below.
- kinetic control
- thermodynamic control
Like nonconjugated dienes, conjugated dienes are subject to attack by electrophiles. In fact, conjugated electrophiles experience relatively greater kinetic reactivity when reacted with electrophiles than nonconjugated dienes do. Upon electrophilic addition, the conjugated diene forms a mixture of two products—the kinetic product and the thermodynamic product—whose ratio is determined by the conditions of reaction. A reaction yielding more thermodynamic product is under thermodynamic control, and likewise, a reaction that yields more kinetic product is under kinetic control.
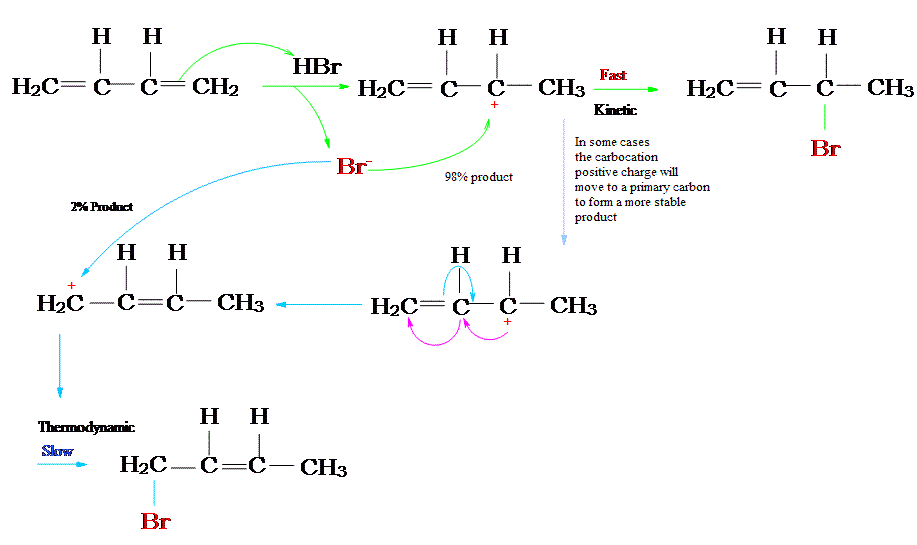
The reaction of one equivalent of hydrogen bromide with 1,3-butadiene gives different products at under different conditions and is a classic example of the concept of thermodynamic versus kinetic control of a reaction
Take a look at this energy profile diagram in Figure \(\PageIndex{1}\). In this scenario, the starting material \(\ce{A}\) can react to form either \(\ce{B}\) (to the left) or \(\ce{C}\) (to the right). The formation of the product \(\ce{B}\) involves overcoming barriers with lower activation energies, which means that it will form faster (ignoring the pre-exponential constant effects).
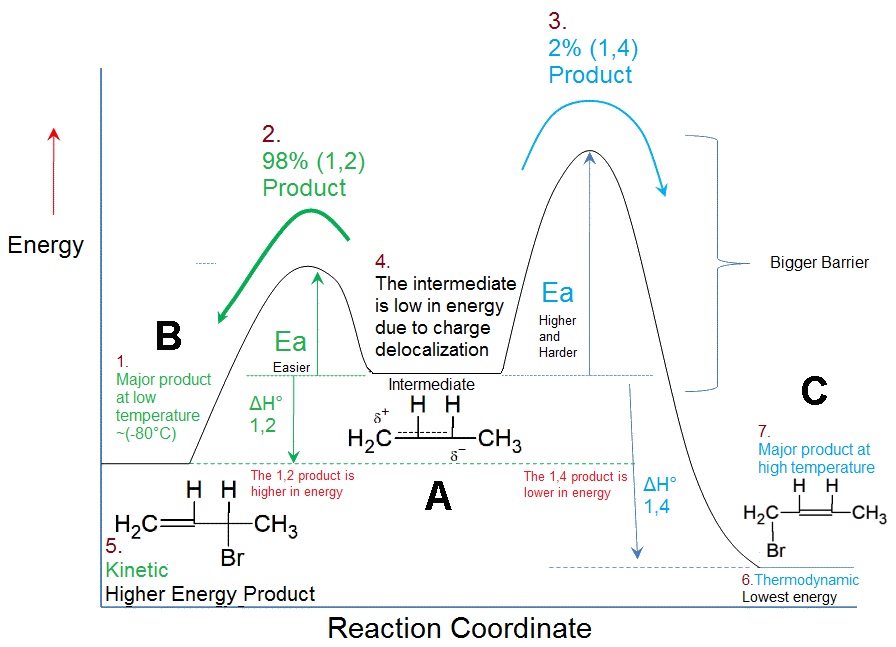
Figure \(\PageIndex{1}\): Energy profile diagram for A → B (left) and A → C (right). The horizontal axis is a reaction coordinate, and the vertical axis represents Gibbs energy. The delocalized carbocation intermediate (A) is the protonated form of 1,3-butadiene (first step of the reaction of 1,3-butadiene with HBr).
If we keep the temperature sufficiently low, the molecules of \(\ce{B}\), which are inevitably formed faster, will probably not have enough energy to overcome the reverse activation barrier (i.e., \(\ce{B} \rightarrow \ce{A}\)) to regenerate \(\ce{A}\) (Table \(\PageIndex{1}\)). The forward reactions \(\ce{A->B}\) and \(\ce{A->C}\) are, under such conditions, effectively irreversible. Since the formation of \(\ce{B}\) is faster, it will predominate, and the major product formed will be \(\ce{B}\). This is known as kinetic control and \(\ce{B}\) is the kinetic product.
At elevated temperatures, \(\ce{B}\) is still going to be the product that is formed faster. However, it also means that all the reactions will be reversible. This means that molecules of \(\ce{B}\) can revert back to \(\ce{A}\). Since the system is no longer limited by temperature, the system will minimize its Gibbs free energy, which is the thermodynamic criterion for chemical equilibrium. This means that, as the most thermodynamically stable molecule, \(\ce{C}\) will be predominantly formed.2 The reaction is said to be under thermodynamic control and \(\ce{C}\) is the thermodynamic product.
| Temperature | Kinetic or Thermodynamically Controlled | Speed of Reaction | 1,2-adduct (B) : 1,4-adduct (C) Ratio |
|---|---|---|---|
| -15 °C | Kinetic | Fast | 70:30 |
| 0 °C | Kinetic | Fast | 60:40 |
| 40 °C | Thermodynamic | Slow | 15:85 |
| 60 °C | Thermodynamic | Slow | 10:90 |
A simple definition is that the kinetic product is the product that is formed faster, and the thermodynamic product is the product that is more stable. This is precisely what is happening here. The kinetic product is 3-bromobut-1-ene, and the thermodynamic product is 1-bromobut-2-ene (specifically, the trans isomer).
Note that not every reaction has an energy profile diagram like Figure \(\PageIndex{1}\), and not every reaction has different thermodynamic and kinetic products! If the transition states leading to the formation of B were to be higher in energy than that leading to C, then C would simultaneously be both the thermodynamic and kinetic product. There are plenty of reactions in which the more stable product (thermodynamic) is also formed faster (kinetic).
The Reaction Mechanism
The first step is the protonation of one of the \(\ce{C=C}\) double bonds. In butadiene (1), both double bonds are the same, so it does not matter which one is protonated. The protonation occurs regioselectively to give the more stable carbocation (i.e., IB=IC in Figure \(\PageIndex{1}\)1):
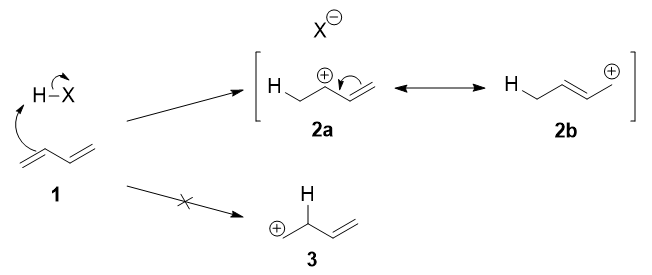
The more stable cation is not only secondary, but also allylic, and therefore enjoys stabilization via resonance (or conjugation). This is depicted in the resonance forms 2a and 2b above. This allylic carbocation, more properly denoted as the resonance hybrid 2, has two carbons which have significant positive charge, and the bromide ion (here denoted as \(\ce{X-}\)) can attack either carbon. Attacking the central carbon, adjacent to the site of protonation, leads to the kinetic product 3 (called the 1,2-adduct); attacking the terminal carbon, distant from the site of protonation, leads to the thermodynamic product 4 (called the 1,4-adduct).
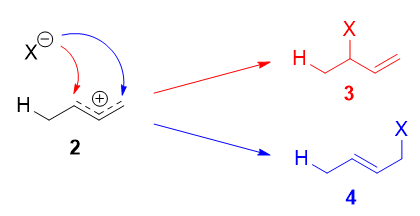
There are some people who write that 3 results from attack of \(\ce{X-}\) on resonance form 2a, and 4 from attack of \(\ce{X-}\) on resonance form 2b. This is not correct! Resonance forms do not separately exist, and they are not distinct species that rapidly interconvert. As such, one cannot speak of one single resonance form undergoing a reaction.
Now, why 4 is the thermodynamic product, and why 3 is the kinetic product for this reaction?
The thermodynamic product: trans-1-bromobut-2-ene
It is perhaps simple enough to see why 4 is more stable than 3. It has an internal, disubstituted double bond, and we know that as a general rule of thumb, the thermodynamic stability of an alkene increases with increasing substitution. So, compared to the terminal, monosubstituted alkene 3, 4 is more stable.
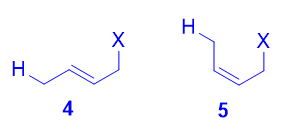
Both the trans isomer 4 as well as the cis isomer 5 can be formed via attack of the nucleophile at the terminal carbon, and both are disubstituted alkenes. However, the trans isomer 4 is more stable than the cis isomer 5, because there is less steric repulsion between the two substituents on the double bond. As such, 4 is the thermodynamic product.
The kinetic product: 3-bromobut-1-ene
Several explanations may be proposed to explain the nature of the kinetic product.
The worst possible argument argues that the resonance form 2a, being an allylic secondary carbocation, is more stable than resonance form 2b, which is an allylic primary carbocation. Therefore, resonance form 2a exists in greater relative proportion (i.e., more molecules will look like 2a than 2b), and the nucleophile preferentially reacts with this specific carbocation, leading to the formation of 3. However, this is incorrect, since individual resonance forms do not exist. Moreover, such an argument suggests that we are looking for the more stable intermediate (IB or IC in Figure \(\PageIndex{1}\)). In fact, we should be looking for the more stable transition states (TB1, TB2, TC1, and TC2 in Figure \(\PageIndex{1}\)). The carbocation is an intermediate, and not a transition state.
The most common argument is since resonance form 2a is more stable than 2b, is that it contributes more towards the resonance hybrid 2. As such, the positive charge on the internal carbon is greater than the positive charge on the terminal carbon. The nucleophile, being negatively charged, is more strongly attracted to the more positively charged or more electrophilic carbon, and therefore attack there occurs faster (the transition state being stabilized by greater electrostatic interactions). That's actually a very sensible explanation; with only the data that has been presented so far, we would not be able to disprove it, and it was indeed the accepted answer for quite a while.
Experimental Results
In 1979, Nordlander et al. carried out a similar investigation on the addition of \(\ce{DCl}\) to a different substrate, 1,3-pentadiene.7 This experiment was ingenious, because it was designed to proceed via an almost symmetrical intermediate:

Resonance forms 7a and 7b are both allylic and secondary. There is a very minor difference in their stabilities arising from the different hyperconjugative ability of \(\ce{C-D}\) vs \(\ce{C-H}\) bonds, but in any case, it is not very large. Therefore, if we adopt the explanation in the previous section, one would expect there not to be any major kinetic pathway, and both 1,2- and 1,4-addition products (8 and 9) would theoretically be formed roughly equally.
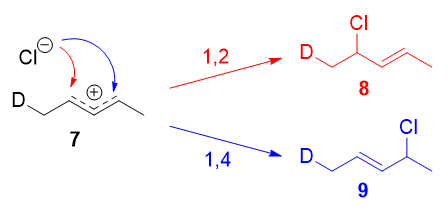
Instead, it was found that the 1,2-addition product was favored over the 1,4-addition product. For example, at \(-78\ ^\circ\mathrm{C}\) in the absence of solvent, there was a roughly \(75:25\) ratio of 1,2- to 1,4-addition products. Clearly, there is a factor that favors 1,2-addition that does not depend on the electrophilicity of the carbon being attacked! The authors attributed this effect to an ion pair mechanism. This means that, after the double bond is protonated (deuterated in this case), the chloride counterion remains in close proximity to the carbocation generated. Immediately following dissociation of \(\ce{DCl}\), the chloride ion is going to be much closer to \(\ce{C-2}\) than it is to \(\ce{C-4}\), and therefore attack at \(\ce{C-2}\) is much faster. In fact, normal electrophilic addition of \(\ce{HX}\) to conjugated alkenes in polar solvents can also proceed via similar ion pair mechanisms. This is reflected by the greater proportion of syn addition products to such substrates.11
The mechanism that favors 1,2-addition clearly does not depend on the electrophilicity of the carbon being attacked.
This ion pair mechanism is a pre-exponential constant effects that is attributed to the proximity and frequency of collision rather than a activation barrier effect.
Conclusion
The reactivity of conjugated dienes (hydrocarbons that contain two double bonds) varies depending on the location of double bonds and temperature of the reaction.These reactions can produce both thermodynamic and kinetic products. Isolated double bonds provide dienes with less stability thermodynamically than conjugated dienes. However, they are more reactive kinetically in the presence of electrophiles and other reagents. This is a result of Markovnikov addition to one of the double bonds. A carbocation is formed after a double bond is opened. This carbocation has two resonance structures and addition can occur at either of the positive carbons.
References
- Smith, M. B. March's Advanced Organic Chemistry, 7th ed., p 272
- This does not mean that all of \(\ce{A}\) will be converted to \(\ce{B}\); the reaction is still an equilibrium, and equilibria always go forward and backward. In general, the minimum system Gibbs free energy (\(G_\mathrm{syst}\)) will occur at a certain proportion of \(\ce{A}\), \(\ce{B}\), and \(\ce{C}\). However, since \(\ce{B}\) has the lowest Gibbs free energy, it will be formed in a greater proportion than \(\ce{C}\).
- http://www.ochempal.org/index.php/alphabetical/a-b/14-addition/
- J. Am. Chem. Soc. 1979, 101 (5), 1288–1289
- Because of the larger reduced mass and lower zero-point energy, a $\ce{C-D}$ bond is stronger and therefore less willing to donate electron density into an adjacent empty $\mathrm{p}$ orbital. This is the origin of some secondary kinetic isotope effects; in our case, it means that 7a is marginally less stable than 7b.
- J. Am. Chem. Soc. 1969, 91 (14), 3865–3869
- Addition of \(\ce{HX}\) to butadiene in the gas phase gives approximately a \(1:1\) ratio of 1,2- to 1,4-addition product, suggesting that an ion pair mechanism (which would favor the 1,2-addition product) does not operate: J. Org. Chem., 1991, 56 (2), 595–601
Practice Problems
- Write out the products of 1,2 addition and 1,4- addition of a) HBr and b) DBr to 1,3-cyclo-hexadiene. What is unusual about the products of 1,2- and 1,4- addition of HX to unsubstituted cyclic 1,3-dienes?
- Is the 1,2-addition product formed more rapidly at higher temperatures, even though it is the 1,4-addition product that predominates under these conditions?
- Why is the 1,4-addition product the thermodynamically more stable product?
- Out of the following radical cations which one is not a reasonable resonance structure?

5. Addition of 1 equivalent of Bromine to 2,4-hexadiene at 0 degrees C gives 4,5-dibromo-2-hexene plus an isomer. Which of the following is that isomer:
- 5,5-dibromo-2-hexene
- 2,5-dibromo-3-hexene
- 2,2-dibromo-3-hexene
- 2,3-dibromo-4-hexene
6. Which of the following will be the kinetically favored product from the depicted reaction?
7. Addition of HBr to 2,3-dimethyl-1,3-cyclohexadiene may occur in the absence or presence of peroxides. In each case two isomeric C8H13Br products are obtained. Which of the following is a common product from both reactions?
8. and 9.
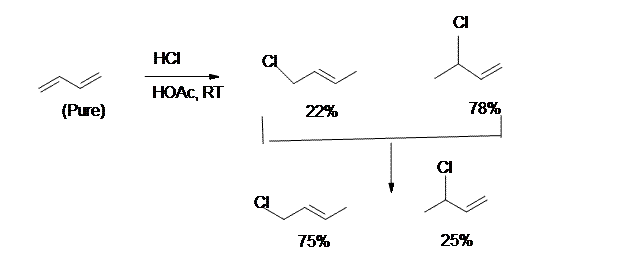
8. The kinetically controlled product in the above reaction is:
- 3-Chloro-1-Butene
- 1-Chloro-2-Butene
9. For the reaction in question 8, which one is the result of 1,4-addition?
- 3-Chloro-1-Butene
- 1-Chloro-2-Butene
Answers to Problems
1. A) Same product for both modes of addition.

B) Both cis and trans isomers will form.
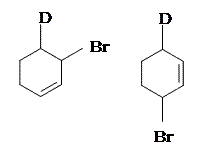
Addition of the HX to unsubstituted cycloalka-1,3-dienes in either 1,2- or 1,4- manner gives the same product becasuse of symmetry.
2. Yes. the Kinetic Product will still form faster but in this case there will be enough energy to form the thermodynamic product because the thermodynamic product is still more stable.
3. The 1,4- product is more thermodynamically stable because there are two alkyl groups on each side of the double bond. This form offers stability to the overall structure.
4. All of these isomers are viable.
5. B
6. C
7. D
8. A
9. B
Exercise
1) Why is the 1,4-addition product the thermodynamically more stable product?
2) Addition of 1 equivalent of bromine to 2,4-hexadiene at 0 degrees C gives 4,5-dibromo-2-hexene plus an isomer. What is the structure of that isomer?
3) The kinetically controlled product in the below reaction is:

4) For the reaction above, which product is the result of 1,4-addition?

5) What would be the major product of the addition of HBr to 2,3-dimethyl-1,3-cyclohexadiene under thermodynamic conditions?
6) Consider the reaction with 1,3-buta-diene reacting with HCl. Propose a mechanism for the reaction. Also, Predict why the 1,4 adduct is the major product in this reaction compared to the 1,2.
- Answer
-
1) The 1,4- product is more thermodynamically stable because there are two alkyl groups on each side of the double bond and more substituted alkenes are more stable.
2) 2,5-Dibromo-3-hexene
3) 3-Chloro-1-butene
4) 1-Chloro-2-butene
5)

6)
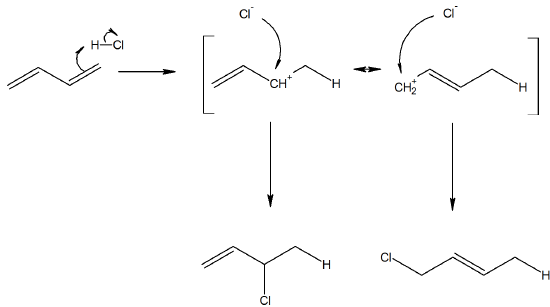
Even though the cation would prefer to be in a secondary position in the transition state, the final product is less stable with a terminal alkene. Therefore the major product will be the 1,4 adduct.
Contributors and Attributions
- Orthocresol (@chemistry StackExchange)
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
- Natasha Singh

