14.2: Electrophilic Additions to Conjugated Dienes- Allylic Carbocations
- Page ID
- 67304
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- write an equation for the addition of one or two mole equivalents of a halogen or a hydrogen halide to a nonconjugated diene.
- write an equation for the addition of one or two mole equivalents of a halogen or a hydrogen halide to a conjugated diene.
- write the mechanism for the addition of one mole equivalent of hydrogen halide to a conjugated diene, and hence account for the formation of 1,2- and 1,4-addition products.
- explain the stability of allylic carbocations in terms of resonance.
- draw the resonance contributors for a given allylic carbocation.
- predict the products formed from the reaction of a given conjugated diene with one mole equivalent of halogen or hydrogen halide.
- predict which of the possible 1,2- and 1,4-addition products is likely to predominate when one mole equivalent of a hydrogen halide is reacted with a given conjugated diene.
- use the concept of carbocation stability to explain the ratio of the products obtained when a given conjugated diene is reacted with one mole equivalent of hydrogen halide.
Make certain that you can define, and use in context, the key terms below.
- 1,2-addition
- 1,4-addition
Notice that the numbers used in the expressions 1,2-addition and 1,4-addition do not refer to the positions of the carbon atoms in the diene molecule. Here, 1,2 indicates two neighbouring carbon atoms, while 1,4 indicates two carbon atoms which are separated in the carbon chain by two additional carbon atoms. Thus in 1,2- and 1,4-additions to 2,4-hexadiene, the additions actually occur at carbons 2 and 3, and 2 and 5, respectively.
The term “monoadduct” should be interpreted as meaning the product or products formed when one mole of reagent adds to one mole of substrate. In the objectives above, this process is referred to as the addition of one mole equivalent (or one mol equiv).
In Section 7.9 we saw that electrophilic addition to a simple alkene would follow Markovnikov’s rule, where the stability of the carbocation intermediate would increase: primary < secondary < tertiary. With conjugated dienes the allylic carbocation intermediately generated has different resonance forms. The following scheme represents the mechanism for the addition of HBr to 1,3-butadiene (at 0°C). Note the resonance contributors for the allylic carbocation intermediate and that the product resulting from the secondary cation is generated in higher yield than from the primary cation as you might expect from our discussions until now. However, in the next section you will see that the resulting product ratio can be drastically affected by a number of reaction conditions, including temperature.
The reactions of 1,3-butadiene are reasonably typical of conjugated dienes. The compound undergoes the usual reactions of alkenes, such as catalytic hydrogenation or radical and polar additions, but it does so more readily than most alkenes or dienes that have isolated double bonds. Furthermore, the products frequently are those of 1,2 and 1,4 addition:


Formation of both 1,2- and 1,4-addition products occurs not only with halogens, but also with other electrophiles such as the hydrogen halides. The mechanistic course of the reaction of 1,3-butadiene with hydrogen chloride is shown in Equation 13-1. The first step, as with alkenes, is formation of a carbocation. However, with 1,3-butadiene, if the proton is added to \(\ce{C_1}\) (but not \(\ce{C_2}\)), the resulting cation has a substantial delocalization energy, with the charge distributed over two carbons (review Sections 6-5 and 6-5C if this is not clear to you). Attack of \(\ce{Cl}^\ominus\) as a nucleophile at one or the other of the positive carbons yields the 1,2- or the 1,4- addition product:

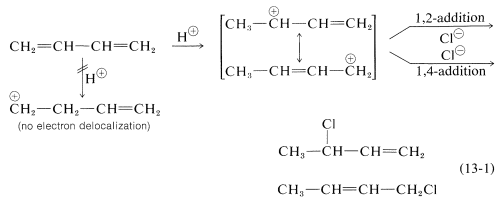
An important feature of reactions in which 1,2 and 1,4 additions occur in competition with one another is that the ratio of the products can depend on the temperature, the solvent, and also on the total time of reaction.
Exercise
- Give the 1,2 and the 1,4 products of the addition of one equivalent of HBr to 1,3-hexa-diene.
- Look at the previous addition reaction of HBr with a diene. Consider the transition states, predict which of them would be the major products and which will be the minor.
- Write out the products of 1,2 addition and 1,4- addition of HBr to 1,3-cyclohexadiene.
- What is unusual about the products of 1,2- and 1,4- addition of HX to an unsubstituted cyclic 1,3-diene?
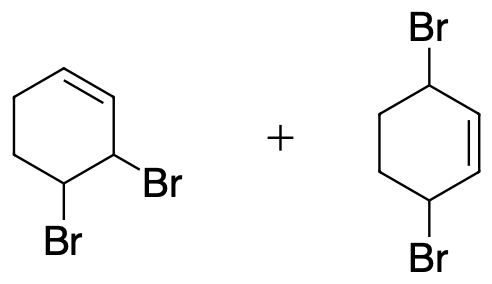
- Write out the products of 1,2 addition and 1,4- addition of Br2 to 1,3-cyclohexadiene.
- Answer
-
1)

2) The products i-iii all show a secondary cation intermediate which is more stable than primary. Therefore those would be major products and the iv product would be the minor product.
.png?revision=1&size=bestfit&width=731&height=380)
3) The same product will result from 1,2 and 1,4 addition.
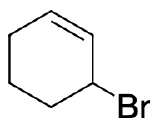
4) Addition of the HX to unsubstituted cycloalka-1,3-dienes in either 1,2- or 1,4- manner gives the same product because of symmetry.
5) Both 1,2 and 1,4 products will form.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
John D. Robert and Marjorie C. Caserio (1977) Basic Principles of Organic Chemistry, second edition. W. A. Benjamin, Inc. , Menlo Park, CA. ISBN 0-8053-8329-8. This content is copyrighted under the following conditions, "You are granted permission for individual, educational, research and non-commercial reproduction, distribution, display and performance of this work in any format."

