14.1: Stability of Conjugated Dienes- Molecular Orbital Theory
- Page ID
- 67303
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- write a reaction sequence to show a convenient method for preparing a given conjugated diene from an alkene, allyl halide, alkyl dihalide or alcohol (diol).
- identify the reagents needed to prepare a given diene from one of the starting materials listed in Objective 1, above.
- compare the stabilities of conjugated and nonconjugated dienes, using evidence obtained from hydrogenation experiments.
- discuss the bonding in a conjugated diene, such as 1,3-butadiene, in terms of the hybridization of the carbon atoms involved.
- discuss the bonding in 1,3-butadiene in terms of the molecular orbital theory, and draw a molecular orbital for this and similar compounds.
Make certain that you can define, and use in context, the key terms below.
- delocalized electrons
- node
The two most frequent ways to synthesize conjugated dienes are dehydration of alcohols and dehydrohalogenation of organohalides, which were introduced in the preparation of alkenes (Section 8.1). The following scheme illustrates some of the routes to preparing a conjugated diene.
The formation of synthetic polymers from dienes such as 1,3-butadiene and isoprene is discussed in Section 14.6. Synthetic polymers are large molecules made up of smaller repeating units. You are probably somewhat familiar with a number of these polymers; for example, polyethylene, polypropylene, polystyrene and poly(vinyl chloride).
As the hydrogenation of 1,3-butadiene releases less than the predicted amount of energy, the energy content of 1,3-butadiene must be lower than we might have expected. In other words, 1,3-butadiene is more stable than its formula suggests.
Figure 14.1: Energy diagram for the hydrogenation of 1,3-butadiene (not to scale).
Some university-level general chemistry courses do not introduce the subject of molecular orbitals. If you have taken such a course, or forgotten what is meant by the term “molecular orbital,” combine a review of Section 1.11 with your study of this section.
Conjugated dienes are more stable than non conjugated dienes (both isolated and cumulated) due to factors such as delocalization of charge through resonance and hybridization energy. This can also explain why allylic radicals are much more stable than secondary or even tertiary carbocations. This is all due to the positioning of the pi orbitals and ability for overlap to occur to strengthen the single bond between the two double bonds.
The resonance structure shown below gives a good understanding of how the charge is delocalized across the four carbons in this conjugated diene. This delocalization of charges stablizes the conjugated diene:

Along with resonance, hybridization energy effect the stability of the compound. For example in 1,3-butadiene the carbons with the single bond are sp2 hybridized unlike in nonconjugated dienes where the carbons with single bonds are sp3 hybridized. This difference in hybridization shows that the conjugated dienes have more 's' character and draw in more of the pi electrons, thus making the single bond stronger and shorter than an ordinary alkane C-C bond (1.54Å).

Another useful resource to consider are the heats of hydrogenation of different arrangements of double bonds. Since the higher the heat of hydrogenation the less stable the compound, it is shown below that conjugated dienes (~54 kcal) have a lower heat of hydrogenation than their isolated (~60 kcal) and cumulated diene (~70 kcal) counterparts.
Here is an energy diagram comparing different types of bonds with their heats of hydrogenation to show relative stability of each molecule:
The stabilization of dienes by conjugation is less dramatic than the aromatic stabilization of benzene. Nevertheless, similar resonance and molecular orbital descriptions of conjugation may be written.
Allylic Carbocation
Conjugation occurs when p orbital on three or more adjacent atoms can overlap Conjugation tends to stabilize molecules
Allylic carbocations are a common conjugated system.
The positive charge of a carbocation is contained in a P orbital of a sp2 hybrizied carbon. This allows for overlap with double bonds. The positive charge is more stable because it is spread over 2 carbons.

Molecular Orbitals of an Allylic Carbocation
The stability of the carbocation of propene is due to a conjugated π electron system. A "double bond" doesn't really exist. Instead, it is a group of 3 adjacent, overlapping, non-hybridized p orbitals we call a conjugated π electron system. You can clearly see the interactions between all three of the p orbitals from the three carbons resulting in a really stable cation. It all comes down to where the location of the electron-deficient carbon is.
Molecular orbital descriptions can explain allylic stability in yet another way using 2-propenyl. Fig.6
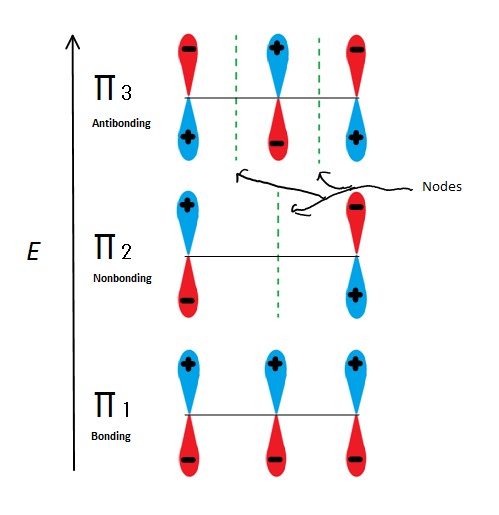
Fig.6 Shows the 3 possible Molecular orbitals of 2-propenyl
If we just take the π molecular orbital and not any of the s, we get three of them. π1 is bonding with no nodes, π2 is nonbonding (In other words, the same energy as a regular p-orbital) with a node, and π3 is antibonding with 2 nodes (none of the orbitals are interacting). The first two electrons will go into the π1 molecular orbital, regardless of whether it is a cation, radical, or anion. If it is a radical or anion, the next electron goes into the π2 molecular orbital. The last anion electron goes into the nonbonding orbital also. So no matter what kind of carbon center exists, no electron will ever go into the antibonding orbital.
The Bonding orbitals are the lowest energy orbitals and are favorable, which is why they are filled first. Even though the nonbonding orbitals can be filled, the overall energy of the system is still lower and more stable due to the filled bonding molecular orbitals.
This figure also shows that π2 is the only molecular orbital where the electrion differs, and it is also where a single node passes through the middle. Because of this, the charges of the molecule are mainly on the two terminal carbons and not the middle carbon.
This molecular orbital description can also illustrate the stability of allylic carbon centers in figure 7.
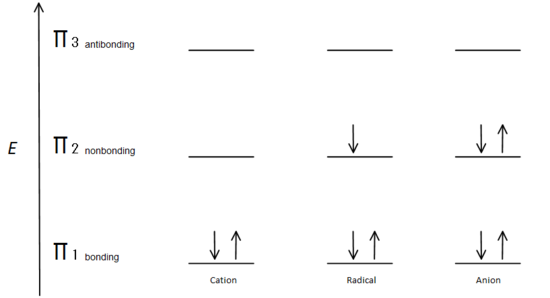
Fig. 7: diagram showing how the electrons fill based on the Aufbau principle.
The π bonding orbital is lower in energy than the nonbonding p orbital. Since every carbon center shown has two electrons in the lower energy, bonding π orbitals, the energy of each system is lowered overall (and thus more stable), regardless of cation, radical, or anion.
1,3-Dienes
Conjugated double bonds are separated by a single bond. 1,3-dienes are an excellent example of a conjugated system. Each carbon in 1,3 dienes are sp2 hybridized and therefore have one p orbital. The four p orbitals in 1,3-butadiene overlap to form a conjugated system.
Conjugated vs. Nonconjugated Dienes
Conjugated dienes are two double bonds separated by a single bond
.bmp?revision=1&size=bestfit&width=182&height=64)
Nonconjugated (Isolated) Dienes are two double bonds are separated by more than one single bond.
.bmp?revision=1&size=bestfit&width=159&height=64)
When using electrostatic potential maps, it is observed that the pi electron density overlap is closer together and delocalized in conjugated dienes, while in non conjugated dienes the pi electron density is located differently across the molecule. Since having more electron density delocalized makes the molecule more stable conjugated dienes are more stable than non conjugated
For example in 1,3-butadiene the carbons with the single bond are sp2 hybridized unlike in nonconjugated dienes where the carbons with single bonds are sp3 hybridized. This difference in hybridization shows that the conjugated dienes have more 's' character and draw in more of the pi electrons, thus making the single bond stronger and shorter than an ordinary alkane C-C bond (1.54Å).
Stability of Conjugated Dienes
Conjugated dienes are more stable than non conjugated dienes (both isolated and cumulated) due to factors such as delocalization of charge through resonance and hybridization energy. This can also explain why allylic radicals are much more stable than secondary or even tertiary carbocations. This is all due to the positioning of the pi orbitals and ability for overlap to occur to strengthen the single bond between the two double bonds.
The resonance structure shown below gives a good understanding of how the charge is delocalized across the four carbons in this conjugated diene. This delocalization of charges stabilizes the conjugated diene:

Along with resonance, hybridization energy effect the stability of the compound. For example in 1,3-butadiene the carbons with the single bond are sp2 hybridized unlike in nonconjugated dienes where the carbons with single bonds are sp3 hybridized. This difference in hybridization shows that the conjugated dienes have more 's' character and draw in more of the pi electrons, thus making the single bond stronger and shorter than an ordinary alkane C-C bond (1.54Å).
Molecular Orbitals of 1,3 Dienes
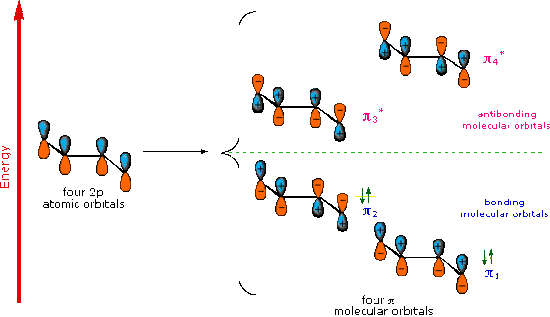
A molecular orbital model for 1,3-butadiene is shown below. Note that the lobes of the four p-orbital components in each pi-orbital are colored differently and carry a plus or minus sign. This distinction refers to different phases, defined by the mathematical wave equations for such orbitals. Regions in which adjacent orbital lobes undergo a phase change are called nodes. Orbital electron density is zero in such regions. Thus a single p-orbital has a node at the nucleus, and all the pi-orbitals shown here have a nodal plane that is defined by the atoms of the diene. This is the only nodal surface in the lowest energy pi-orbital, π1. Higher energy pi-orbitals have an increasing number of nodes.
Exercise
The heat of hydrogenation for allene is about 300 kJ/mol. Order a conjugated diene, a non-conjugated diene, and allene in increasing stability.
- Answer
-
allene < non-conjugated diene < conjugated diene (most stable)
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
William Reusch, Professor Emeritus (Michigan State U.), Virtual Textbook of Organic Chemistry
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

