13.12: More Complex Spin-Spin Splitting Patterns
- Page ID
- 67298
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- explain how multiple coupling can give rise to complex-looking 1H NMR spectra.
- predict the splitting pattern expected in the 1H NMR spectrum of an organic compound in which multiple coupling is possible.
- interpret 1H NMR spectra in which multiple coupling is evident.
Make certain that you can define, and use in context, the key term below.
- tree diagram
We saw the effects of spin-spin coupling on the appearance of a 1H NMR signal. These effects can be further complicated when that signal is coupled to several different protons. For example, BrCH2CH2CH2Cl would produce three signals. The hydrogens at C1 and C3 would each be triplets because of coupling to the two hydrogens on C2. However, the hydrogen on C2 “sees” two different sets of neighbouring hydrogens, and would therefore produce a triplet of triplets.
Another effect that can complicate a spectrum is the “closeness” of signals. If signals accidently overlap they can be difficult to identify. In the example above, we expected a triplet of triplets. However, if the coupling is identical (or almost identical) between the hydrogens on C2 and the hydrogens on both C1 and C3, one would observe a quintet in the 1H NMR spectrum. [You can try this yourself by drawing a tree diagram of a triplet of triplets assuming, first, different coupling constants, and then, identical coupling constants.] Keep this point in mind when interpreting real 1H NMR spectra.
Also, when multiplets are well separated, they form patterns. However, when multiplets approach each other in the spectrum they sometimes become distorted. Usually, the inner peaks become larger than the outer peaks. Note the following examples:
Aromatic ring protons quite commonly have overlapping signals and multiplet distortions. Sometimes you cannot distinguish between individual signals, and one or more messy multiplets often appear in the aromatic region.
It is much easier to rationalize the observed 1H NMR spectrum of a known compound than it is to determine the structure of an unknown compound from its 1H NMR spectrum. However, rationalizations can be a useful learning technique as you try to improve your proficiency in spectral interpretation. Remember that when a chemist tries to interpret the 1H NMR spectrum of an unknown compound, he or she usually has additional information available to make the task easier. For example, the chemist will almost certainly have an infrared spectrum of the compound and possibly a mass spectrum too. Details of how the compound was synthesized may be available, together with some indication of its chemical properties, its physical properties, or both.
In examinations, you will be given a range of information (IR, MS, UV data and empirical formulae) to aid you with your structural determination using 1H NMR spectroscopy. For example, you may be asked to determine the structure of C6H12O given the following spectra:
Infrared spectrum: 3000 cm−1 and 1720 cm−1 absorptions are both strong
| 1H NMR | δ (ppm) | Protons | Multiplicity |
|---|---|---|---|
| 0.87 | 6 | doublet | |
| 1.72 | 1 | broad multiplet | |
| 2.00 | 3 | singlet | |
| 2.18 | 2 | doublet |
To answer this question, you note that the infrared spectrum of C6H12O shows $\ce{\sf{C-H}}$ stretching (3000 cm−1) and $\ce{\sf{C-O}}$ stretching (1720 cm−1). Now you have to piece together the information from the 1H NMR spectrum. Notice the singlet with three protons at 2.00 ppm. This signal indicates a methyl group that is not coupled to other protons. It could possibly mean the presence of a methyl ketone functional group.
The signal at 1.72 ppm is a broad multiplet, suggesting that a carbon with a single proton is beside carbons with several different protons.
The doublet signal at 2.18 ppm implies that a $\ce{\sf{-CH2-}}$ group is attached to a carbon having only one proton.
The six protons showing a doublet at 0.87 ppm indicate two equivalent methyl groups attached to a carbon with one proton.
Whenever you see a signal in the 0.7-1.3 ppm range that is a multiplet of three protons (3, 6, 9) it is most likely caused by equivalent methyl groups.
Using trial and error, and with the above observations, you should come up with the correct structure.
Complex coupling
In all of the examples of spin-spin coupling that we have seen so far, the observed splitting has resulted from the coupling of one set of hydrogens to just one neighboring set of hydrogens. When a set of hydrogens is coupled to two or more sets of nonequivalent neighbors, the result is a phenomenon called complex coupling. A good illustration is provided by the 1H-NMR spectrum of methyl acrylate:
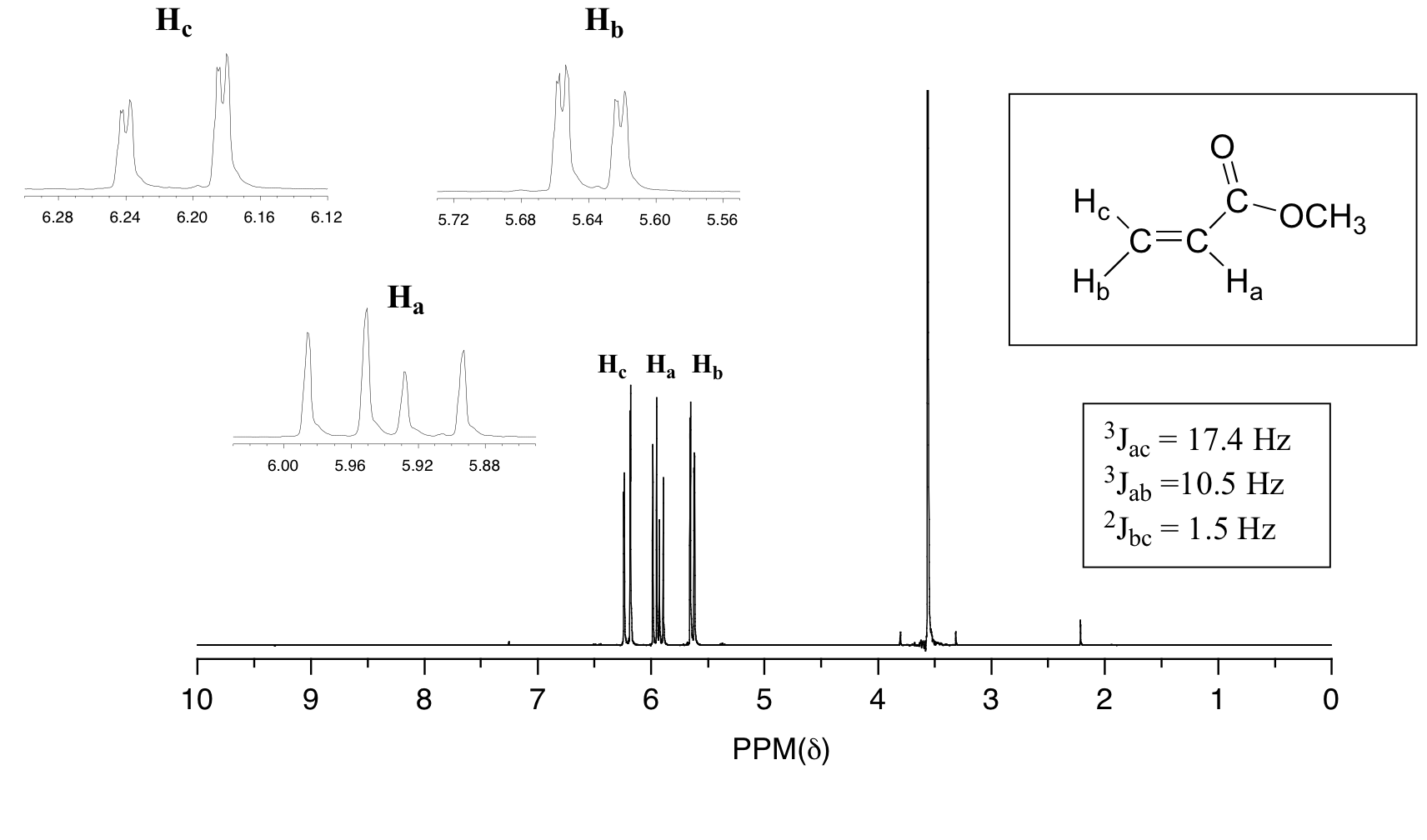 First, let's first consider the Hc signal, which is centered at 6.21 ppm. Here is a closer look:
First, let's first consider the Hc signal, which is centered at 6.21 ppm. Here is a closer look:
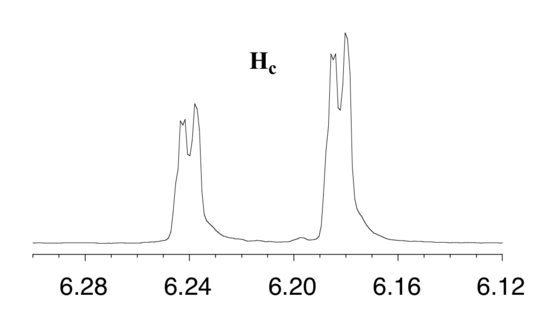
With this enlargement, it becomes evident that the Hc signal is actually composed of four sub-peaks. Why is this? Hc is coupled to both Ha and Hb , but with two different coupling constants. Once again, a splitting diagram (or tree diagram) can help us to understand what we are seeing. Ha is trans to Hc across the double bond, and splits the Hc signal into a doublet with a coupling constant of 3Jac = 17.4 Hz. In addition, each of these Hc doublet sub-peaks is split again by Hb (geminal coupling) into two more doublets, each with a much smaller coupling constant of 2Jbc = 1.5 Hz.
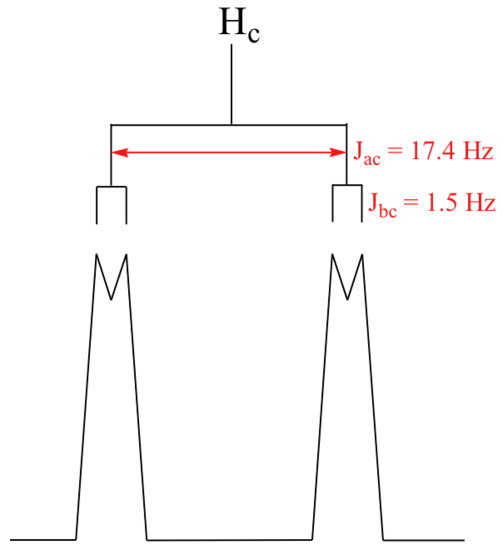
The result of this `double splitting` is a pattern referred to as a doublet of doublets, abbreviated `dd`.
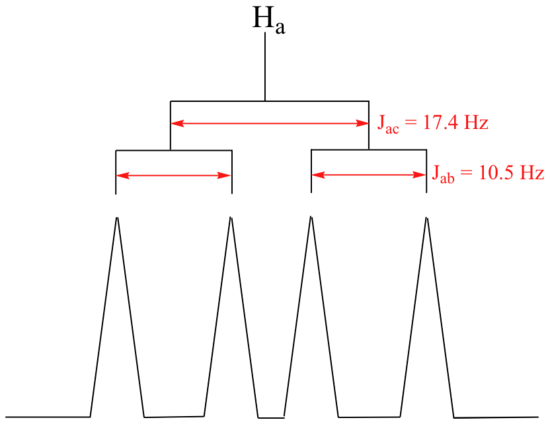
The signal for Ha at 5.95 ppm is also a doublet of doublets, with coupling constants 3Jac= 17.4 Hz and 3Jab = 10.5 Hz.
The signal for Hb at 5.64 ppm is split into a doublet by Ha, a cis coupling with 3Jab = 10.4 Hz. Each of the resulting sub-peaks is split again by Hc, with the same geminal coupling constant 2Jbc = 1.5 Hz that we saw previously when we looked at the Hc signal. The overall result is again a doublet of doublets, this time with the two `sub-doublets` spaced slightly closer due to the smaller coupling constant for the cis interaction. Here is a blow-up of the actual Hbsignal:
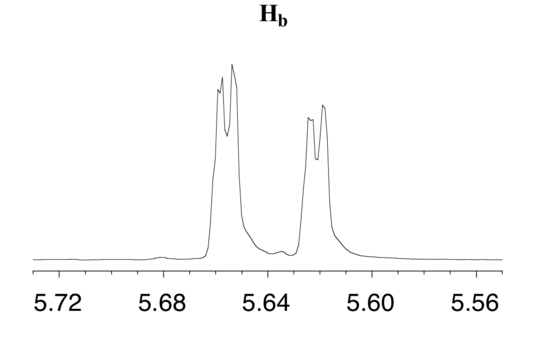
Construct a splitting diagram for the Hb signal in the 1H-NMR spectrum of methyl acrylate. Show the chemical shift value for each sub-peak, expressed in Hz (assume that the resonance frequency of TMS is exactly 300 MHz).
Solution:
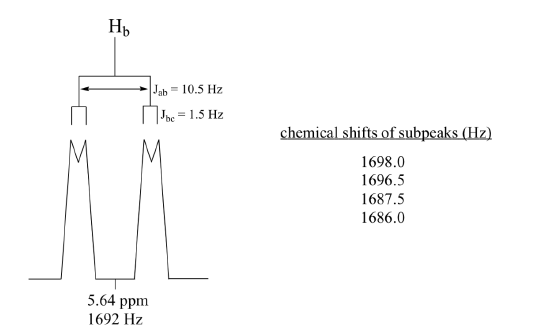
When constructing a splitting diagram to analyze complex coupling patterns, it is usually easier to show the larger splitting first, followed by the finer splitting (although the reverse would give the same end result).
When a proton is coupled to two different neighboring proton sets with identical or very close coupling constants, the splitting pattern that emerges often appears to follow the
When a proton is coupled to two different neighboring proton sets with identical or very close coupling constants, the splitting pattern that emerges often appears to follow the simple `n + 1 rule` of non-complex splitting. In the spectrum of 1,1,3-trichloropropane, for example, we would expect the signal for Hb to be split into a triplet by Ha, and again into doublets by Hc, resulting in a 'triplet of doublets'.
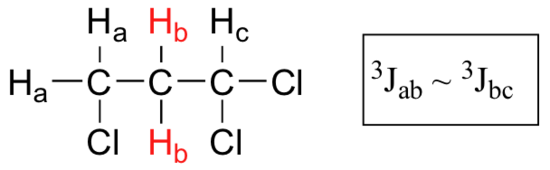
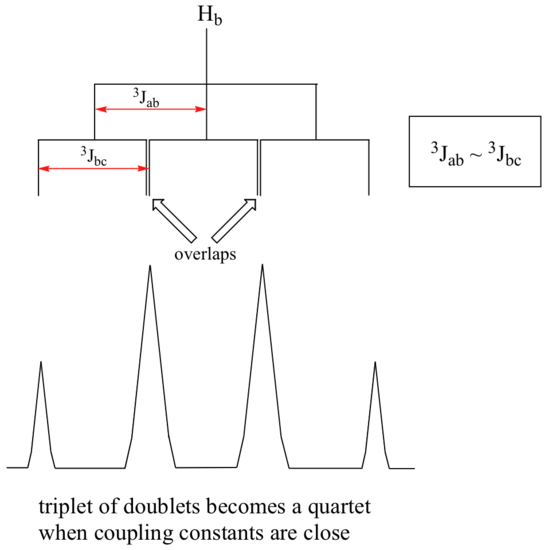
Ha and Hc are not equivalent (their chemical shifts are different), but it turns out that 3Jab is very close to 3Jbc. If we perform a splitting diagram analysis for Hb, we see that, due to the overlap of sub-peaks, the signal appears to be a quartet, and for all intents and purposes follows the n + 1 rule.
For similar reasons, the Hc peak in the spectrum of 2-pentanone appears as a sextet, split by the five combined Hb and Hd protons. Technically, this 'sextet' could be considered to be a 'triplet of quartets' with overlapping sub-peaks.

What splitting pattern would you expect for the signal coresponding to Hb in the molecule below? Assume that Jab ~ Jbc. Draw a splitting diagram for this signal, and determine the relative integration values of each subpeak.
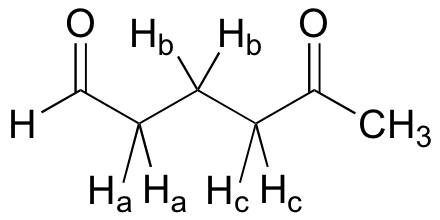
Solution: We can think of this signal as being a triplet of triplets, but because the two coupling constants are very close, what we would actually see is a 1,2,3,2,1 pentet.
In many cases, it is difficult to fully analyze a complex splitting pattern. In the spectrum of toluene, for example, if we consider only 3-bond coupling we would expect the signal for Hb to be a doublet, Hd a triplet, and Hc a triplet.
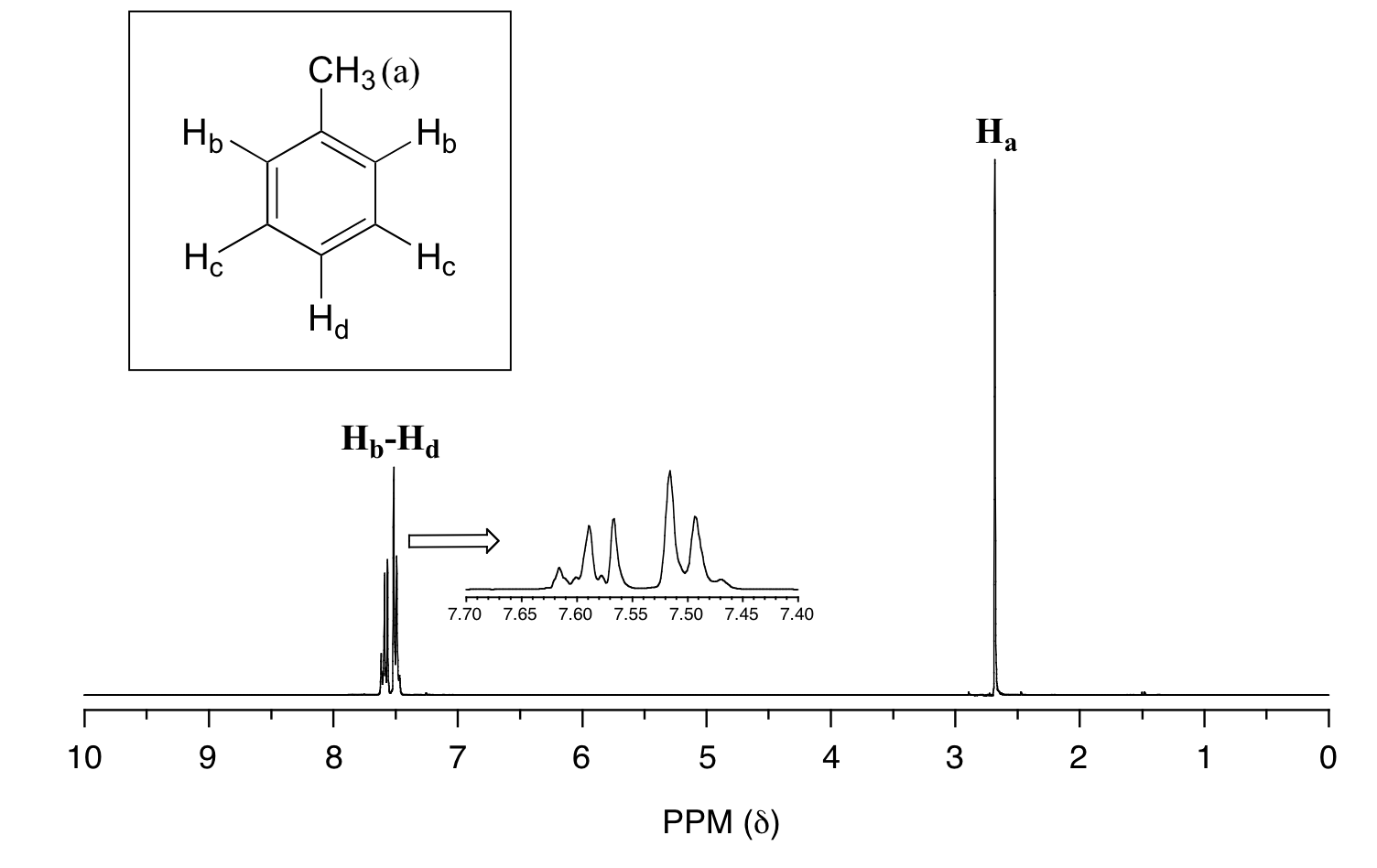
In practice, however, all three aromatic proton groups have very similar chemical shifts and their signals overlap substantially, making such detailed analysis difficult. In this case, we would refer to the aromatic part of the spectrum as a multiplet.
When we start trying to analyze complex splitting patterns in larger molecules, we gain an appreciation for why scientists are willing to pay large sums of money (hundreds of thousands of dollars) for higher-field NMR instruments. Quite simply, the stronger our magnet is, the more resolution we get in our spectrum. In a 100 MHz instrument (with a magnet of approximately 2.4 Tesla field strength), the 12 ppm frequency 'window' in which we can observe proton signals is 1200 Hz wide. In a 500 MHz (~12 Tesla) instrument, however, the window is 6000 Hz - five times wider. In this sense, NMR instruments are like digital cameras and HDTVs: better resolution means more information and clearer pictures (and higher price tags!)
Exercises
- Given the information below, draw the structures of compounds A through D.
- An unknown compound A was prepared as follows:
Mass spectrum:
base peak m/e = 39
parent peak m/e = 541H NMR spectrum:
δ (ppm) Relative Area Multiplicity 1.0 2 triplet 5.4 1 quintet - Unknown compound B has the molecular formula C7H6O2.
Infrared spectrum:
3200 cm−1 (broad) and 1747 cm−1 (strong) absorptions
1H NMR spectrum:
δ (ppm) Protons 6.9 2 7.4 2 9.8 1 10.9 1 Hint: Aromatic ring currents deshield all proton signals just outside the ring.
- Unknown compound C shows no evidence of unsaturation and contains only carbon and hydrogen.
Mass spectrum:
parent peak m/e = 68
1H NMR spectrum:
δ (ppm) Relative Area Multiplicity 1.84 3 triplet 2.45 1 septet Hint: Think three dimensionally!
- Unknown compound D (C15H14O) has the following spectral properties.
Infrared spectrum:
3010 cm−1 (medium)
1715 cm−1 (strong)
1610 cm−1 (strong)
1500 cm−1 (strong)1H NMR spectrum:
δ (ppm) Relative Area Multiplicity 3.00 2 triplet 3.07 2 triplet 7.1-7.9 10 Multiplets
- An unknown compound A was prepared as follows:
Answers
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)

