13.11: Spin-Spin Splitting in ¹H NMR Spectra
- Page ID
- 67297
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objectives
After completing this section, you should be able to
- explain the spin-spin splitting pattern observed in the 1H NMR spectrum of a simple organic compound, such as chloroethane or 2-bromopropane.
- interpret the splitting pattern of a given 1H NMR spectrum.
- determine the structure of a relatively simple organic compound, given its 1H NMR spectrum and other relevant information.
- use coupling constants to determine which groups of protons are coupling with one another in a 1H NMR spectrum.
- predict the splitting pattern which should be observed in the 1H NMR spectrum of a given organic compound.
Make certain that you can define, and use in context, the key terms below.
- coupling constant
- multiplet
- quartet
- triplet
- doublet
From what we have learned about 1H NMR spectra so far, we might predict that the spectrum of 1,1,2-trichloroethane, CHCl2CH2Cl, would consist of two peaks—one, at about 2.5-4.0 δ, expected for CH2-halogen compounds and one shifted downfield because of the presence of an additional electronegative chlorine atom on the second carbon. However, when we look at the spectrum it appears to be much more complex. True, we see absorptions in the regions we predicted, but these absorptions appear as a group of two peaks (a doublet) and a group of three peaks (a triplet). This complication, which may be disturbing to a student who longs for the simple life, is in fact very useful to the organic chemist, and adds greatly to the power of NMR spectroscopy as a tool for the elucidation of chemical structures. The split peaks (multiplets) arise because the magnetic field experienced by the protons of one group is influenced by the spin arrangements of the protons in an adjacent group.
Spin-spin coupling is often one of the more challenging topics for organic chemistry students to master. Remember the n + 1 rule and the associated coupling patterns.
The source of spin-spin coupling
The 1H-NMR spectra that we have seen so far (of methyl acetate and para-xylene) are somewhat unusual in the sense that in both of these molecules, each set of protons generates a single NMR signal. In fact, the 1H-NMR spectra of most organic molecules contain proton signals that are 'split' into two or more sub-peaks. Rather than being a complication, however, this splitting behavior actually provides us with more information about our sample molecule.
Consider the spectrum for 1,1,2-trichloroethane. In this and in many spectra to follow, we show enlargements of individual signals so that the signal splitting patterns are recognizable.
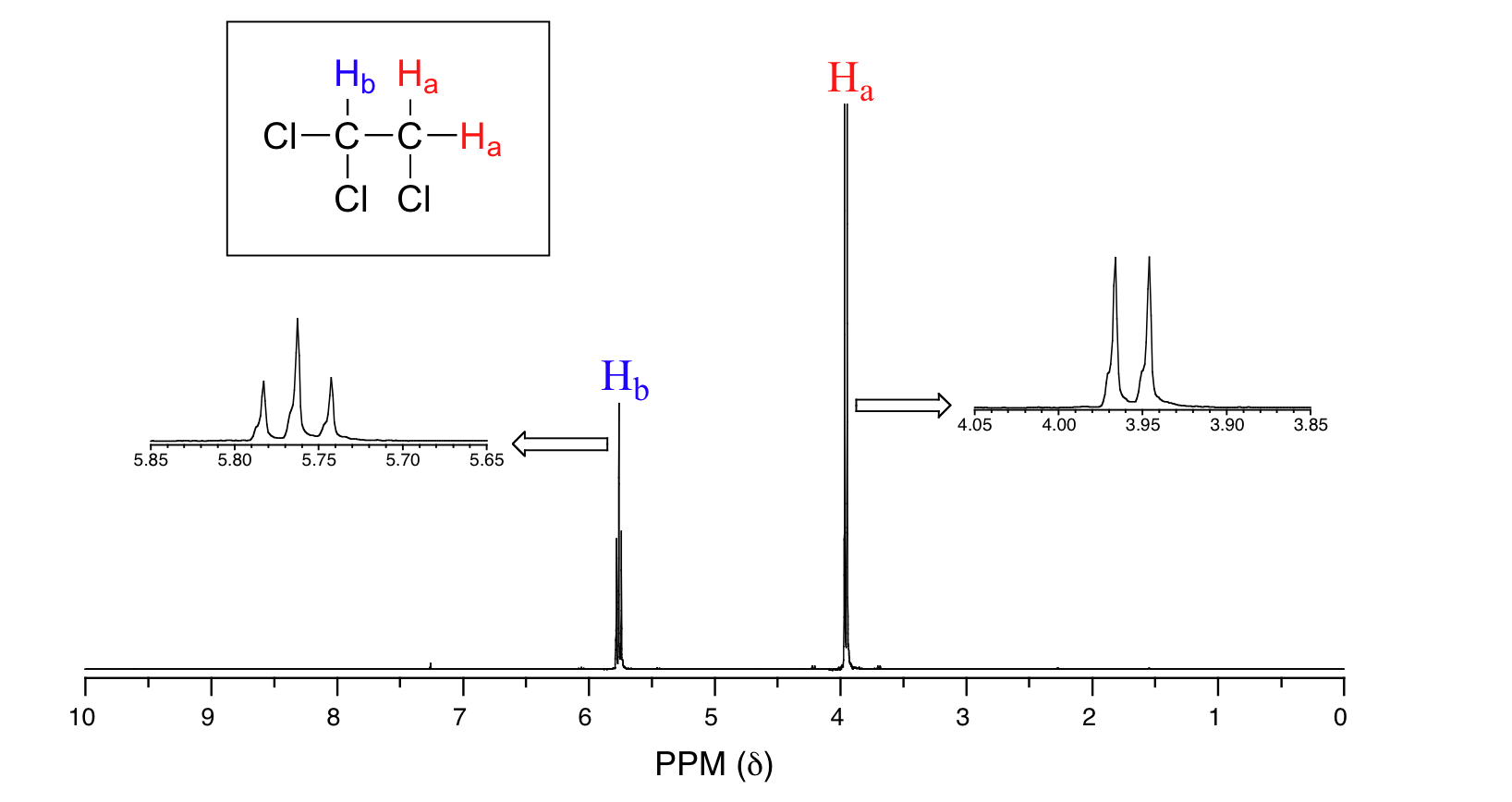
The signal at 3.96 ppm, corresponding to the two Ha protons, is split into two subpeaks of equal height (and area) – this is referred to as a doublet. The Hb signal at 5.76 ppm, on the other hand, is split into three sub-peaks, with the middle peak higher than the two outside peaks - if we were to integrate each subpeak, we would see that the area under the middle peak is twice that of each of the outside peaks. This is called a triplet.
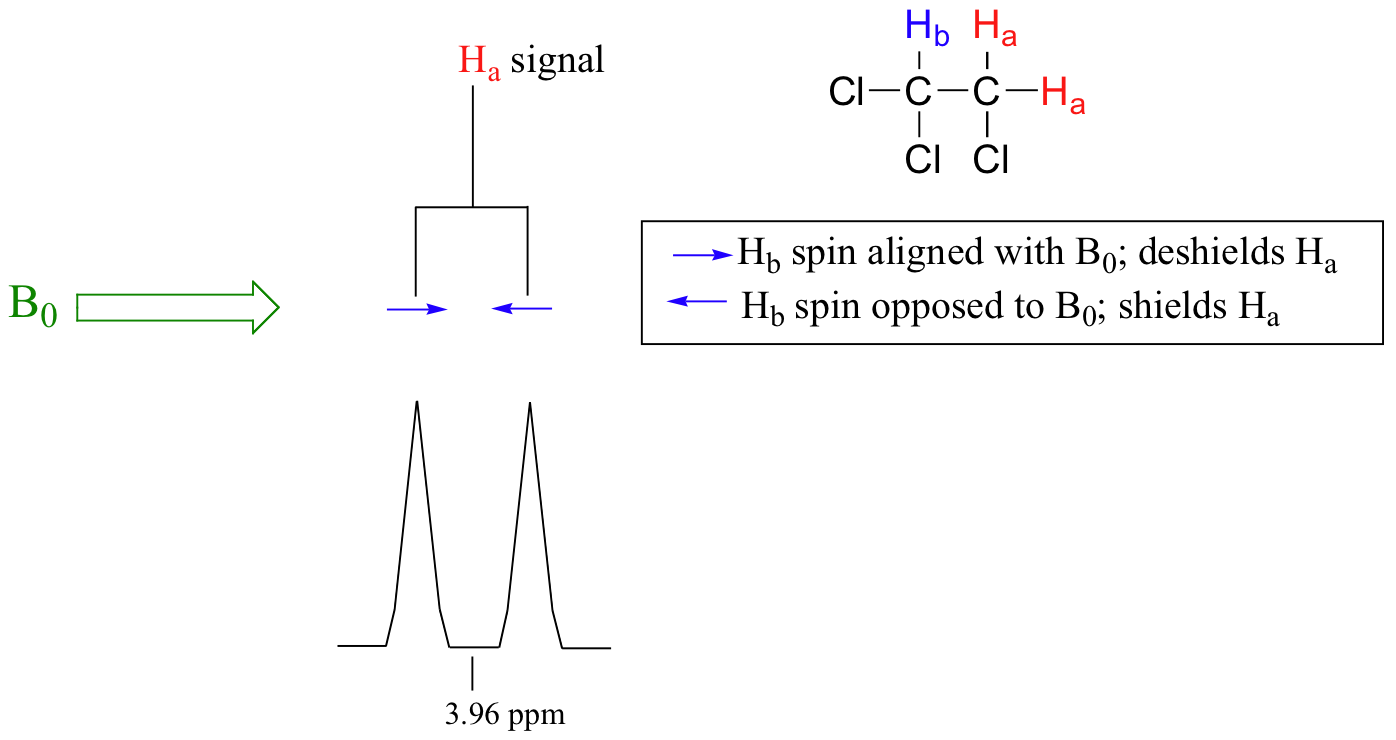
The source of signal splitting is a phenomenon called spin-spin coupling, a term that describes the magnetic interactions between neighboring, non-equivalent NMR-active nuclei. In our 1,1,2 trichloromethane example, the Ha and Hb protons are spin-coupled to each other. Here's how it works, looking first at the Ha signal: in addition to being shielded by nearby valence electrons, each of the Ha protons is also influenced by the small magnetic field generated by Hb next door (remember, each spinning proton is like a tiny magnet). The magnetic moment of Hb will be aligned with B0 in (slightly more than) half of the molecules in the sample, while in the remaining half of the molecules it will be opposed to B0. The Beff ‘felt’ by Ha is a slightly weaker if Hb is aligned against B0, or slightly stronger if Hb is aligned with B0. In other words, in half of the molecules Ha is shielded by Hb (thus the NMR signal is shifted slightly upfield) and in the other half Ha is deshielded by Hb(and the NMR signal shifted slightly downfield). What would otherwise be a single Ha peak has been split into two sub-peaks (a doublet), one upfield and one downfield of the original signal. These ideas an be illustrated by a splitting diagram, as shown below.
Now, let's think about the Hbsignal. The magnetic environment experienced by Hb is influenced by the fields of both neighboring Ha protons, which we will call Ha1 and Ha2. There are four possibilities here, each of which is equally probable. First, the magnetic fields of both Ha1 and Ha2 could be aligned with B0, which would deshield Hb, shifting its NMR signal slightly downfield. Second, both the Ha1 and Ha2 magnetic fields could be aligned opposed to B0, which would shield Hb, shifting its resonance signal slightly upfield. Third and fourth, Ha1 could be with B0 and Ha2 opposed, or Ha1opposed to B0 and Ha2 with B0. In each of the last two cases, the shielding effect of one Ha proton would cancel the deshielding effect of the other, and the chemical shift of Hb would be unchanged.
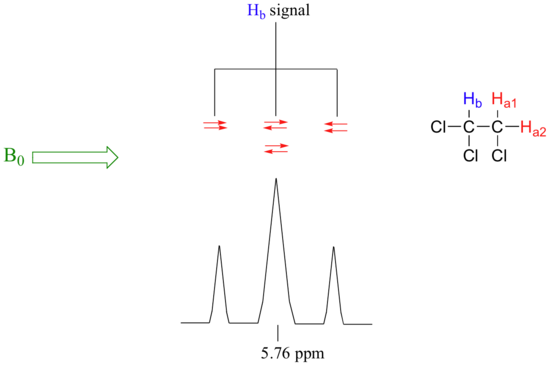
So in the end, the signal for Hb is a triplet, with the middle peak twice as large as the two outer peaks because there are two ways that Ha1 and Ha2 can cancel each other out.
Now, consider the spectrum for ethyl acetate:

We see an unsplit 'singlet' peak at 1.833 ppm that corresponds to the acetyl (Ha) hydrogens – this is similar to the signal for the acetate hydrogens in methyl acetate that we considered earlier. This signal is unsplit because there are no adjacent hydrogens on the molecule. The signal at 1.055 ppm for the Hc hydrogens is split into a triplet by the two Hb hydrogens next door. The explanation here is the same as the explanation for the triplet peak we saw previously for 1,1,2-trichloroethane.
The Hbhydrogens give rise to a quartet signal at 3.915 ppm – notice that the two middle peaks are taller then the two outside peaks. This splitting pattern results from the spin-coupling effect of the three Hc hydrogens next door, and can be explained by an analysis similar to that which we used to explain the doublet and triplet patterns.
- Explain, using left and right arrows to illustrate the possible combinations of nuclear spin states for the Hc hydrogens, why the Hb signal in ethyl acetate is split into a quartet.
- The integration ratio of doublets is 1:1, and of triplets is 1:2:1. What is the integration ratio of the Hb quartet in ethyl acetate? (Hint – use the illustration that you drew in part a to answer this question.)
- Answer
-
a)
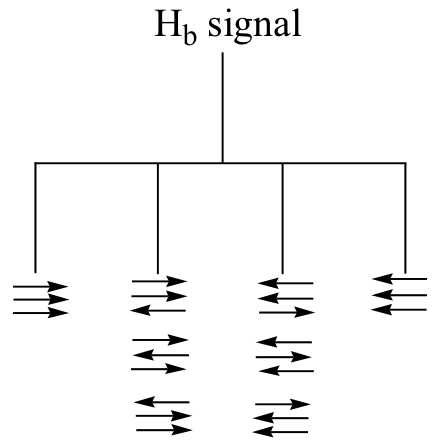
b) The figure above demonstrates that the quartet subpeaks integrate to 1:3:3:1 (eg., there are three ways for two spins to be aligned with B0 and one against B0). As an analogy, if you flip three coins at once, you have a 1 in eight chance of getting all heads, 1 in 8 chance of all tails, a 3 in 8 chance of two heads and a tail, and a 3 in 8 chance of two tails and a head.
By now, you probably have recognized the pattern which is usually referred to as the n + 1 rule: if a set of hydrogens has n neighboring, non-equivalent hydrogens, it will be split into n + 1 subpeaks. Thus the two Hb hydrogens in ethyl acetate split the Hc signal into a triplet, and the three Hc hydrogens split the Hb signal into a quartet. This is very useful information if we are trying to determine the structure of an unknown molecule: if we see a triplet signal, we know that the corresponding hydrogen or set of hydrogens has two `neighbors`. When we begin to determine structures of unknown compounds using 1H-NMR spectral data, it will become more apparent how this kind of information can be used.
Three important points need to be emphasized here. First, signal splitting only occurs between non-equivalent hydrogens – in other words, Ha1 in 1,1,2-trichloroethane is not split by Ha2, and vice-versa.

Second, splitting occurs primarily between hydrogens that are separated by three bonds. This is why the Ha hydrogens in ethyl acetate form a singlet– the nearest hydrogen neighbors are five bonds away, too far for coupling to occur.
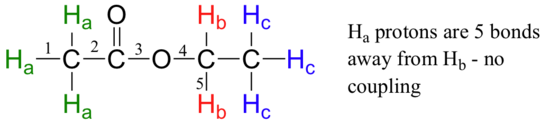
Occasionally we will see four-bond and even 5-bond splitting, but in these cases the magnetic influence of one set of hydrogens on the other set is much more subtle than what we typically see in three-bond splitting (more details about how we quantify coupling interactions is provided in section 5.5B). Finally, splitting is most noticeable with hydrogens bonded to carbon. Hydrogens that are bonded to heteroatoms (alcohol or amino hydrogens, for example) are coupled weakly - or not at all - to their neighbors. This has to do with the fact that these protons exchange rapidly with solvent or other sample molecules.
Below are a few more examples of chemical shift and splitting pattern information for some relatively simple organic molecules.

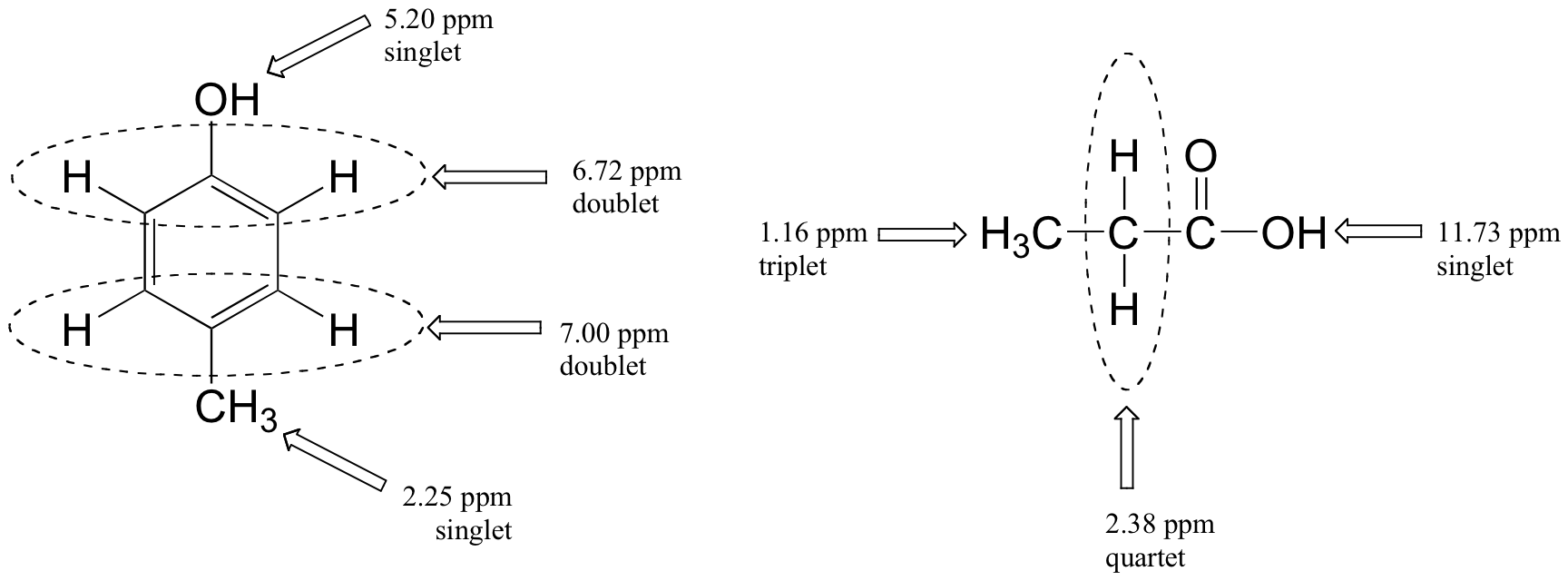
Multiplicity in Proton NMR
The number of lines in a peak is always one more (n+1) than the number of hydrogens on the neighboring carbon. This table summarizes coupling patterns that arise when protons have different numbers of neighbors.
| # of lines | ratio of lines | term for peak | # of neighbors |
| 1 | - | singlet | 0 |
| 2 | 1:1 | doublet | 1 |
| 3 | 1:2:1 | triplet | 2 |
| 4 | 1:3:3:1 | quartet | 3 |
| 5 | 1:4:6:4:1 | quintet | 4 |
| 6 | 1:5:10:10:5:1 | sextet | 5 |
| 7 | 1:6:15:20:15:6:1 | septet | 6 |
| 8 | 1:7:21:35:35:21:7:1 | octet | 7 |
| 9 | 1:8:28:56:70:56:28:8:1 | nonet | 8 |
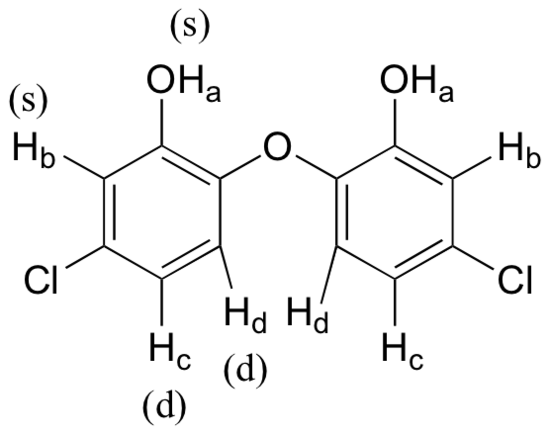
How many proton signals would you expect to see in the 1H-NMR spectrum of the structure shown below? For each of the proton signals, predict the splitting pattern. Assume that you see only 3-bond coupling.
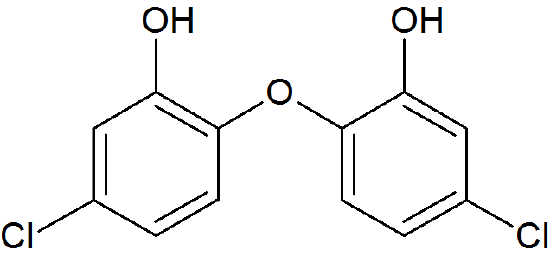
- Answer
-
Because of the symmetry in the molecule, there are only four proton signals. Predicted splitting is indicated.
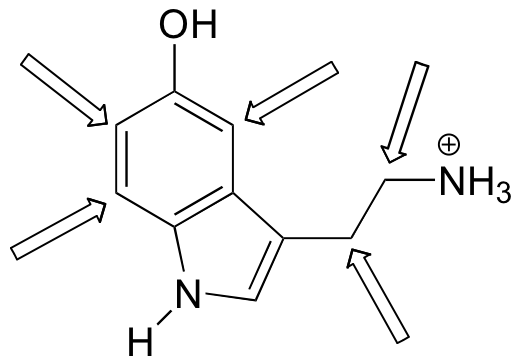
Predict the splitting pattern for the 1H-NMR signals corresponding to the protons at the locations indicated by arrows (the structure is that of the neurotransmitter serotonin).
- Answer
-
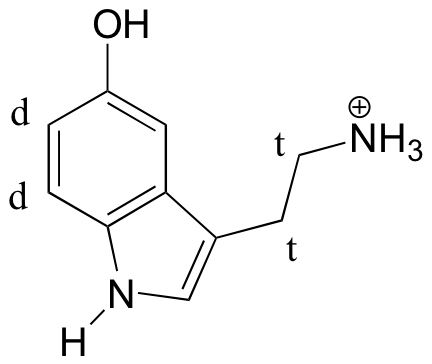
(recall that splitting is generally not seen with protons on heteroatoms)
Coupling constants
Chemists quantify the spin-spin coupling effect using something called the coupling constant, which is abbreviated with the capital letter J. The coupling constant is simply the difference, expressed in Hz, between two adjacent sub-peaks in a split signal. For our doublet in the 1,1,2-trichloroethane spectrum, for example, the two subpeaks are separated by 6.1 Hz, and thus we write 3Ja-b = 6.1 Hz.
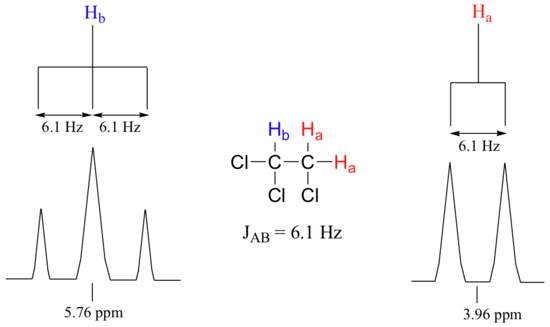
The superscript 3 tells us that this is a three-bond coupling interaction, and the a-b subscript tells us that we are talking about coupling between Ha and Hb. Unlike the chemical shift value, the coupling constant, expressed in Hz, is the same regardless of the applied field strength of the NMR magnet. This is because the strength of the magnetic moment of a neighboring proton, which is the source of the spin-spin coupling phenomenon, does not depend on the applied field strength.
When we look closely at the triplet signal in 1,1,2-trichloroethane, we see that the coupling constant - the `gap` between subpeaks - is 6.1 Hz, the same as for the doublet. This is an important concept! The coupling constant 3Ja-b quantifies the magnetic interaction between the Ha and Hb hydrogen sets, and this interaction is of the same magnitude in either direction. In other words, Ha influences Hb to the same extent that Hb influences Ha. When looking at more complex NMR spectra, this idea of reciprocal coupling constants can be very helpful in identifying the coupling relationships between proton sets.
Coupling constants between proton sets on neighboring sp3-hybridized carbons is typically in the region of 6-8 Hz. With protons bound to sp2-hybridized carbons, coupling constants can range from 0 Hz (no coupling at all) to 18 Hz, depending on the bonding arrangement.

For vinylic hydrogens in a trans configuration, we see coupling constants in the range of 3J = 11-18 Hz, while cis hydrogens couple in the 3J = 6-15 Hz range. The 2-bond coupling between hydrogens bound to the same alkene carbon (referred to as geminal hydrogens) is very fine, generally 5 Hz or lower. Ortho hydrogens on a benzene ring couple at 6-10 Hz, while 4-bond coupling of up to 4 Hz is sometimes seen between meta hydrogens.
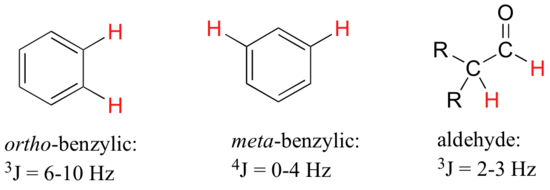
Fine (2-3 Hz) coupling is often seen between an aldehyde proton and a three-bond neighbor. Table 4 lists typical constant values.
Exercises
Predict the splitting patterns of the following molecules.

- Answer
-
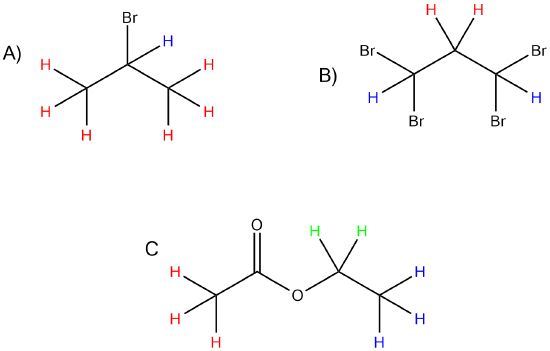
A. H: Doublet. H: Septet
B. H: Triplet, H: Triplet
C. H: Singlet, H: Quartet, H: Triplet
Draw the following according to the criteria given.
A. C3H5O; two triplet, 1 doublet
B. C4H8O2; three singlets
C. C5H12; one singlet
- Answer
-
These are just some drawings, more may be possible.
.png?revision=1&size=bestfit&width=516&height=277)
The following spectrum is for C3H8O. Determine the structure.
A; triplet, B; Singlet, C; Sextet, D; Triplet
.png?revision=1)
- Answer
-
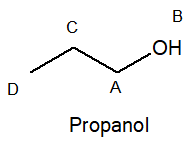.png?revision=1)
Note: Remember, chemically equivalent protons do not couple with one another to give spin-spin splitting.
Contributors and Attributions
Dr. Dietmar Kennepohl FCIC (Professor of Chemistry, Athabasca University)
Prof. Steven Farmer (Sonoma State University)
Organic Chemistry With a Biological Emphasis by Tim Soderberg (University of Minnesota, Morris)
Chris P Schaller, Ph.D., (College of Saint Benedict / Saint John's University)

