13.7: Intermolecular Forces

⚙️ Learning Objectives

• To describe the intermolecular forces in molecules. 

The properties of liquids are intermediate between those of gases and solids, but are more similar to solids. In contrast to intramolecular forces, such as the covalent bonds that hold atoms together in molecules and polyatomic ions, intermolecular forces hold molecules together in a liquid or solid. Intermolecular forces are generally much weaker than covalent bonds. Given the large difference in the strengths of intramolecular and intermolecular forces, changes between the solid, liquid, and gaseous states almost invariably occur for molecular substances without breaking covalent bonds.

Intermolecular forces determine bulk properties, such as the melting points of solids and the boiling points of liquids. Liquids boil when the molecules have enough thermal energy to overcome the attractive intermolecular forces that hold them together, thereby forming bubbles of vapor within the liquid. Similarly, solids melt when the molecules acquire enough thermal energy to overcome the intermolecular forces that lock them into place in the solid.

In this section, we explicitly consider three kinds of intermolecular interactions, the first two of which are often described collectively as van der Waals forces. There are two additional types of electrostatic interactions: the ion–ion interactions that are responsible for ionic bonding with which you are already familiar, and the ion–dipole interactions that occur when ionic substances dissolve in a polar substance such as water which was introduced in the previous section and will be discussed more in the next chapter.

Dipole-Dipole Forces

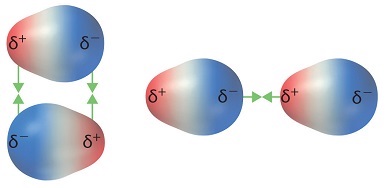
As previously described, polar molecules have one end that is partially positive (δ+) and another end that is partially negative (δ–). Because molecules in a liquid move freely and continuously, molecules experience both attractive and repulsive forces while interacting with each other. Polar molecules tend to align themselves so that the positive end of one dipole is near the negative end of a different dipole and vice versa, as shown in Figure \(\PageIndex{1}\). These predominant attractive intermolecular forces between polar molecules are called dipole–dipole forces.
 

     

Figure \(\PageIndex{1}\): Dipole-dipole forces involve molecular orientations in which the positive end of one dipole (δ⁺) is near the negative end of another (δ⁻) of a different dipole, causing an attraction between the two molecules. (Animation adapted from Wisc-Online, licensed by CC BY-NC-SA)

The attraction between partially positive and partially negative regions of a polar molecule that makes up dipole-dipole forces is the same type of attraction that occurs between cations and anions in an ionic compound. However, because each end of a dipole possesses only a fraction of the charge of an electron, dipole–dipole forces are substantially weaker than the forces between two ions, each of which has a charge of at least ±1, or between a dipole and an ion, in which one of the species has at least a full positive or negative charge. In addition, the attractive interaction between dipoles falls off much more rapidly with increasing distance than do the ion–ion interactions. Thus a substance such as HCl, which is partially held together by dipole–dipole interactions, is a gas at room temperature and 1 atm pressure. Conversely, NaCl, which is held together by interionic interactions, is a high-melting-point solid. Within a series of compounds of similar molar mass, the strength of the intermolecular interactions increases as the polarity of the molecules increases. This increase in the strength of the intermolecular interaction is reflected in an increase in melting point or boiling point, as shown in Table \(\PageIndex{1}\).
 

Table \(\PageIndex{1}\): Relationships Between the Polarity and Boiling Point for Organic Compounds of Similar Molar Mass

Compound	Molar Mass (g/mol)	*Dipole Moment (D)	Boiling Point (K)
C3H6 (cyclopropane)	42	0	240
CH3OCH3 (dimethyl ether)	46	1.30	248
CH3CN (acetonitrile)	41	3.9	355

*The dipole moment is a measure of molecular polarity. The larger the numeric value, the greater the polarity of the molecule.

London Dispersion Forces

Thus far, we have considered only interactions between polar molecules. Other factors must be considered to explain why many nonpolar molecules, such as bromine, benzene, and hexane, are liquids at room temperature and why others, such as iodine and naphthalene, are solids. Even the noble gases can be liquefied or solidified at low temperatures, high pressures, or both. What kind of attractive forces can exist between nonpolar molecules or atoms? This question was answered by Fritz London (1900–1954), a German physicist who later worked in the United States. In 1930, London proposed that temporary fluctuations in the electron distributions within atoms and nonpolar molecules could result in the formation of short-lived instantaneous dipole moments, which produce attractive forces called London dispersion forces, or simply London forces or dispersion forces, between otherwise nonpolar substances.

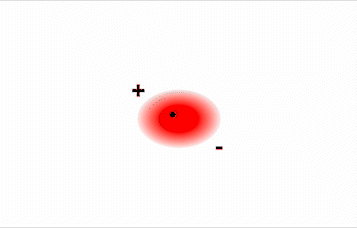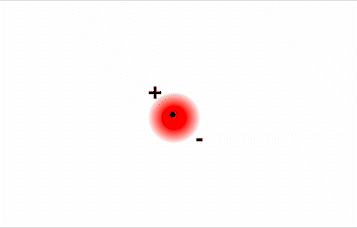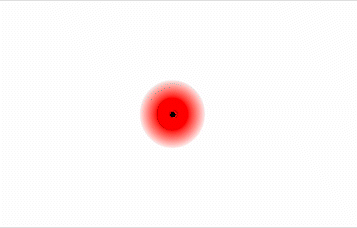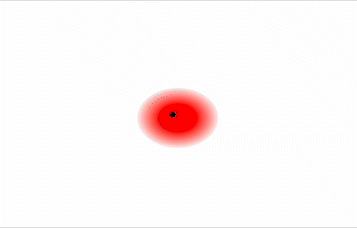
Consider a pair of adjacent He atoms, for example. On average, the two electrons in each He atom are uniformly distributed around the nucleus. Because the electrons are in constant motion, however, their distribution in one atom is likely to be asymmetrical at any given instant, resulting in an instantaneous dipole moment (see image on left in Figure \(\PageIndex{2}\) below). The instantaneous dipole moment on one atom can interact with the electrons in an adjacent atom, pulling them toward the positive end of the instantaneous dipole or repelling them from the negative end (see image on right in Figure \(\PageIndex{2}\) below). The net effect is that the first atom causes the temporary formation of a dipole, called an induced dipole, in the second. Interactions between these temporary dipoles cause atoms to be attracted to one another. These attractive interactions are weak and fall off rapidly with increasing distance. 
 

          

Figure \(\PageIndex{2}\): Instantaneous dipole moments. The formation of an instantaneous dipole moment on a He atom results in the formation of an induced dipole on an adjacent atom or molecule. The resulting temporary attractions are called dispersion forces. (Animation adapted from Wisc-Online, licensed by CC BY-NC-SA)

Dispersion forces between nonpolar molecules can produce intermolecular attractions just as they produce interatomic attractions in monatomic substances like He. This effect tends to become more pronounced as atomic and molecular masses increase (Table \(\PageIndex{2}\)). For example, Xe boils at −108.1°C, whereas He boils at −269°C. The reason for this trend is that the strength of dispersion forces is related to the ease with which the electron distribution in a given atom can become temporarily asymmetrical. In small atoms such as He, its two electrons are held close to the nucleus in a very small volume, and electron-electron repulsions are strong enough to prevent significant asymmetry in their distribution. In larger atoms such as Xe, there are many more electrons and energy shells. As a result, it is relatively easy to temporarily deform the electron distribution to generate an instantaneous or induced dipole, since there is a greater probability of a temporary, uneven distribution of electrons.
 

Table \(\PageIndex{2}\): Normal Melting and Boiling Points of Some Elements and Nonpolar Compounds

Substance	Molar Mass (g/mol)	Melting Point (°C)	Boiling Point (°C)
Ar	40	−189.4	−185.9
Xe	131	−111.8	−108.1
N2	28	−210	−195.8
O2	32	−218.8	−183.0
F2	38	−219.7	−188.1
I2	254	113.7	184.4
CH4	16	−182.5	−161.5
CCl4	154	−22.2	76.7

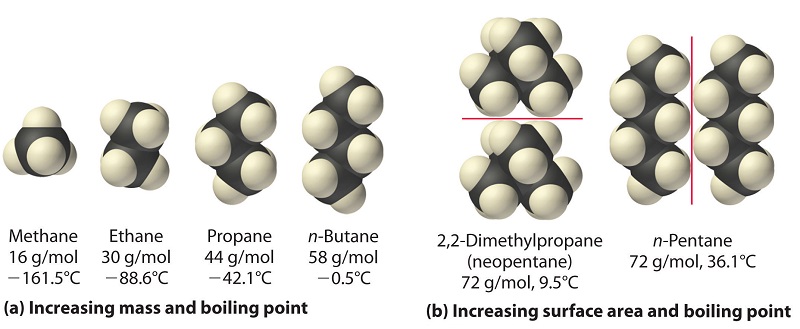
Thus, dispersion forces are responsible for the general trend toward higher boiling points with increased molecular mass and greater surface area in a homologous series of compounds, such as the alkanes in Figure \(\PageIndex{3}\)(a) below. The strengths of dispersion forces also depend significantly on molecular shape because shape determines how much of one molecule can interact with its neighboring molecules at any given time. For example, Figure \(\PageIndex{3}\)(b) shows 2,2-dimethylpropane and pentane, both of which have the empirical formula C₅H₁₂. 2,2-dimethylpropane is almost spherical, with a small surface area for intermolecular interactions, whereas pentane has an extended conformation that enables it to come into close contact with other pentane molecules. As a result, the boiling point of 2,2-dimethylpropane (9.5°C) is more than 25°C lower than the boiling point of pentane (36.1°C).
 

Figure \(\PageIndex{3}\): Mass and surface area affect the strength of dispersion forces. (a) In this series of four simple alkanes, larger molecules have stronger disperson forces between them than smaller molecules and have higher boiling points. (b) Linear pentane molecules have a larger surface area and stronger intermolecular forces than spherical neopentane molecules. As a result, 2,2-dimethylpropane is a gas at room temperature, whereas pentane is a volatile liquid.

Finally, it should be noted that all molecules, whether polar or nonpolar, are attracted to one another by dispersion forces in addition to any other attractive forces that may be present. In general, however, dipole–dipole forces in small polar molecules are significantly stronger than dispersion forces, so the dipole–dipole forces predominate.

Hydrogen Bonds

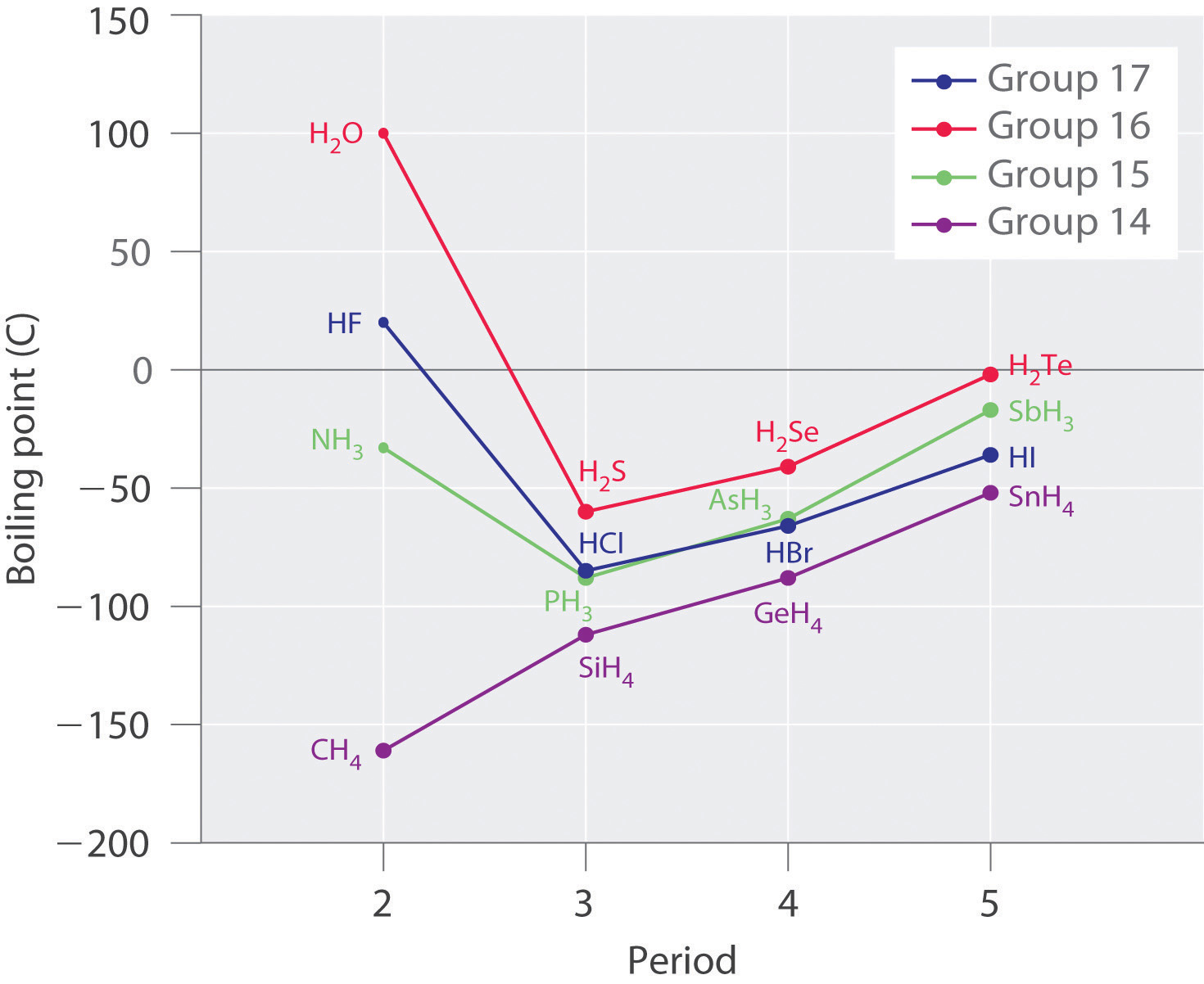
Let's apply what we have learned to the boiling points of the covalent hydrides of elements in Groups 14-17, as shown in Figure \(\PageIndex{4}\) below. Methane and the other hydrides of Group 14 elements are symmetrical molecules and are therefore nonpolar. Thus, the only attractive forces between molecules will be dispersion forces. These dispersion forces are expected to become stronger as the molar mass of the compound increases. The increasing strength of the dispersion forces will cause the boiling point of the compounds to increase, which is what is observed.

In Groups 15-17, lone pairs are present on the central atom, creating asymmetry in the molecules. The molecules are therefore polar to varying degrees and will contain dipole-dipole forces in addition to the dispersion forces. The presence of the stronger dipole-dipole force causes the boiling points of molecules in Groups 15-17 to be greater than the boiling point of the molecules in Group 14 in the same period. We can still see that the boiling point increases with molar mass due to increases in the strength of the dispersion forces as we move from period 3 to period 5. 

The trends break down for the hydrides of the lightest members of groups 15–17 which have boiling points that are more than 100°C greater than predicted on the basis of their molar masses. The effect is most dramatic for water: if we extend the straight line connecting the points for H₂Te and H₂Se to the line for period 2, we obtain an estimated boiling point of −70°C for water! Imagine the implications for life on Earth if water boiled at −70°C rather than 100°C. Obviously, there must be some other attractive force present in NH₃, HF, and H₂O to account for the higher boiling points in these molecules. This attractive force is known as a hydrogen bond.
 

Figure \(\PageIndex{4}\): The effects of hydrogen bonding on boiling points. These plots of the boiling points of the covalent hydrides of the elements of groups 14–17 show that the boiling points of the lightest members of each series for which hydrogen bonding is possible (NH₃, HF, and H₂O) are anomalously high for compounds with such low molecular masses.

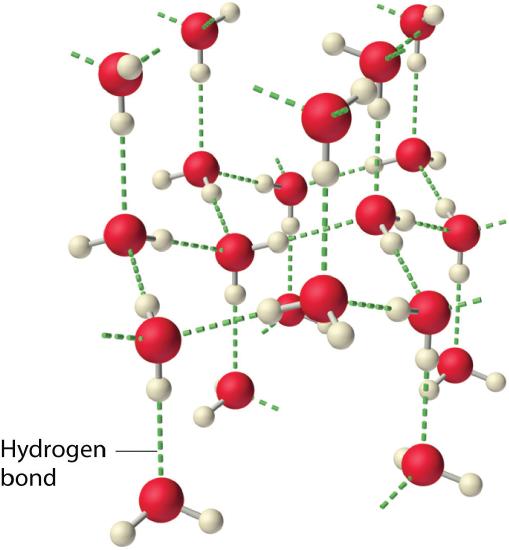
Hydrogen bonds are an unusually strong version of dipole–dipole forces in which hydrogen atoms are bonded to highly electronegative atoms such as N, O, and F. In addition, the N, O, or F will typically have lone pair electrons on the atom in the Lewis structure. The large difference in electronegativity results in a large partial positive charge on hydrogen and a correspondingly large partial negative charge on the N, O, or F atom which will be concentrated on the lone pair electrons. Consequently, H—N, H—O, and H—F bonds will have very large bond dipoles, allowing the H atoms to interact strongly with the lone pairs of N, O, or F atoms on neighboring molecules. In addition, because the atoms involved are so small, these molecules can also approach one another more closely than most other dipoles. The combination of large bond dipoles and short intermolecular distances results in very strong dipole–dipole interactions called hydrogen bonds, as shown for ice in Figure \(\PageIndex{5}\).

Because it is such a strong intermolecular attraction, a hydrogen bond is usually indicated by a dotted line between the hydrogen atom attached to N, O, or F and the atom that has the lone pair of electrons. One thing that you may notice is that the hydrogen bond in the ice in Figure \(\PageIndex{5}\) is drawn to where the lone pair electrons are found on the oxygen atom. This is because the large partial negative charge on the oxygen atom (or on a N or F atom) is concentrated in the lone pair electrons. Thus, the hydrogen bond attraction will be specifically between the lone pair electrons on the N, O, or F atom and the H of a neighboring molecule. Because each water molecule contains two hydrogen atoms and two lone pairs, it can make up to four hydrogen bonds with adjacent water molecules.

In order to maximize the hydrogen bonding when fixed in position as a solid, the molecules in ice adopt a tetrahedral arrangement. Each oxygen atom is surrounded by a distorted tetrahedron of hydrogen atoms that form bridges to the oxygen atoms of adjacent water molecules. The resulting open, cage-like structure of ice means that the solid is actually slightly less dense than the liquid, which explains why ice floats on water, rather than sinks. The structure of liquid water is very similar, but in the liquid, the hydrogen bonds are continually broken and formed because of rapid molecular motion so that the tetrahedral arrangement is not maintained.
 

Figure \(\PageIndex{5}\) (left to right): The hydrogen-bonded structure of ice. The Lewis structure of H₂O, including lone pairs, superimposed over its three-dimensional rendering.

Because ice is less dense than liquid water, rivers, lakes, and oceans freeze from the top down. In fact, the ice forms a protective surface layer that insulates the rest of the water, allowing fish and other organisms to survive in the lower levels of a frozen lake or sea. If ice were denser than the liquid, the ice formed at the surface in cold weather would sink as fast as it formed. Bodies of water would freeze from the bottom up, which would be lethal for most aquatic creatures. The expansion of water when freezing also explains why automobile or boat engines must be protected by “antifreeze” and why unprotected pipes in houses break if they are allowed to freeze.
 

✅ Example \(\PageIndex{1}\)

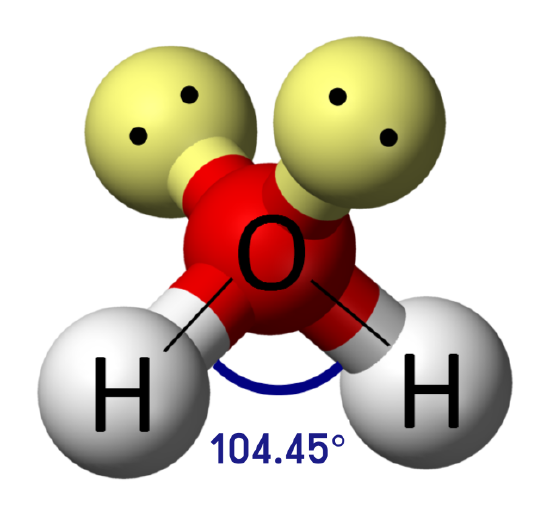
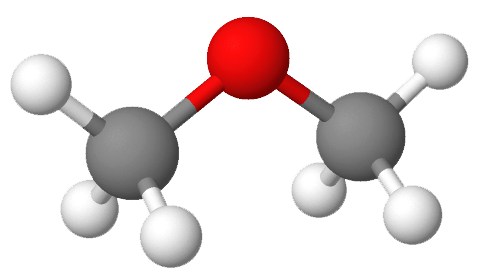
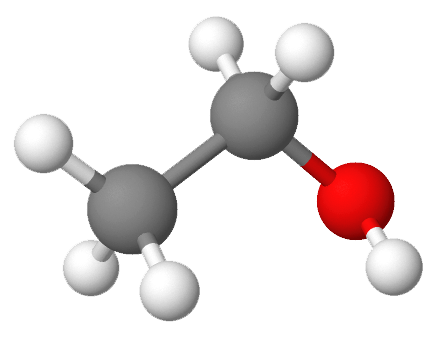
Which substance(s) can form a hydrogen bond to another molecule of itself? If the substance cannot form a hydrogen bond to another molecule of itself, which intermolecular force is the predominant intermolecular force for the substance?

       

        

Solution

Considering the structures from left to right:

1. This molecule cannot form hydrogen bonds to another molecule of itself since there are no H atoms directly bonded to N, O, or F. However, the molecule is polar, meaning that dipole-dipole forces are present. While all molecules, polar or nonpolar, have dispersion forces, the dipole-dipole forces are predominant.
        
2. This molecule cannot form hydrogen bonds to another molecule of itself since there are no H atoms directly bonded to N, O, or F. The molecule is nonpolar, meaning that the only intermolecular forces present are dispersion forces. This means that dispersion forces are also the predominant intermolecular force.
        
3. This molecule can form hydrogen bonds to another molecule of itself since there is an H atom directly bonded to O in the hydroxyl group (—OH).

 

✅ Example \(\PageIndex{2}\)

Arrange the substances shown in Example \(\PageIndex{1}\) above in order of decreasing boiling point.

Solution

Considering the structures in Example \(\PageIndex{1}\) from left to right, the condensed structural formulas and molar masses are:

• CH₃OCH₃ (46 g/mol), CH₃CH₂CH₃ (44 g/mol), and CH₃CH₂OH (46 g/mol).

Since they all have about the same molar mass, their boiling points should decrease in the order of the strongest to weakest predominant intermolecular force. Therefore, their arrangement in order of decreasing boiling point is:

 > 

 > 

 

✏️ Exercise \(\PageIndex{1}\)

Which intermolecular forces are present in each substance? If there is more than one, identify the predominant intermolecular force in each substance.

1. HF
2. H₂
3. HBr

Answer A

Dispersion forces, dipole-dipole forces, hydrogen bonds are all present. Hydrogen bonds are the predominant intermolecular force. 

Answer B

Dispersion forces are the only intermolecular forces present. Therefore, they are also the predominant intermolecular force.

Answer C

Dispersion forces and dipole-dipole forces are present. Dipole-dipole forces are the predominant intermolecular force. 

 

✏️ Exercise \(\PageIndex{2}\)

Arrange the noble gases (He, Ne, Ar, Kr, and Xe) in order of increasing boiling point.

Answer

He < Ne < Ar < Kr < Xe (This is in the order of increasing molar mass, since the only intermolecular forces present for each are dispersion forces.)

Summary

Click "Next" to begin a short review of this section.

Source: Wisc-Online, licensed by CC BY-NC-SA

 

 

---

This page is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Lance S. Lund (Anoka-Ramsey Community College) and Vicki MacMurdo (Anoka-Ramsey Community College).