14.3: Aqueous Solutions of Solids

Last updated
Save as PDF

Page ID: 289454

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

⚙️ Learning Objectives

Define electrolytes and nonelectrolytes.
Explain why solutions form.
Discuss the idea of water as the "universal solvent."
Explain how water molecules attract ionic solids when they dissolve in water.
Use solubility curves to determine that saturation of a solution.

We have learned that solutions can be formed in a variety of combinations using solids, liquids, and gases. But how, exactly, do solutions form? Why is it that oil and water will not form a solution, and yet vinegar and water will? Why could we dissolve table salt in water, but not in vegetable oil? The reasons why solutions will form will be explored in this section, along with a discussion of why water is used most frequently to dissolve substances of various types.

Electrolyte Solutions: Dissolved Ionic Solids

When some substances are dissolved in water, they undergo a physical or chemical change that yields ions in solution. These substances constitute an important class of compounds called electrolytes. Substances that do not yield ions when dissolved are called nonelectrolytes. If the physical or chemical process that generates the ions is close to 100% efficient (all of the dissolved compound yields ions), then the substance is known as a strong electrolyte (good conductor of electricity). If only a relatively small fraction of the dissolved substance yields ions, the substance is a weak electrolyte (weak conductor of electricity).

Substances may be identified as strong electrolytes, weak electrolytes, or nonelectrolytes by measuring the electrical conductance of an aqueous solution containing the substance. To conduct electricity, a substance must contain freely mobile, charged species. Most familiar is the conduction of electricity through metallic wires, in which case the mobile, charged entities are electrons. Solutions may also conduct electricity if they contain dissolved ions, with conductivity increasing as ion concentration increases. Applying a voltage to electrodes immersed in a solution permits assessment of the relative concentration of dissolved ions, either quantitatively, by measuring the electrical current flow, or qualitatively, by observing the brightness of a light bulb included in the circuit (Figure \(\PageIndex{1}\)).

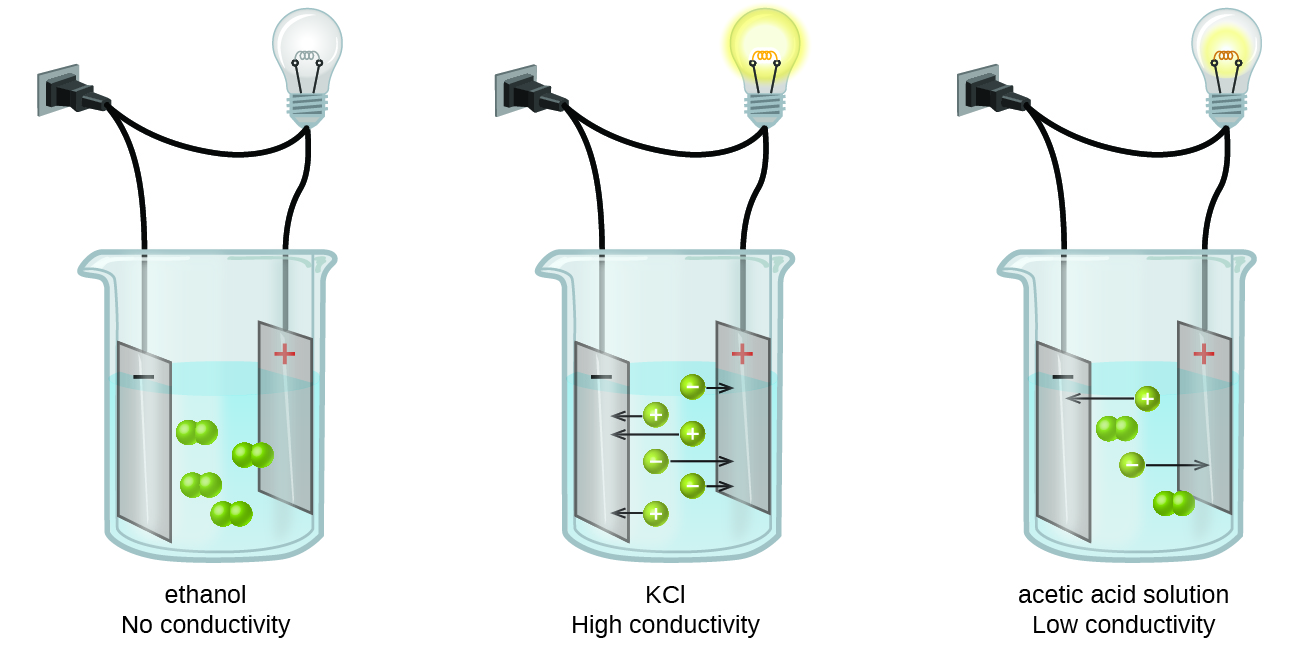
This diagram shows three separate beakers. Each has a wire plugged into a wall outlet. In each case, the wire leads from the wall to the beaker and is split resulting in two ends. One end leads to a light bulb and continues on to a rectangle labeled with a plus sign. The other end leads to a rectangle labeled with a minus sign. The rectangles are in a solution. In the first beaker, labeled “Ethanol No Conductivity,” four pairs of linked small green spheres suspended in the solution between the rectangles. In the second beaker, labeled “KCl Strong Conductivity,” six individual green spheres, three labeled plus and three labeled minus are suspended in the solution. Each of the six spheres has an arrow extending from it pointing to the rectangle labeled with the opposite sign. In the third beaker, labeled “Acetic acid solution Weak conductivity,” two pairs of joined green spheres and two individual spheres, one labeled plus and one labeled minus are shown suspended between the two rectangles. The plus labeled sphere has an arrow pointing to the rectangle labeled minus and the minus labeled sphere has an arrow pointing to the rectangle labeled plus. — Figure \(\PageIndex{1}\): Solutions of nonelectrolytes, such as ethanol, do not contain dissolved ions and cannot conduct electricity. Solutions of electrolytes contain ions that permit the passage of electricity. The conductivity of an electrolyte solution is related to the strength of the electrolyte.

Water and other polar molecules are attracted to ions, as shown in Figure \(\PageIndex{2}\), with the negative end of the molecule (oxygen in the case of water) being attracted to cations and the positive end of the molecule (hydrogen in the case of water) being attracted to anions. The electrostatic attraction between an ion and a molecule with a dipole is called an ion–dipole attraction. These attractions play an important role in the dissolution of ionic compounds in water.

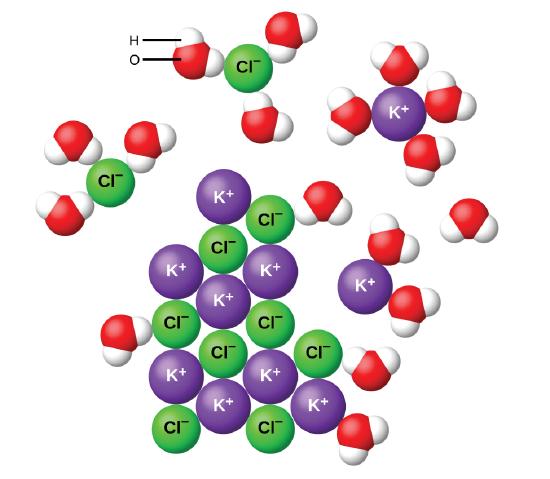
The diagram shows eight purple spheres labeled K superscript plus and eight green spheres labeled Cl superscript minus mixed and touching near the center of the diagram. Outside of this cluster of spheres are seventeen clusters of three spheres, which include one red and two white spheres. A red sphere in one of these clusters is labeled O. A white sphere is labeled H. Two of the green Cl superscript minus spheres are surrounded by three of the red and white clusters, with the red spheres closer to the green spheres than the white spheres. One of the K superscript plus purple spheres is surrounded by four of the red and white clusters. The white spheres of these clusters are closest to the purple spheres. — Figure \(\PageIndex{2}\): As potassium chloride (KCl) dissolves in water, the ions are hydrated. The polar water molecules are attracted by the charges on the K⁺ and Cl⁻ ions. Water molecules in front of and behind the ions are not shown.

When ionic compounds dissolve in water, the ions in the solid separate and disperse uniformly throughout the solution because water molecules surround and solvate the ions, reducing the strong electrostatic forces between them. This process represents a physical change known as dissociation. Under most conditions, many ionic compounds will dissociate nearly completely when dissolved, and so they are classified as strong electrolytes.

✅ Example \(\PageIndex{1}\)

Which compound(s) will dissolve in water to yield ions? (Reminder: Table 7.7.1 and Table 7.7.2 show solubility rules for ionic compounds.)

LiF
P₂F₅
CH₃CH₂OH
MgSO₄

Solution

LiF and MgSO₄will separate into ions when dissolved in water, since they are both ionic compounds. P₂F₅ and CH₃CH₂OH are both molecular compounds and will remain as molecules in a solution.

✏️ Exercise \(\PageIndex{1}\)

Which compound(s) will dissolve in water to yield ions? (Reminder: Table 7.7.1 and Table 7.7.2 show solubility rules for ionic compounds.)

C₆H₁₂O₆ (glucose)
CCl₄
CaCl₂
Cr(NO₃)₃

Answer: CaCl₂ & Cr(NO₃)₃

Ionic compounds are not the only substances that dissolve in water. We previously used the saying "like dissolves like" to describe the fact that polar molecules tend to dissolve in polar solvents and nonpolar molecules tend to dissolve in nonpolar solvents. Because water is a polar molecule, it will tend to dissolve other polar substances. The negative end of the water will be attracted to the positive region of the solute and the positive end of the water will be attracted to the negative region of the solute, creating new dipole–dipole forces between the water and the solute. The interaction will be the most significant when the solute also has hydrogen bonding capabilities with the water. This is why alcohols and sugars which contain hydroxyl (—OH) groups are so soluble in water. Water is often considered to be the "universal solvent" due to the wide variety of ionic, polar, and even some nonpolar compounds that it is able to dissolve.

How Temperature Influences Solubility

The solubility of a substance is the amount of that substance that is required to form a saturated solution in a given amount of solvent at a specified temperature. Solubility is often measured as the grams of solute per 100 g of solvent. The solubility of sodium chloride in water is 36.0 g per 100 g water at 20°C. The temperature must be specified because solubility varies with temperature. For gases, the pressure must also be specified. Solubility is specific for a particular solvent. We will consider the solubility of materials in water as solvent.

The solubility of the majority of solid substances increases as the temperature increases. However, the effect is difficult to predict and varies widely from one solute to another. The temperature dependence of solubility can be visualized with the help of a solubility curve, a graph of the solubility vs. temperature (Figure \(\PageIndex{4}\)).

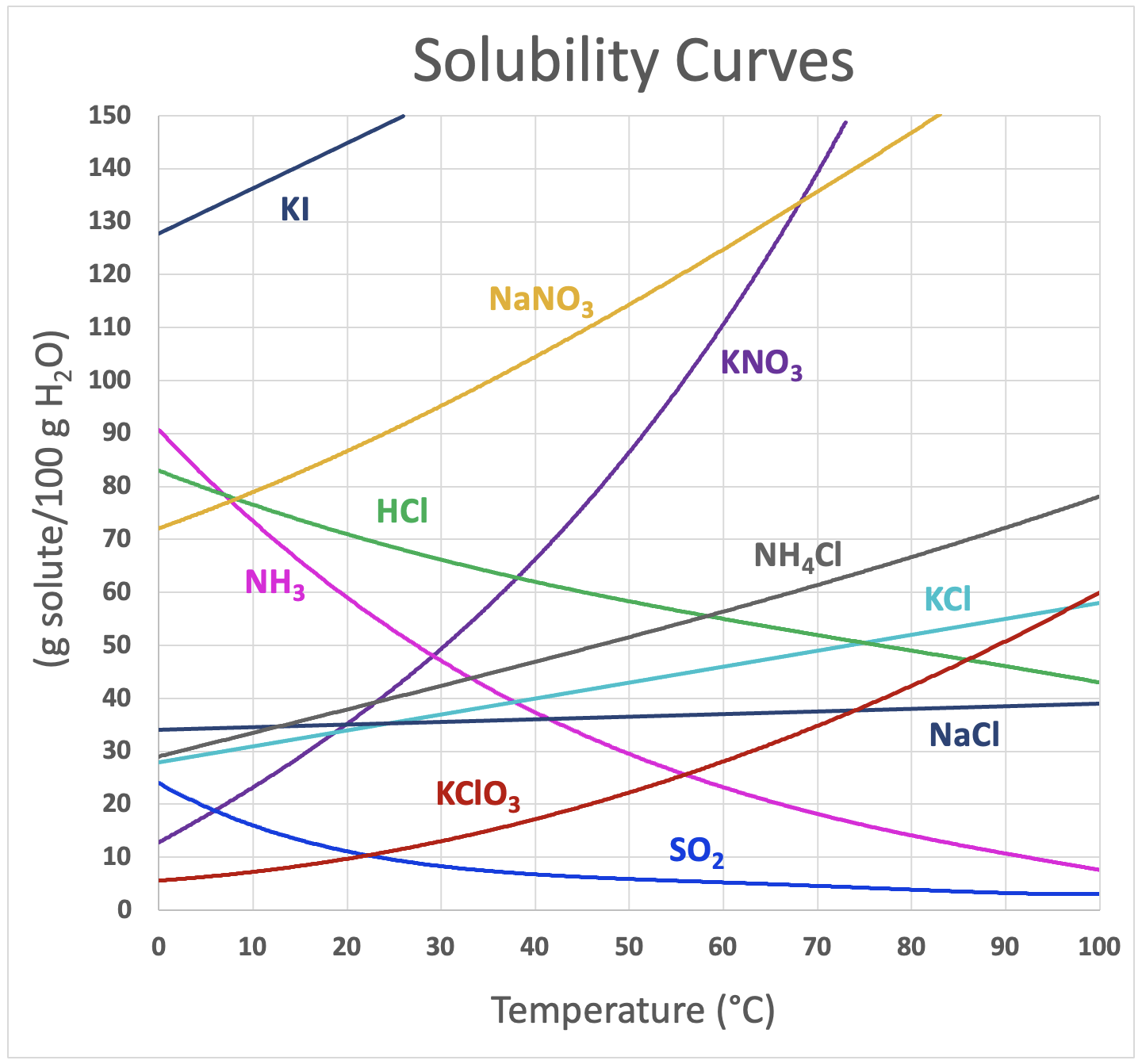
Figure \(\PageIndex{4}\): Solubility curves for several compounds. (adapted from LibreTexts)

Notice how the temperature dependence of NaCl is fairly flat, meaning that an increase in temperature has relatively little effect on the solubility of NaCl. The curve for KNO₃, on the other hand, is very steep and so an increase in temperature dramatically increases the solubility of KNO₃.

Several substances – HCl, NH₃, and SO₂ – have solubility that decreases as temperature increases. They are all gases at standard pressure. When a solvent with a gas dissolved in it is heated, the kinetic energy of both the solvent and solute increase. As the kinetic energy of the gaseous solute increases, its molecules have a greater tendency to escape the attraction of the solvent molecules and return to the gas phase. Therefore, the solubility of a gas decreases as the temperature increases.

Solubility curves can be used to determine if a given solution is saturated or unsaturated. Suppose that 80 g of KNO₃ is added to 100 g of water at 30°C. According to the solubility curve, approximately 49 g of KNO₃ will dissolve at 30°C. This means that the solution will be saturated since 49 g is less than 80 g. We can also determine that there will be 80 g – 49 g = 31 g of undissolved KNO₃remaining at the bottom of the container. Now suppose that this saturated solution is heated to 60°C. According to the curve, the solubility of KNO₃ at 60°C is about 110 g per 100 g of water. Now the solution is unsaturated since it contains only the original 80 g of dissolved solute. Now suppose the solution is cooled all the way down to 0°C. The solubility at 0°C is about 14 g per 100 g of water, meaning that 80 g – 14 g = 66 g of the KNO₃ will recrystallize.

✅ Example \(\PageIndex{2}\)

67 g of each of the following solutes were dissolved in 100 g H₂O at 40°C. Indicate whether the solution is unsaturated, saturated, or supersaturated.

KNO₃
NaNO₃
NH₄Cl

Solution

The graph in Figure \(\PageIndex{4}\) indicates that at 40°C, the solubility of

KNO₃ is 67 g per 100 g H₂O, so the solution would be saturated.
NaNO₃ is 104 g per 100 g H₂O, so the solution would be unsaturated.
NH₄Cl is 48 g per 100 g H₂O, so the solution would be supersaturated.

✏️ Exercise \(\PageIndex{2}\)

How many grams of the indicated solute would dissolve in 100 g H₂O at the given temperature.

SO₂ at 10°C
KClO₃ at 50°C
KI at 20°C

Answer A: 16 g SO₂

Answer B: 22 g KClO₃

Answer C: 146 g KI

✏️ Exercise \(\PageIndex{3}\)

Indicate whether each solution is unsaturated, saturated, or supersaturated. Explain your answer.

15 g NH₃ dissolved in 50 g H₂O at 50°C
50 g NaCl dissolved in 200 g H₂O at 80°C

Answer A: Since the solubility of NH₃ is 30 g per 100 g H₂O at 50°C, half the mass of water (50 g) would dissolve up to 15 g NH₃. Therefore, the solution is saturated.

Answer B: Since the solubility of NaCl is 38 g NH₃ per 100 g H₂O at 80°C, twice the mass of water (200 g) would dissolve up to 76 g NaCl. Therefore, the solution is unsaturated.

Summary

Solubility is the specific amount of solute that can dissolve in a given amount of solvent.
Ionic compounds dissolve in polar solvents, especially water. This occurs when the positive cation from the ionic solid is attracted to the negative end of the water molecule (oxygen) and the negative anion of the ionic solid is attracted to the positive end of the water molecule (hydrogen).
Water is considered the universal solvent since it can dissolve both ionic and polar solutes, as well as some nonpolar solutes (in very limited amounts).
Saturated and unsaturated solutions can be determined using solubility curves.
The solubility of a solid in water increases with an increase in temperature. The solubility of a gas in water decreases with an increase in temperature.

This page is shared under a CK-12 license and was authored, remixed, and/or curated by Melissa Alviar-Agnew, Henry Agnew, Lance S. Lund (Anoka-Ramsey Community College), and Vicki MacMurdo (Anoka-Ramsey Community College).

LICENSED UNDER

Search

Text Color

Text Size

Margin Size

Font Type