10.4: The Bohr Model
- Page ID
- 289416
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)⚙️ Learning Objectives
- Define an energy level in terms of the Bohr model.
- Discuss how the Bohr model can be used to explain atomic spectra.
By 1913, the concept of the atom had evolved from Dalton's indivisible spheres idea, to J. J. Thomson's plum pudding model, and then to Rutherford's nuclear atom theory. Rutherford, in addition to carrying out the brilliant experiment that demonstrated the presence of the atomic nucleus, also proposed that the electrons circled the nucleus in a planetary type motion. The solar system or planetary model of the atom was attractive to scientists because it was similar to something with which they were already familiar, namely the solar system.
Unfortunately, there was a serious flaw in the planetary model. It was already known that when a charged particle (such as an electron) moved in a curved path, it gave off some form of light and loses energy in doing so. This is, after all, how we produce TV signals. If the electron circling the nucleus in an atom loses energy, it would necessarily have to move closer to the nucleus as it loses energy, and would eventually crash into the nucleus. Furthermore, Rutherford's model was unable to describe how electrons give off light forming each element's unique atomic spectrum. These difficulties cast a shadow on the planetary model and indicated that, eventually, it would have to be replaced.
In 1913, the Danish physicist Niels Bohr proposed a model of the electron cloud of an atom in which electrons orbit the nucleus and were able to produce atomic spectra. Understanding Bohr's model requires some knowledge of electromagnetic radiation (or light).
Energy Levels
Bohr's key idea in his model of the atom is that electrons occupy definite orbits that require the electron to have a specific amount of energy. In order for an electron to be in the electron cloud of an atom, it must be in one of the allowable orbitals and it must have the precise energy required for that orbit. Orbits closer to the nucleus would require smaller amounts of energy for an electron, and orbits farther from the nucleus would require the electron to have a greater amount of energy. The possible orbits are known as energy levels. One of the weaknesses of Bohr's model was that he could not offer a reason why only certain energy levels or orbits were allowed.
Bohr hypothesized that the only way electrons could gain or lose energy would be to move from one energy level to another, thus gaining or losing precise amounts of energy. The energy levels are quantized, meaning that only specific amounts are possible. It would be like a ladder that had rungs only at certain heights. The only way you can be on that ladder is to be on one of the rungs, and the only way you could move up or down would be to move to one of the other rungs.
Suppose we had such a ladder with 8 rungs. Other rules for the ladder are that only one person can be on a rung in the normal state, and the ladder occupants must be on the lowest rung available. If the ladder had three people on it, they would be on the lowest three rungs. In this situation, no person could move down because all of the lower rungs are full. Bohr worked out rules for the maximum number of electrons that could be in each energy level in his model, and required that an atom in its normal state (ground state) had all electrons in the lowest energy levels available. Under these circumstances, no electron could lose energy because no electron could move down to a lower energy level. In this way, Bohr's model explained why electrons circling the nucleus did not emit energy and spiral into the nucleus.
Bohr's Model and Atomic Spectra
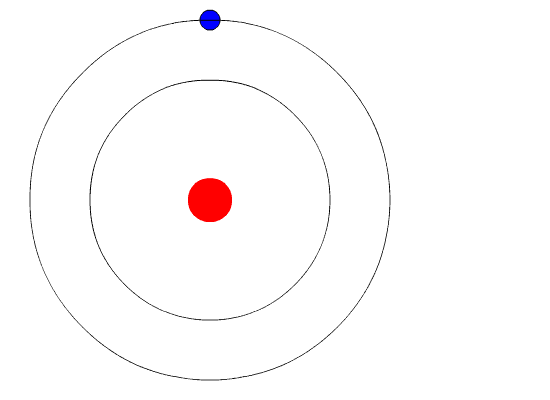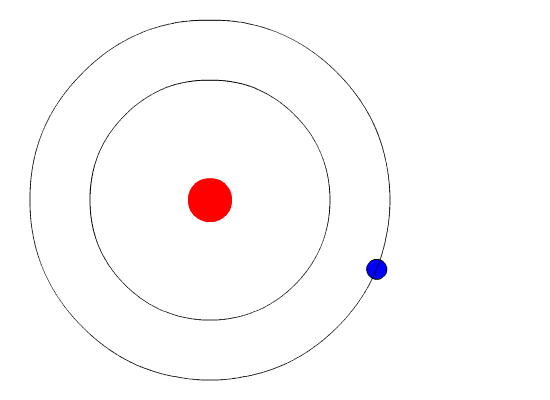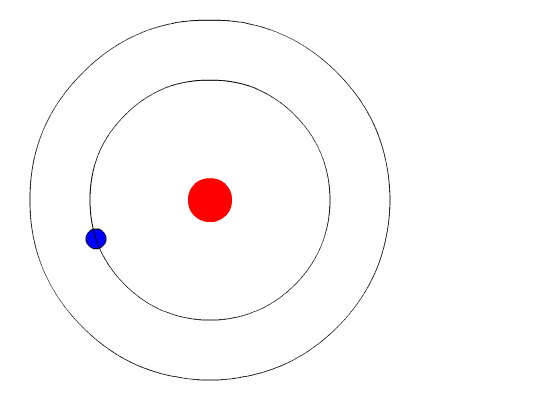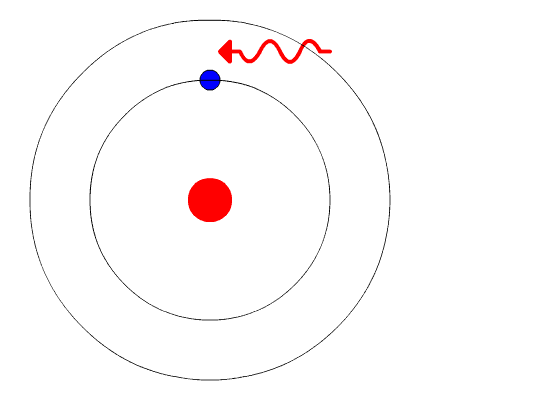
The evidence used to support Bohr's model came from the atomic spectra. He suggested that an atomic spectrum is made by the electrons in an atom changing energy levels. The electrons are typically in their lowest state of potential energy possible, called the ground state (compare it to a ball on the ground in Figure \(\PageIndex{3}\)). If the electrons are provided energy (through heat, electricity, light, etc.), the electrons in an atom could absorb energy by jumping to an energy level with a higher state of potential energy, or excited state (compare it to a ball at the platform level near the top in Figure \(\PageIndex{3}\)). The electrons then give off the energy in the form of a piece of light – called a photon – that they had absorbed, to fall back to a lower energy level. The energy emitted by electrons dropping back to lower energy levels will always be precise amounts of energy, because the differences in energy levels are precise.

This explains why you see specific lines of light when looking at an atomic spectrum – each line of light matches a specific "step down" that an electron can take in that atom. This also explains why each element produces a different atomic spectrum. Because each element has different acceptable energy levels for its electrons, the possible steps each element's electrons can take differ from all other elements. In the case of hydrogen's emission spectrum, the wavelengths in the visible portion of the spectrum all involve transitions where an electron drops from a higher energy level down to the second energy level (n = 2). See Figure \(\PageIndex{4}\).
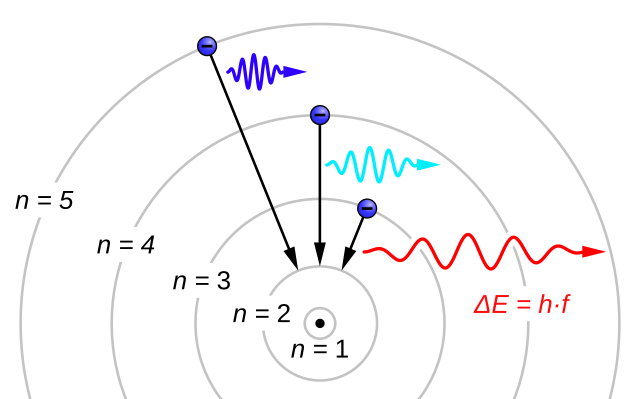
As an interesting side note, these jumps between quantized energy levels are called quantum jumps or quantum leaps. Since the electron had to undergo an immediate transition from one energy level to another instantaneously, in effect, the electron could not exist in between. This expression took on a new meaning to represent huge leaps or advancements in knowledge, power, or technology. In science fiction, a quantum leap is typically thought of as being a huge jump across space and or time, as was popularized in the TV show, Quantum Leap.
Summary
- Bohr's model suggests each atom has a set of unchangeable energy levels, and electrons in the electron cloud of that atom must be in one of those energy levels.
- Bohr's model suggests that the atomic spectra of atoms is produced by electrons gaining energy from some source, jumping up to a higher energy level, then immediately dropping back to a lower energy level and emitting the energy difference between the two energy levels.
- The existence of the atomic spectra is support for Bohr's model of the atom.
This page is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by Marisa Alviar-Agnew, Lance S. Lund (Anoka-Ramsey Community College), and Henry Agnew.

