10.5: Quantum Mechanics and Atomic Orbitals
- Page ID
- 289417
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)⚙️ Learning Objectives
- Define quantum mechanics.
- Differentiate between an orbit and an orbital.
How do you study something that seemingly makes no sense? We talk about electrons being in orbits and it sounds like we can tell where that electron is at any moment. We can draw pictures of electrons in orbit, but the reality is that we don't know exactly where they are. We are going to take a look at an area of science that even leaves scientists puzzled. When asked about quantum mechanics, Niels Bohr (who proposed the Bohr model of the atom) said: "Anyone who is not shocked by quantum theory has not understood it." Richard Feynman (one of the founders of modern quantum theory) stated: "I think I can safely say that nobody understands quantum theory." So, let's take a short trip into a land that challenges our everyday world.
Quantum Mechanics
The study of motion of large objects such as baseballs is called mechanics, or more specifically, classical mechanics. When a baseball is thrown, we can predict the exact path of the baseball at any point in time based on its velocity and the angle at which it is thrown. Because of the quantum nature of the electron and other tiny particles moving at high speeds, classical mechanics is inadequate to accurately describe their motion. Quantum mechanics is the study of the motion of objects that are atomic or subatomic in size and thus demonstrate wave-particle duality. In classical mechanics, the size and mass of the objects involved effectively obscures any quantum effects, so that such objects appear to gain or lose energies in any amounts. Particles whose motion is described by quantum mechanics gain or lose energy in small pieces called quanta.
One of the fundamental (and hardest to understand) principles of quantum mechanics is that the electron is both a particle and a wave. In the everyday macroscopic world of things we can see, something cannot be both. However, this duality exists in the quantum world of the submicroscopic on the atomic scale. At the heart of quantum mechanics is the idea that we cannot accurately specify the location of an electron. If we learn something about its location, we know less about its speed. If we learn something about its speed, we know less about its location. This observation became known as the Heisenberg uncertainty principle in recognition of the mathematical observation by Werner Heisenberg in 1927. All we can say is that there is a probability that it exists within a certain volume of space.
The scientist, Erwin Schrödinger, developed an equation that deals with these calculations, often referred to as the Schrödinger wave equation, in which electrons were treated as if they were waves. The wave equation defined orbitals to depict the locations of electrons in atoms to replace the circular orbits that were central to the Bohr model. These orbitals were defined as regions of space where there is a high probability of finding an electron.
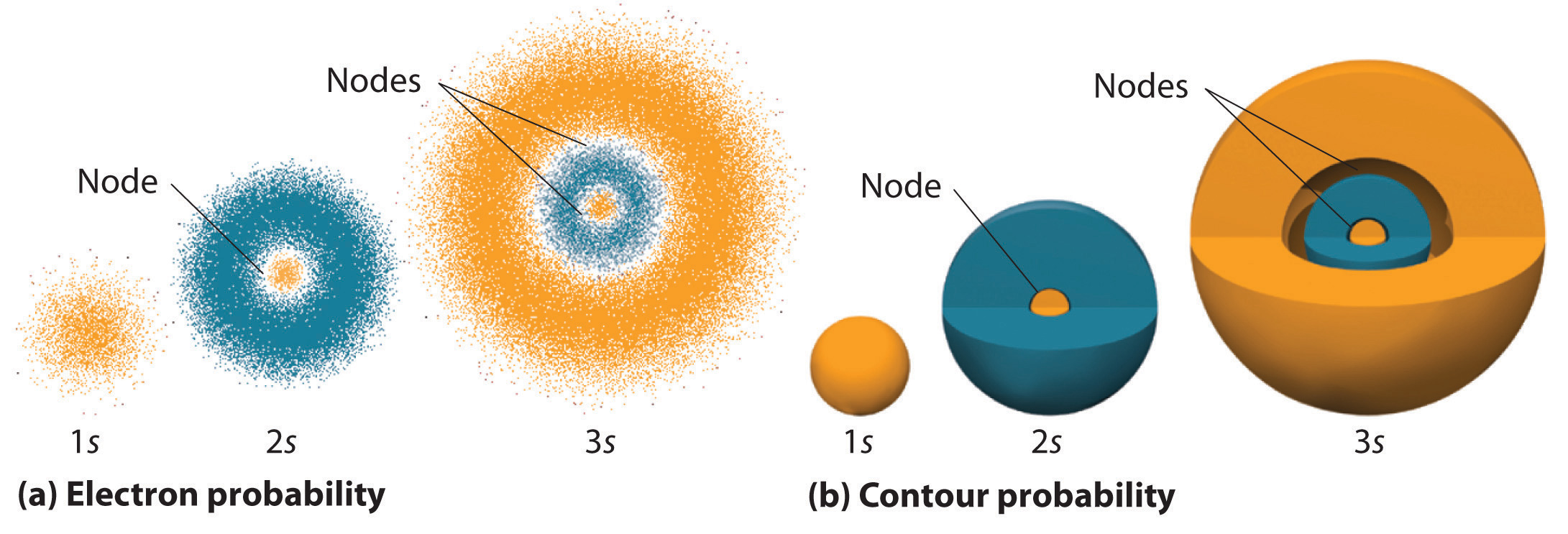
When looking at the orbital depictions in Figure \(\PageIndex{1(a)}\), areas where the dots are more densely shaded represent areas where finding an electron is more probable. By drawing the probabilities as contours in Figure \(\PageIndex{1(b)}\), it is easy to see that the orbitals become progressively larger as one moves to higher energy levels (shown by the numbers 1, 2, and 3). This is similar to how each orbit in the Bohr model becomes progressively farther from the nucleus. In other words, the larger the orbital, the greater the relative energy of the electron.

As one moves to higher energy levels, each energy level has a greater number of possible orbitals. In addition to a greater number of possible orbitals, the types of available orbitals become increasingly complex (see Figure \(\PageIndex{2}\)). The increasing complexity of these orbitals is analogous to the increased vibrational frequency of a guitar string as the string is stretched (see Figure \(\PageIndex{3}\)). The vibrational frequency increases as the number of nodes (or standing waves) increases. As described in Section 10.1, energy and frequency are directly proportional. This means that as the frequency increases, so does the energy. In the case of orbitals, as the complexity of an orbital increases, so does its energy. Therefore, electrons in the same energy level that reside in orbitals that are more complex have a greater energy than those that reside in orbitals that are less complex. In other words, the greater the complexity of the orbitals, the greater the relative energy of the electron.

What does all of this mean? In the Bohr model, electrons had to jump from one orbit to another when they they absorbed or released energy on an instantaneous basis; they could not exist anywhere between the orbits. The modern model, called the quantum mechanical model, overcomes this issue.
In the quantum mechanical model, electrons transition from orbitals of lesser energy to ones with greater energy (either larger and/or more complex orbitals) when they absorb energy, while they transition from orbitals of greater energy to ones with lesser energy (either smaller and/or less complex orbitals) when they release energy. Since orbitals are defined based on probabilities of finding an electron in spaces that overlap each other in three-dimensional space rather than very specific, non-overlapping orbits in the Bohr model, the jumps between quantized energy levels and/or orbitals are much more easily explained.
The energy of an electron in an atom depends on the ____ and ____ of the orbital in which it resides.
- size
- wave
- shape
- particle
- nucleus
Solution
The energy of an electron in an atom depends on the (A) size and (C) shape of the orbital in which it resides.
✏️ Exercise \(\PageIndex{1}\)
- An electron in an orbital has the most energy if the size of the orbital is
- larger
- smaller
- medium-sized
- orbital size has nothing to do with the energy of the electron.
- An electron in an orbital has the most energy if the shape of the orbital is
- complex.
- simple.
- orbital shape has nothing to do with the energy of the electron.
- Answer A
- 1. larger
- Answer B
- 1. complex
Summary
- Quantum mechanics involves the study of material at the atomic level. This field deals with probabilities, since we cannot definitely locate a particle.
- Orbitals are mathematically derived regions of space with different probabilities of having an electron.
This page is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Lance S. Lund (Anoka-Ramsey Community College), Marisa Alviar-Agnew, and Henry Agnew.

