1.3: Photoelectric Effect Explained with Quantum Hypothesis
- Page ID
- 13383
- To be familiar with the photoelectron effect for bulk materials
- Understand how the photoelectron kinetic energy and intensity vary as a function of incident light wavelength
- Understand how the photoelectron kinetic energy and intensity vary as a function of incident light intensity
- Describe what a workfunction is and relate it to ionization energy
- Describe the photoelectric effect with Einstein's quantized photon model of light
Nature, it seemed, was quantized (non-continuous, or discrete). If this was so, how could Maxwell’s equations correctly predict the result of the blackbody radiator? Planck spent a good deal of time attempting to reconcile the behavior of electromagnetic waves with the discrete nature of the blackbody radiation, to no avail. It was not until 1905, with yet another paper published by Albert Einstein, that the wave nature of light was expanded to include the particle interpretation of light which adequately explained Planck’s equation.
The photoelectric effect was first documented in 1887 by the German physicist Heinrich Hertz and is therefore sometimes referred to as the Hertz effect. While working with a spark-gap transmitter (a primitive radio-broadcasting device), Hertz discovered that upon absorption of certain frequencies of light, substances would give off a visible spark. In 1899, this spark was identified as light-excited electrons (called photoelectrons) leaving the metal's surface by J.J. Thomson (Figure 1.3.1 ).
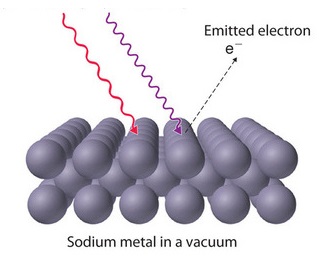
The classical picture underlying the photoelectron effect was that the atoms in the metal contained electrons, that were shaken and caused to vibrate by the oscillating electric field of the incident radiation. Eventually some of them would be shaken loose, and would be ejected from the cathode. It is worthwhile considering carefully how the number and speed of electrons emitted would be expected to vary with the intensity and color of the incident radiation along with the time needed to observe the photoelectrons.
- Increasing the intensity of radiation would shake the electrons more violently, so one would expect more to be emitted, and they would shoot out at greater speed, on average.
- Increasing the frequency of the radiation would shake the electrons faster, so it might cause the electrons to come out faster. For very dim light, it would take some time for an electron to work up to a sufficient amplitude of vibration to shake loose.
Lenard's Experimental Results (Intensity Dependence)
In 1902, Hertz's student, Philipp Lenard, studied how the energy of the emitted photoelectrons varied with the intensity of the light. He used a carbon arc light and could increase the intensity a thousand-fold. The ejected electrons hit another metal plate, the collector, which was connected to the cathode by a wire with a sensitive ammeter, to measure the current produced by the illumination (Figure 1.3.2 ). To measure the energy of the ejected electrons, Lenard charged the collector plate negatively, to repel the electrons coming towards it. Thus, only electrons ejected with enough kinetic energy to get up this potential hill would contribute to the current.
Lenard discovered that there was a well defined minimum voltage that stopped any electrons getting through (\(V_{stop}\)). To Lenard's surprise, he found that \(V_{stop}\) did not depend at all on the intensity of the light! Doubling the light intensity doubled the number of electrons emitted, but did not affect the kinetic energies of the emitted electrons. The more powerful oscillating field ejected more electrons, but the maximum individual energy of the ejected electrons was the same as for the weaker field (Figure 1.3.2 ).
Millikan's Experimental Results (Wavelength Dependence)
The American experimental physicist Robert Millikan followed up on Lenard's experiments and using a powerful arc lamp, he was able to generate sufficient light intensity to separate out the colors and check the photoelectric effect using light of different colors. He found that the maximum energy of the ejected electrons did depend on the color - the shorter wavelength, higher frequency light eject photoelectrons with greater kinetic energy (Figures 1.3.3 ).
As shown in Figure 1.3.4 , just the opposite behavior from classical is observed from Lenard's and Millikan's experiments. The intensity affects the number of electrons, and the frequency affects the kinetic energy of the emitted electrons. From these sketches, we see that
- the kinetic energy of the electrons is linearly proportional to the frequency of the incident radiation above a threshold value of \(ν_0\) (no current is observed below \(ν_0\)), and the kinetic energy is independent of the intensity of the radiation, and
- the number of electrons (i.e. the electric current) is proportional to the intensity and independent of the frequency of the incident radiation above the threshold value of \(ν_0\) (i.e., no current is observed below \(ν_0\)).
Classical theory predicts that energy carried by light is proportional to its amplitude independent of its frequency, and this fails to correctly explain the observed wavelength dependence in Lenard's and Millikan's observations.
As with most of the experimental results we discuss in this text, the behavior described above is a simplification of the true experimental results observed in the laboratory. A more complex description involves a greater introduction of more complex physics and instrumentation, which will be ignored for now.
Einstein's Quantum Picture
In 1905 Einstein gave a very simple interpretation of Lenard's results and borrowed Planck's hypothesis about the quantized energy from his blackbody research and assumed that the incoming radiation should be thought of as quanta of energy \(h\nu\), with \(\nu\) the frequency. In photoemission, one such quantum is absorbed by one electron. If the electron is some distance into the material of the cathode, some energy will be lost as it moves towards the surface. There will always be some electrostatic cost as the electron leaves the surface, which is the workfunction, \(\Phi\). The most energetic electrons emitted will be those very close to the surface, and they will leave the cathode with kinetic energy
\[KE = h\nu - \Phi \label{Eq1} \]
On cranking up the negative voltage on the collector plate until the current just stops, that is, to \(V_{stop}\), the highest kinetic energy electrons (\(KE_e\)) must have had energy \(eV_{stop}\) upon leaving the cathode. Thus,
\[eV_{stop} = h\nu - \Phi \label{Eq2} \]
Thus, Einstein's theory makes a very definite quantitative prediction: if the frequency of the incident light is varied, and \(V_{stop}\) plotted as a function of frequency, the slope of the line should be \(\frac{h}{e}\) (Figure \(\PageIndex{4A}\)). It is also clear that there is a minimum light frequency for a given metal \(\nu_o\), that for which the quantum of energy is equal to \(\Phi\) (Equation \ref{Eq1}). Light below that frequency, no matter how bright, will not eject electrons.
According to both Planck and Einstein, the energy of light is proportional to its frequency rather than its amplitude, there will be a minimum frequency \(\nu_0\) needed to eject an electron with no residual energy.
Since every photon of sufficient energy excites only one electron, increasing the light's intensity (i.e. the number of photons/sec) only increases the number of released electrons and not their kinetic energy. In addition, no time is necessary for the atom to be heated to a critical temperature and therefore the release of the electron is nearly instantaneous upon absorption of the light. Finally, because the photons must be above a certain energy to satisfy the workfunction, a threshold frequency exists below which no photoelectrons are observed. This frequency is measured in units of Hertz (1/second) in honor of the discoverer of the photoelectric effect.
Einstein's Equation \(\ref{Eq1}\) explains the properties of the photoelectric effect quantitatively. A strange implication of this experiment is that light can behave as a kind of massless "particle" now known as a photon whose energy \(E=h\nu\) can be transferred to an actual particle (an electron), imparting kinetic energy to it, just as in an elastic collision between to massive particles such as billiard balls.
Robert Millikan initially did not accept Einstein's theory, which he saw as an attack on the wave theory of light, and worked for ten years until 1916, on the photoelectric effect. He even devised techniques for scraping clean the metal surfaces inside the vacuum tube. For all his efforts he found disappointing results: he confirmed Einstein's theory after ten years. In what he writes in his paper, Millikan is still desperately struggling to avoid this conclusion. However, by the time of his Nobel Prize acceptance speech, he has changed his mind rather drastically!
Einstein's simple explanation (Equation \ref{Eq1}) completely accounted for the observed phenomena in Lenard's and Millikan's experiments (Figure 1.3.4 ) and began an investigation into the field we now call quantum mechanics. This new field seeks to provide a quantum explanation for classical mechanics and create a more unified theory of physics and thermodynamics. The study of the photoelectric effect has also lead to the creation of new field of photoelectron spectroscopy. Einstein's theory of the photoelectron presented a completely different way to measure Planck's constant than from black-body radiation.
The Workfunction (Φ)
The workfunction is an intrinsic property of the metal. While the workfunctions and ionization energies appear as similar concepts, they are independent. The workfunction of a metal is the minimum amount of energy (\(\ce{E}\)) necessary to remove an electron from the surface of the bulk (solid) metal (sometimes referred to as binding energy).
\[\ce{M (s) + \Phi \rightarrow M^{+}(s) + e^{-}}(\text{free with no kinetic energy}) \nonumber \]
The workfunction is qualitatively similar to ionization energy (\(\ce{IE}\)), which is the amount of energy required to remove an electron from an atom or molecule in the gaseous state.
\[\ce{M (g) + IE \rightarrow M^{+}(g) + e^{-}} (\text{free with no kinetic energy}) \nonumber \]
However, these two energies differ in magnitude (Table 1.3.1 ). For instance, copper has a workfunction of about 4.7 eV, but has a higher ionization energy of 7.7 eV. Generally, the ionization energies for metals are greater than the corresponding workfunctions (i.e., the electrons are less tightly bound in bulk metal).
| Element | Workfunction \(\Phi\) (eV) | Ionization Energy (eV) |
|---|---|---|
| Lithium (Li) | 2.93 | 5.39 |
| Beryllium (Be) | 4.98 | 9.32 |
| Boron (B) | 4.45 | 8.298 |
| Carbon (C) | 5.0 | 11.26 |
| Sodium (Na) | 2.36 | 5.13 |
| Aluminum (Al) | 4.20 | 5.98 |
| Silicon (Si) | 4.85 | 8.15 |
| Potassium (K) | 2.3 | 4.34 |
| Iron (Fe) | 4.67 | 7.87 |
| Cobalt (Co) | 4.89 | 7.88 |
| Copper (Cu) | 4.7 | 7.7 |
| Gallium (Ga) | 4.32 | 5.99 |
| Germanium (Ge) | 5.0 | 7.89 |
| Arsenic (As) | 3.75 | 9.81 |
| Selenium (Se) | 5.9 | 9.75 |
| Silver (Ag) | 4.72 | 7.57 |
| Tin (Sn) | 4.42 | 7.34 |
| Cesium (Cs) | 1.95 | 3.89 |
| Gold (Au) | 5.17 | 9.22 |
| Mercury (Hg)liquid | 4.47 | 10.43 |
| Bismuth (Bi) | 4.34 | 7.29 |
- What is the energy in joules and electron volts of a photon of 420-nm violet light?
- What is the maximum kinetic energy of electrons ejected from calcium by 420-nm violet light, given that the workfunction for calcium metal is 2.71 eV?
Strategy
To solve part (a), note that the energy of a photon is given by \(E=h\nu\). For part (b), once the energy of the photon is calculated, it is a straightforward application of Equation \ref{Eq1} to find the ejected electron’s maximum kinetic energy, since \(\Phi\) is given.
Solution for (a)
Photon energy is given by
\[E = h\nu \nonumber \]
Since we are given the wavelength rather than the frequency, we solve the familiar relationship \(c=\nu\lambda\) for the frequency, yielding
\[\nu=\dfrac{c}{\lambda} \nonumber \]
Combining these two equations gives the useful relationship
\[E=\dfrac{hc}{\lambda} \nonumber \]
Now substituting known values yields
\[\begin{align*} E &= \dfrac{(6.63 \times 10^{-34}\; J \cdot s)(3.00 \times 10^8 m/s)}{420 \times 10^{-9}\; m} \\[4pt] &= 4.74 \times 10^{-19}\; J \end{align*} \nonumber \]
Converting to eV, the energy of the photon is
\[\begin{align*} E&=(4.74 \times 10^{-19}\; J) \left( \dfrac{1 \;eV}{1.6 \times 10^{-19}\;J} \right) \\[4pt] &= 2.96\; eV. \nonumber \end{align*} \nonumber \]
Solution for (b)
Finding the kinetic energy of the ejected electron is now a simple application of Equation \ref{Eq1}. Substituting the photon energy and binding energy yields
\[\begin{align*} KE_e &=h\nu – \Phi \\[4pt] &= 2.96 \;eV – 2.71 \;eV \\[4pt] &= 0.246\; eV.\nonumber \end{align*} \nonumber \]
Discussion
The energy of this 420-nm photon of violet light is a tiny fraction of a joule, and so it is no wonder that a single photon would be difficult for us to sense directly—humans are more attuned to energies on the order of joules. But looking at the energy in electron volts, we can see that this photon has enough energy to affect atoms and molecules. A DNA molecule can be broken with about 1 eV of energy, for example, and typical atomic and molecular energies are on the order of eV, so that the UV photon in this example could have biological effects.
The ejected electron (called a photoelectron) has a rather low energy, and it would not travel far, except in a vacuum. The electron would be stopped by a retarding potential of 0.26 eV. In fact, if the photon wavelength were longer and its energy less than 2.71 eV, then the formula would give a negative kinetic energy, an impossibility. This simply means that the 420-nm photons with their 2.96-eV energy are not much above the frequency threshold. You can show for yourself that the threshold wavelength is 459 nm (blue light). This means that if calcium metal is used in a light meter, the meter will be insensitive to wavelengths longer than those of blue light. Such a light meter would be insensitive to red light, for example.
What is the longest-wavelength electromagnetic radiation that can eject a photoelectron from silver? Is this in the visible range?
- Answer
-
Given that the workfunction is 4.72 eV from Table 1.3.1 , then only photons with wavelengths lower than 263 nm will induce photoelectrons (calculated via \(E=h \nu\)). This is ultraviolet and not in the visible range.
Why is the workfunction of an element generally lower than the ionization energy of that element?
- Answer
-
The workfunction of a metal refers to the minimum energy required to extract an electron from the surface of a (bulk) metal by the absorption a photon of light. The workfunction will vary from metal to metal. In contrast, ionization energy is the energy needed to detach electrons from atoms and also varies with each particular atom, with the valence electrons require less energy to extract than core electrons (i.e., from lower shells) that are more closely bound to the nuclei. The electrons in the metal lattice there less bound (i.e., free to move within the metal) and removing one of these electrons is much easier than removing an electron from an atom because the metallic bonds of the bulk metal reduces their binding energy. As we will show in subsequent chapters, the more delocalized a particle is, the lower its energy.
Summary
Although Hertz discovered the photoelectron in 1887, it was not until 1905 that a theory was proposed that explained the effect completely. The theory was proposed by Einstein and it made the claim that electromagnetic radiation had to be thought of as a series of particles, called photons, which collide with the electrons on the surface and emit them. This theory ran contrary to the belief that electromagnetic radiation was a wave and thus it was not recognized as correct until 1916 when Robert Millikan experimentally confirmed the theory
The photoelectric effect is the process in which electromagnetic radiation ejects electrons from a material. Einstein proposed photons to be quanta of electromagnetic radiation having energy \(E=h\nu\) is the frequency of the radiation. All electromagnetic radiation is composed of photons. As Einstein explained, all characteristics of the photoelectric effect are due to the interaction of individual photons with individual electrons. The maximum kinetic energy \(KE_e\) of ejected electrons (photoelectrons) is given by \(KE_e=h\nu – \Phi\), where \(h\nu\) is the photon energy and \(\Phi\) is the workfunction (or binding energy) of the electron to the particular material.
Conceptual Questions
- Is visible light the only type of electromagnetic radiation that can cause the photoelectric effect?
- Which aspects of the photoelectric effect cannot be explained without photons? Which can be explained without photons? Are the latter inconsistent with the existence of photons?
- Is the photoelectric effect a direct consequence of the wave character of electromagnetic radiation or of the particle character of electromagnetic radiation? Explain briefly.
- Insulators (nonmetals) have a higher \(\Phi\) than metals, and it is more difficult for photons to eject electrons from insulators. Discuss how this relates to the free charges in metals that make them good conductors.
- If you pick up and shake a piece of metal that has electrons in it free to move as a current, no electrons fall out. Yet if you heat the metal, electrons can be boiled off. Explain both of these facts as they relate to the amount and distribution of energy involved with shaking the object as compared with heating it.
Contributors and Attributions
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski ("Quantum States of Atoms and Molecules")
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).

