Hydration
- Page ID
- 37387
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- What is the energy of hydration?
- How is hydration energy related to lattice energy?
- What is enthalpy of solvation?
The formation of a solution involves the interaction of solute with solvent molecules. Many different liquids can be used as solvents for liquid solutions, and water is the most commonly used solvent. When water is used as the solvent, the dissolving process is called hydration. The interaction between water molecules and sodium ion is illustrated as one of the diagram below. This is a typical ion-dipole interaction. At the molecular level, the ions interact with water molecules from all directions in a 3-dimensional space. This diagram depicts the concept of interaction only.

The above diagram also display hydrogen-bonding, dipole-dipole, ion-induced dipole, and dipole-induced dipole interactions. In the absence of these interactions, solvation takes place due to dispersion. Definitions of these terms are obvious from the diagrams. The meaning of the words used in the term also hints the nature of the interactions.
What is the Enthalpy of Hydration?
Enthalpy of hydration, \(\Delta H_{hyd}\), of an ion is the amount of heat released when a mole of the ion dissolves in a large amount of water forming an infinite dilute solution in the process,
\[M^{z+}_{(g)} + mH_2O \rightarrow M^{z+}_{(aq)} \label{1}\]
where Mz+(aq) represents ions surrounded by water molecules and dispersed in the solution. The approximate hydration energies of some typical ions are listed here. Figure \(\PageIndex{1}\) illustrates the point that as the atomic numbers increases, so do the ionic size, leading to a decrease in absolute values of enthalpy of hydration.
| Ion | \(\Delta H_{hyd}\) | Ion | \(\Delta H_{hyd}\) | Ion | \(\Delta H_{hyd}\) |
|---|---|---|---|---|---|
| H+ | -1130 | Al3+ | -4665 | Fe3+ | -4430 |
| -- | |||||
| Li+ | -520 | Be2+ | -2494 | F- | -505 |
| Na+ | -406 | Mg2+ | -1921 | Cl- | -363 |
| K+ | -322 | Ca2+ | -1577 | Br- | -336 |
| Rb+ | -297 | Sr2+ | -1443 | I- | -295 |
| Cs+ | -276 | Ba2+ | -1305 | ClO4- | -238 |
| -- | |||||
| Cr2+ | -1904 | Mn2+ | -1841 | Fe2+ | -1946 |
| Co2+ | -1996 | Ni2+ | -2105 | Cu2+ | -2100 |
| Zn2+ | -2046 | Cd2+ | -1807 | Hg2+ | -1824 |
From the above table, an estimate can be made for the hydration energy of sodium chloride. The hydration energy of an ionic compound consists of two inseparable parts. The first part is the energy released when the solvent forms a coordination compound with the ions. This energy released is called the Enthalpy of ligation, \(\Delta H_{lig}\). The processes related to these energies are shown below:
\[M^{z+} + nL \rightarrow ML_n^{z+} \;\;\; \Delta H_{lig} \label{2}\]
\[ML_n^{z+} + solvent \rightarrow ML^{z+}_{n(sol)} \;\;\; \Delta H_{disp} \label{3}\]
The second step is to disperse the ions or hydrated ions into the solvent medium, which has a dielectric constant different from vacuum. This amount of energy is called energy of dispersion, \(\Delta H_{disp}\). Therefore,
\[\Delta H_{hyd} = \Delta H_{disp} + \Delta H_{lig} \label{4}\]
This idea is brought up just to point out that the formation of aqua complex ions is part of the hydration process, even though the two energies are not separable. When stronger coordination is made between the ions and other ligands, they replace the coordinated water molecules if they are present. In the presence of NH3 molecules, they replace the water of Cu(H2O)62+:
\[Cu(H_2O)_6^{2+} + 6NH_3 \rightarrow Cu(NH_3)_6^{2+} + 6H_2O \label{5}\]
Relating Hydration Energy to Lattice Enthalpy
In the discussion of lattice energy, we consider the ions separated into a gas form whereas in the dissolution process, the ions are also separated, but this time into ions dispersed in a medium with solvent molecules between ions. The medium or solvent has a dielectric constant. The molar enthalpy of solution, \(\Delta H_{sol}\), is the energy released when one mole solid is dissolved in a solvent. This quantity, the enthalpy of crystallization, and energy of hydration forms a cycle. Taking the salt \(\ce{NaCl}\) as an example, the following relationship is obvious,
\[\Delta H_{sol} =\Delta H_{lattice} + \Delta H_{hydration} \label{4A}\]
from the following diagram.
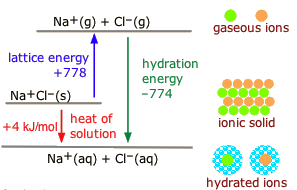
The term enthalpy of crystallization is used in this diagram instead of lattice energy so that all the arrows point downward. Note that enthalpy of crystallization \(H_{cryst}\), and energy of crystallization, \(E_{cryst}\) refer to the same quantity, and they are used interchangably. The enthalpies of solution for some salts can be positive values, in these cases the temperatures of the solution decrease as the substances dissolve; the dissolving is an endothermic reaction. The energy levels of solids and solutions reverse in order of height.
What is Enthalpy of Solution?
The molar enthalpy of solution, \(\Delta H_\ce{sol}\), is the energy released when one mole of solid is dissolved in a solvent.
Sometimes the enthalpy of hydration is also (mis)understood as \(\Delta H_\ce{sol}\). When apply these values, make sure you understand the process involved.
| Substance | \(\Delta H_{sol}\) | Substance | \(\Delta H_{sol}\) |
|---|---|---|---|
| AlCl3(s) | -373.63 | H2SO4(l) | -95.28 |
| LiNO3(s) | -2.51 | LiCl(s) | -37.03 |
| NaNO3(s) | 20.50 | NaCl(s) | 3.88 |
| KNO3(s) | 34.89 | KCl(s) | -17.22 |
| NaOH(s) | -44.51 | NH4Cl(s) | 14.77 |
These values indicates that when aluminum chloride and sulfuric acid are dissolved in water, much heat is released. Due to the very small value of enthalpies of solution, the temperature changes are hardly noticed when LiNO3 and NaCl are dissolving.
The lattice energy of NaCl calculated using the Madelung constant of the NaCl structure type is +788 kJ/mol. The estimated enthalpy of hydration for sodium and chloride ions are -406 and -363 kJ/mol respectively. Estimate the enthalpy of solvation for NaCl.
Solution
Using the cycle in Figure \(\PageIndex{2}\) and Equation \ref{4A}, we have
\[\Delta H_{hyd} = \Delta H_{lattice} + \Delta H_{sol} \nonumber\]
\[\Delta H_{sol} = -769 - (788)\; kJ = -19\, kJ/mol \nonumber\]
DISCUSSION
A positive value indicates an endothermic reaction. However, the value is small, and depending on the source of data, the estimated value may change. This value of 19 kJ/mol is too high compared to the value given earlier for NaCl of 3.88 kJ/mol, due to a high value of lattice energy used.
The enthalpy of crystallization for KCl is -715 kJ/mol. The enthalpies of hydration for potassium and chloride are -322 and -363 kJ/mol respectively. From these values, estimate the enthalpy of solution for KCl.
Solution
The enthalpy of hydration for KCl is estimated to be
\[\Delta H_{hyd}= -322 + (-363) = -685 kJ/mol \nonumber\]
Thus, the enthalpy of solution is
\[\Delta H_{sol}= -685 - (-715) = 30 kJ/mol \nonumber\]
DISCUSSION
The enthalpy of solution given above is -17.22. The two values here indicates that dissolving \(\ce{KCl}\) into water is an endothermic reaction or change. Should temperature decrease or increase when \(\ce{KCl}\) dissolves?
Questions
- What types of interaction are present when CaCl2 dissolves in ethanol?
- What is the major type of interaction when toluene dissolves in benzene?
- Which ion has a larger absolute value of enthalpy of hydration, Na+ or Ca2+?
- Which ion is larger, Na+ or Cl-?
- When KNO3 is dissolving in water, will the temperature decrease or increase?
Solutions
- Skill -
Identify the type of interactions in the solvation process. - Discussion -
Toluene and benzene form ideal solution in that total vapor pressure of the solution is the sum of the partial pressures of benzene and toluene. These two compounds are so much a like that their molecules disperse into each other. The major driving force for solution is entropy. - Skill -
The ion-dipole interaction is stronger between Ca2+ and water molecules than between Na+ and water molecules. - Discussion -
What are their electronic configuration? The sodium ion has the same electronic configuration as Ne, but the chloride ion has the same electronic configuration as Ar, which is larger than Ne. Which one release more energy when hydrated? - Discussion -
Among the substances listed in the table above, KNO3 absorbed the most energy per mole when dissolved.
Contributors and Attributions
Chung (Peter) Chieh (Professor Emeritus, Chemistry @ University of Waterloo)


