Isotope Effects in Vibrational Spectroscopy
- Page ID
- 1854
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page provides an overview of how an isotope can affect the frequencies of the vibrational modes of a molecule. Isotopic substitution is a useful technique due to the fact that the normal modes of an isotopically substituted molecule are different than the normal modes of an unsubstituted molecule, leading to different corresponding vibrational frequencies for the substituted atoms. Vibrational spectroscopy is done in the infrared region of the electromagnetic spectrum, which ranges from around 10-6 to 10-3 meters. IR and Raman spectroscopy observe the vibrations of molecules, displaying the normal and local modes of the molecule in the spectra. Isotopes are atoms that share the same number of protons but differ in the number of neutrons contained in the nucleus, thus giving these atoms different mass numbers. The specific mass of each atom will affect the reduced mass of the overall molecule, therefore changing the vibrational frequencies of that molecule.
Diatomics
A diatomic molecule, as seen in Figure \(\PageIndex{1}\), contains two atoms, which can either be composed of the same or different elements. It is easier to focus on these types of molecules when analyzing and calculating vibrational frequencies because they are simpler systems than polyatomic molecules. Whether or not the diatomic consists of the same or different elements, a diatomic molecule will have only one vibrational frequency. This singular normal mode is because of the diatomic's linear symmetry, so the only vibration possible occurs along the bond connecting the two atoms.
Normal Modes
Normal modes describe the possible movements/vibrations of each of the atoms in a system. There are many different types of vibrations that molecules can undergo, like stretching, bending, wagging, rocking, and twisting, and these types can either be out of plane, asymmetric, symmetric, or degenerate. Molecules have 3n possible movements due to their 3-dimensionality, where n is equal to the number of atoms in the molecule. Three movements are subtracted from the total because they are saved for the displacement of the center of mass, which keeps the distance and angles between the atoms constant. Another 3 movements are subtracted from the total because they are for the rotations about the 3 principle axes. This means that for nonlinear molecules, there are 3n – 6 normal modes possible. Linear molecules, however, will have 3n – 5 normal modes because it is not possible for internuclear axis rotation, meaning there is one less possible rotation for the molecule. This explain why diatomic molecules only have 1 vibrational frequency, because 3(2) – 5 = 1.
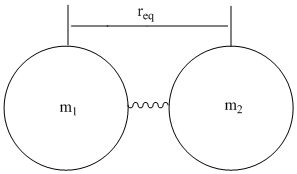
Molecular vibrations are often thought of as masses attached by a spring (Figure \(\PageIndex{2}\)),
and Hook’s law can be applied
\[ F=-kx \]
where
- \(F\) is the resulting force,
- \(x\) is the displacement of the mass from equilibrium \((x = r – r_{eq})\), and
- \(k\) is the force constant, defined as
\[ k=\left (\dfrac{\partial^2V(r)}{\partial r^2} \right)_{r_{eq}}\]
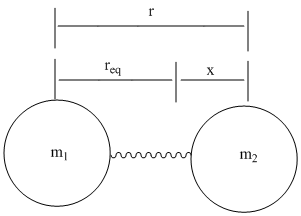
in which \( V(r)=\dfrac{1}{2}k(r-r_{eq}) \), which comes from incorporating Hook’s law to the harmonic oscillator. The diatomic molecule is thought of as two masses (m1 and m2) on a spring, they will have a reduced mass, µ, so their vibrations can be mathematically analyzed.
\[ \mu=\dfrac{m_{1}m_{2}}{m_{1}+m_{2}}\]
When an atom in a molecule is changed to an isotope, the mass number will be changed, so \(µ\) will be affected, but \(k\) will not (mostly). This change in reduced mass will affect the vibrational modes of the molecule, which will affect the vibrational spectrum.
Vibrational energy levels, \(\nu_{e}\), are affected by both k and µ, and is given by
\[ \nu_e=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{\mu}} \]
These vibrational energy levels correspond to the peaks which can be observed in IR and Raman spectra. IR spectra observe the asymmetric stretches of the molecule, while Raman spectra observe the symmetric stretches.
Effects on Experimental Results
When an atom is replaced by an isotope of larger mass, µ increases, leading to a smaller \(\nu_{e}\) and a downshift (smaller wavenumber) in the spectrum of the molecule. Taking the diatomic molecule HCl, if the hydrogen is replaced by its isotope deuterium, µ is doubled and therefore \(\nu_{e}\) will be decreased by \(\sqrt{2}\). Deuterium substitution leads to an isotopic ratio of 1.35-1.41 for the frequencies corresponding to the hydrogen/deuterium vibrations. There will also be a decrease by \(\sqrt{2}\) in the band width and integrated band width for the vibrational spectra of the substituted molecule. Isotopic substitution will affect the entire molecule (to a certain extent), so it is not only the vibrational modes for the substituted atom that will change, but rather the vibrational modes of all the atoms of the molecule. The change in frequency for the atoms not directly invovled in the substitution will not display as large a change, but a downshift can still occur.

When polyaniline (Figure \(\PageIndex{4}\)) is fully deuterated, the vibrational peaks will downshift slightly. The following data was summarized from Quillard et al.
| Type of vibration | Nondeuterated (frequency, cm-1) | Deuterated (frequency, cm-1) |
|---|---|---|
| C-C stretch | 1626 | 1599 |
| C-C stretch | 1581 | 1560 |
| C-H bend – benzenoid ring | 1192 | 876 |
| C-H bend – quinoid ring | 1166 | 856 |
| N-H bend | 1515 | 1085 |
Changing hydrogen to deuterium leads to the largest effect in a vibrational spectrum since the mass is doubled. Other isotopic substitutions will also lead to a shift in the vibrational energy level, but because the mass change is not as significant, µ will not change by much, leading to a smaller change in \(\nu_{e}\). This smaller change in vibrational frequency is seen in the sulfur substitution of sulfur hexafluoride (Figure \(\PageIndex{5}\):), from 32S to 34S. The frequencies as reported by Kolomiitsova et al. are shown below.
| Vibration assignment | 32SF6 (frequency, cm-1) | 34SF6 (frequency, cm-1) |
|---|---|---|
| \(\nu_{3}\) | 939.3 | 922.2 |
| \(\nu_{4}\) | 613.0 | 610.3 |
These two examples show the consistency of downshifted vibrational frequencies for atoms substituted with an isotope of higher mass.
Applications
Substituting atoms with isotopes has been shown to be very useful in determining normal mode vibrations of organic molecules. When analyzing the spectrum of a molecule, isotopic substitution can help determine the vibrational modes specific atoms contribute to. Those normal modes can be assigned to the peaks observed in the spectrum of the molecule. There are specific CH3 rocks and torsions, as well as CH bends that can be identified in the spectrum upon deuterium substitution. Other torsion bands from hydroxyl and amine groups can also be assigned when hydrogen is replaced with deuterium. Experimental data has also shown that using deuterium substitution can help with symmetry assignments and the identification of metal hydrides.
Isotopic substitution can also be used to determine the force constants of the molecule. Calculations can be done using the frequencies of the normal modes in determining these values, based on both calculated frequencies and experimental frequencies.
Researchers have also attempted to contribute peak shape changes and splits in peaks of vibrational spectra to naturally occurring isotopes in molecules. It has been shown, however, that the shape of a peak is not related to the size of the atom, so substitution to an atom of larger mass will not affect the peak shape in the molecule's spectrum. As previously stated, isotopic substitution of atoms of higher mass will not have a significant enough effect on the shifts in frequencies for the corresponding vibrations, so analyzing the frequency shifts of smaller mass isotopes, like deuterium and 13C is necessary.
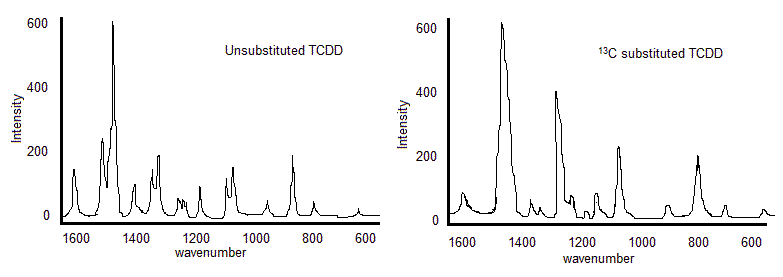
As depicted in the rough representation of the vibrational spectra of the molecule tetrachlorinated dibenzodioxin (TCDD), the 13C substituted TCDD spectrum is slightly downshifted compared to the unsubstituted TCDD spectrum. Although the shifts and split peaks do occur in the spectra of isotopically substituted molecules, not all observed peaks can be attributed to the isotope. This is because the intensities of the peaks shown are not large enough to relate to the natural abundance of the 13C isotope, and not all peaks can be accounted for by the substitution.
References
- Harris, D. C.; Bertolucci, M. D. Symmetry and Spectroscopy; Oxford University Press, Inc.: New York, NY, 1989.
- Kolomiitsova, T. D.; Kondaurov, V. A.; Sedelkova, E. V.; Shchepkin, D. N. Opt. Spectrosc. 2002, 92, 564. DOI: 10.1134/1.1473589
- Mielke, Z.; Sobczyk, L. In Isotope Effects in Chemistry and Biology; Kohen, A., Limbach, H.-H., Eds. 2006, p 281.
- Quillard, S.; Louarn, G.; Buisson, J. P.; Boyer, M.; Lapkowski, M.; Pron, A.; Lefrant, S. Synth. Met. 1997, 84, 805. DOI: 10.1016/S0379-6779(96)04155-0
- Rauhut, G.; Pulay, P. J. Am. Chem. Soc. 1995, 117, 4167. DOI: 10.1021/ja00119a034
- Signorell, R.; Kunzmann, M. K. Chem. Phys. Lett. 2003, 371, 260. DOI: 10.1016/S0009-2614(03)00253-7
Problems
- How many normal modes would be found in CO2? What are the different types of vibrational modes for this molecule?
- If the diatomic molecule HCl, with 1H and 35Cl were substituted with 37Cl, what change occurs to the reduced mass?
- For a nondeuterated hydrofluoric acid diatomic, HF, the vibrational frequency of this molecule is found at 845 cm-1. If the hydrogen atom of this molecule was substituted with deuterium, where would you expect to now find the vibrational frequency?
Answers
- 4; symmetric stretch, asymmetric stretch, and two degenerate bends
- With 37Cl the reduced mass increases from 0.97222 to 0.97368
- DF would have a calculated band at 597.5 cm-1

