Harmonic Oscillator
- Page ID
- 8854
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The harmonic oscillator is a model which has several important applications in both classical and quantum mechanics. It serves as a prototype in the mathematical treatment of such diverse phenomena as elasticity, acoustics, AC circuits, molecular and crystal vibrations, electromagnetic fields and optical properties of matter.
Classical Oscillator
A simple realization of the harmonic oscillator in classical mechanics is a particle which is acted upon by a restoring force proportional to its displacement from its equilibrium position. Considering motion in one dimension, this means
\[ F = −kx \label{1}\]
Such a force might originate from a spring which obeys Hooke’s law, as shown in Figure \(\PageIndex{1}\). According to Hooke’s law, which applies to real springs for sufficiently small displacements, the restoring force is proportional to the displacement—either stretching or compression—from the equilibrium position.
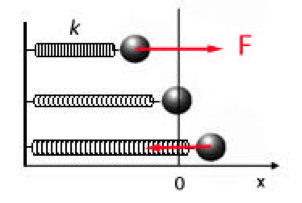
The force constant \(k\) is a measure of the stiffness of the spring. The variable \(x\) is chosen equal to zero at the equilibrium position, positive for stretching, negative for compression. The negative sign in Equation \(\ref{1}\) reflects the fact that \(F\) is a restoring force, always in the opposite sense to the displacement \(x\).
Applying Newton’s second law to the force from Equation \(\ref{1}\), we find \(x\)
\[ F = m \dfrac{d^2 x}{dx^2} = -kx \label{2} \]
where \(m\) is the mass of the body attached to the spring, which is itself assumed massless. This leads to a differential equation of familiar form, although with different variables:
\[ \ddot{x}(t)+ \omega^2x(t)= 0 \label{3}\]
with
\[\omega^2 \equiv \dfrac{k}{m}\]
The dot notation (introduced by Newton himself) is used in place of primes when the independent variable is time. The general solution to Equation \(\ref{3}\) is
\[ x(t) = A\sin ωt + B\cos ωt \label{4}\]
which represents periodic motion with a sinusoidal time dependence. This is known as simple harmonic motion and the corresponding system is known as a harmonic oscillator. The oscillation occurs with a constant angular frequency
\[ \omega = \sqrt{\dfrac{k}{m}}\; \text{radians per second} \label{5} \]
This is called the natural frequency of the oscillator. The corresponding circular (or angular) frequency in Hertz (cycles per second) is
\[ \nu = \dfrac{\omega}{2\pi } = \dfrac{1}{2\pi} \sqrt{\dfrac{k}{m}}\; \text{Hz} \label{6}\]
The general relation between force and potential energy in a conservative system in one dimension is
\[ F =\dfrac{−dV}{dx} \label{7}\]
Thus the potential energy of a harmonic oscillator is given by
\[ V(x) = \dfrac{1}{2}kx^2 \label{8}\]
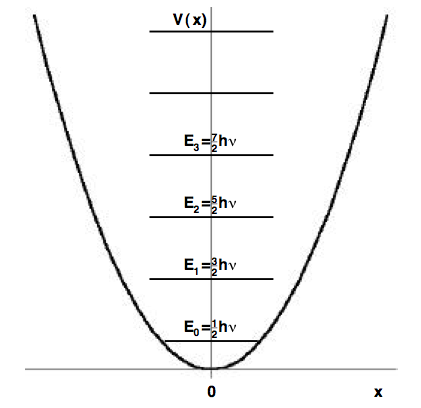
which has the shape of a parabola, as drawn in Figure \(\PageIndex{2}\). A simple computation shows that the oscillator moves between positive and negative turning points \(\pm x_{max}\) where the total energy \(E\) equals the potential energy \(\dfrac{1}{2} k x_{max}^{2}\) while the kinetic energy is momentarily zero. In contrast, when the oscillator moves past \(x = 0\), the kinetic energy reaches its maximum value while the potential energy equals zero.
Harmonic Oscillator in Quantum Mechanics
Given the potential energy in Equation \(\ref{8}\), we can write down the Schrödinger equation for the one-dimensional harmonic oscillator:
\[ -\dfrac{\hbar^{2}}{2m} \psi''(x) + \dfrac{1}{2}kx^2 \psi(x) = E \psi(x) \label{9}\]
For the first time we encounter a differential equation with non-constant coefficients, which is a much greater challenge to solve. We can combine the constants in Equation \(\ref{9}\) to two parameters
\[ \alpha^2 = \dfrac{mk}{\hbar^2}\]
and
\[\lambda = \dfrac{2mE}{\hbar^2\alpha} \label{10}\]
and redefine the independent variable as
\[ \xi = \alpha^{1/2}x \label{11} \]
This reduces the Schrödinger equation to
\[ \psi''(\xi) + (\lambda-\xi^2)\psi(\xi) = 0\label{12} \]
The range of the variable \(x\) (also \(\xi\)) must be taken from \(−\infty\) to \(+\infty\), there being no finite cutoff as in the case of the particle in a box. A useful first step is to determine the asymptotic solution to Equation \(\ref{11}\), that is, the form of \(\psi(\xi)\) as \(\xi\rightarrow\pm\infty\). For sufficiently large values of \(\lvert\xi\rvert\), \(\xi^{2} \gg \lambda\) and the differential equation is approximated by
\[ \psi''(\xi) - \xi^2\psi(\xi) \approx 0 \label{13}\]
This suggests the following manipulation:
\[ \left(\dfrac{d^2}{d\xi^2} - \xi^2 \right) \psi(\xi) \approx \left( \dfrac{d}{d\xi}-\xi \right) \left( \dfrac{d}{d\xi}+\xi \right) \psi(\xi) \approx 0 \label{14}\]
The first-order differential equation
\[ \psi'(\xi) + \xi\psi(\xi)=0 \label{15}\]
can be solved exactly to give
\[ \psi(\xi) = \text{const.}\, e^{-\xi^2/2} \label{16}\]
Remarkably, this turns out to be an exact solution of the Schrödinger equation (Equation \(\ref{12}\)) with \(\lambda=1\). Using Equation \(\ref{10}\), this corresponds to an energy
\[ E=\dfrac{\lambda\hbar^2\alpha}{2m} = \dfrac{1}{2}\hbar\sqrt{\dfrac{k}{m}} = \dfrac{1}{2} \hbar\omega \label{17} \]
where \(\omega\) is the natural frequency of the oscillator according to classical mechanics. The function in Equation \(\ref{16}\) has the form of a Gaussian, the bell-shaped curve so beloved in the social sciences. The function has no nodes, which leads us to conclude that this represents the ground state of the system.The ground state is usually designated with the quantum number \(n = 0\) (the particle in a box is a exception, with \(n = 1\) labeling the ground state). Reverting to the original variable \(x\), we write
\[ \psi_{0}(x) = \text{const} e^{-\alpha x^2/2}\]
with
\[\alpha=(mk/\hbar^2)^{1/2} \label{18}\]
With help of the well-known definite integral (Laplace 1778)
\[\int^{\infty}_{-\infty} e^{- \alpha x^{2}} dx= \sqrt{\dfrac{\pi}{\alpha}} \label{19}\]
we find the normalized eigenfunction
\[\psi_{0}(x)=(\dfrac{\alpha}{\pi})^{1/4} e^{-\alpha x^{2}/2} \label{20}\]
with the corresponding eigenvalue
\[E_{0}=\dfrac{1}{2}\hbar\omega \label{21}\]
Drawing from our experience with the particle in a box, we might surmise that the first excited state of the harmonic oscillator would be a function similar to Equation \(\ref{20}\), but with a node at \(x=0\), say,
\[\psi_{1}(x)=const x e^{-\alpha x^{2}/2} \label{22}\]
This is orthogonal to \(\psi_0(x)\) by symmetry and is indeed an eigenfunction with the eigenvalue
\[E_{1}=\dfrac{3}{2}\hbar\omega \label{23}\]
Continuing the process, we try a function with two nodes
\[\psi_{2}= const (x^{2}-a) e^{-\alpha x^{2}/2} \label{24}\]
Using the integrals tabulated in the Supplement 5, on Gaussian Integrals, we determine that with \(a=\dfrac{1}{2}\) makes \(\psi_{2}(x)\) orthogonal to \(\psi_{0}(x)\) and \(\psi_{1}(x)\). We verify that this is another eigenfunction, corresponding to
\[E_{2}=\dfrac{5}{2}\hbar\omega \label{25}\]
The general result, which follows from a more advanced mathematical analysis, gives the following formula for the normalized eigenfunctions:
\[\psi_{n}(x)=(\dfrac{\sqrt{\alpha}}{2^{n}n!\sqrt{\pi}})^{1/2} H_{n}(\sqrt{\alpha}x) e^{-\alpha x^{2}/2} \label{26}\]
where \(H_{n}(\xi)\) represents the Hermite polynomial of degree \(n\). The first few Hermite polynomials are
\[H_{0}(\xi)=1\]
\[H_{1}(\xi)=2\xi\]
\[H_{2}(\xi)=4\xi^{2}-2\]
\[H_{3}(\xi)=8\xi^{3}-12\xi \label{27}\]
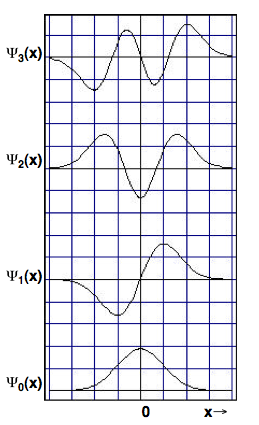
The four lowest harmonic-oscillator eigenfunctions are plotted in Figure \(\PageIndex{3}\). Note the topological resemblance to the corresponding particle-in-a-box eigenfunctions.
The eigenvalues are given by the simple formula
\[E_{n}=\left(n+\dfrac{1}{2}\right)\hbar\omega \label{28}\]
These are drawn in Figure \(\PageIndex{2}\), on the same scale as the potential energy. The ground-state energy \(E_{0}=\dfrac{1}{2}\hbar\omega\) is greater than the classical value of zero, again a consequence of the uncertainty principle. This means that the oscillator is always oscillating.
It is remarkable that the difference between successive energy eigenvalues has a constant value
\[\Delta E=E_{n+1}-E_{n}=\hbar\omega=h\nu \label{29}\]
This is reminiscent of Planck’s formula for the energy of a photon. It comes as no surprise then that the quantum theory of radiation has the structure of an assembly of oscillators, with each oscillator representing a mode of electromagnetic waves of a specified frequency.
Contributors and Attributions
Seymour Blinder (Professor Emeritus of Chemistry and Physics at the University of Michigan, Ann Arbor)

