NMR11. More About Multiplicity
- Page ID
- 4189
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The n + 1 rule (number of lines in a multiplet = number of neighboring H + 1) will work for the majority of problems you may encounter. Occasionally, you may see more complicated coupling. The spectrum of methyl acrylate is a good example. There are a couple of points to note in this spectrum, beginning with the number of peaks.
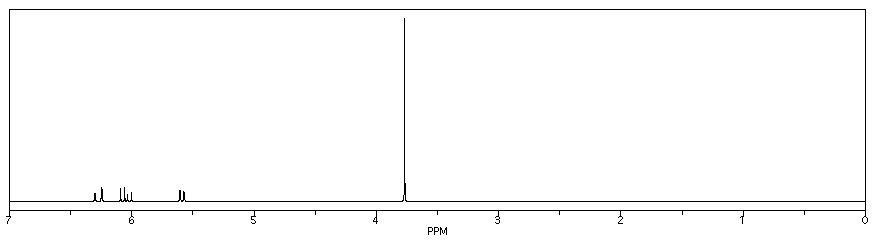
Figure NMR21.1H NMR spectrum of methyl acrylate.
Source: Simulated spectrum.
- In addition, there is a problem with coupling in the vinyl region.
- This pattern is called a "doublet of doublets." The two symmetry-inequivalent neighbors on the other end of the double bond each act as if the other one isn't there. They couple to the proton next to the carbonyl independently, each one splitting the peak for this proton into a separate doublet.
There are a few cases in which this independent coupling will occur rather than the (n+1) type coupling we saw first. Generally, independent coupling occurs when protons are not freely rotating. That can happen if one of the protons is attached to a double-bonded carbon, because we can't rotate around a double bond. It may also happen with protons that are directly attached to the carbons of a ring.
- Sometimes coupling information is depicted as an arrow. This arrow stands for the coupling constant between two protons. The coupling constant is related to the spin of a hydrogen atom. The spin (related to magnetic moment) can be aligned with the external magnetic field (we will show it pointing up) or else against it; no other possibilities are allowed.
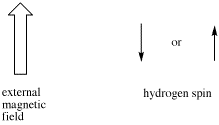
If there are two neighboring hydrogens, both spins could be aligned with the external field, both could be aligned against it, or one could be aligned each way. That means there are three different magnetic combinations that will each have a different effect on the observed proton: increased magnetic field, decreased magnetic field, and no net effect (canceling out).
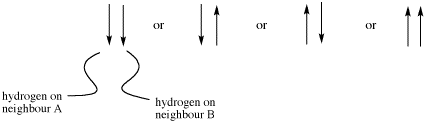
These three combinations result in the observed proton absorbing at three different frequencies, because the frequency it absorbs is sensitive to the magnetic field it experiences. Note that there are two ways to arrive at the middle possibility, with one neighbour spin up and the other spin down. Statistically this possibility is twice as likely as either both spins up or both spins down. It is thus twice as likely that the observed proton experiences that effect, and so the middle line in a triplet is twice as high as the other two lines.
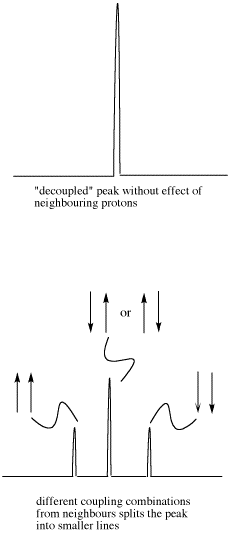
Figure NMR23. Effects of neighboring protons on an observed peak. This case assumes all the neighboring protons have an equivalent effect (they have the same coupling constant with the observed proton).
However, the size of that arrow, the coupling constant, is only the same for two neighboring hydrogens if they have the same spatial relationship with the observed hydrogen. That isn't always true.
- As a result, the two coupling constants are different. We can depict that situation using arrows of different lengths for the two neighboring proton spins. Each spin can be either up or down, but now two opposing spins do not cancel out. The result is four spin combinations of equal probability, not just three.
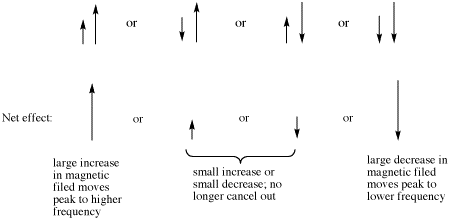
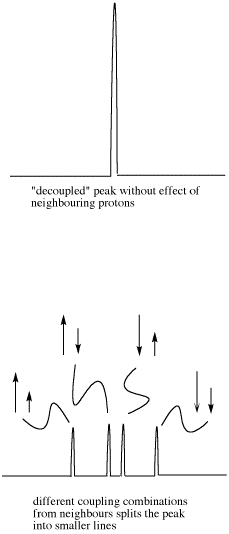
Figure NMR23. Effects of neighboring protons on an observed peak. This case assumes neighboring protons have inequivalent effects (they have differing coupling constants with the observed proton).
The dihedral angle is limited in only a few specific cases:
- As a result, the two coupling constants are different. We can depict that situation using arrows of different lengths for the two neighboring proton spins. Each spin can be either up or down, but now two opposing spins do not cancel out. The result is four spin combinations of equal probability, not just three.
- Sometimes coupling information is depicted as an arrow. This arrow stands for the coupling constant between two protons. The coupling constant is related to the spin of a hydrogen atom. The spin (related to magnetic moment) can be aligned with the external magnetic field (we will show it pointing up) or else against it; no other possibilities are allowed.
- This pattern is called a "doublet of doublets." The two symmetry-inequivalent neighbors on the other end of the double bond each act as if the other one isn't there. They couple to the proton next to the carbonyl independently, each one splitting the peak for this proton into a separate doublet.


