Phase Cycling and Coherence Transfer Pathways
- Page ID
- 17016
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In NMR simply throwing a string of pulses with random phases is a recipe for disaster. Phase cycling is a way to choose the proper coherence pathway in order to acquire the NMR signal which has the interactions you are trying to acquire. Additionally, phase cycling eliminates artifacts that can appear in the NMR spectrum which are not real NMR signals.
NMR Artifact
Two problems are commonly encountered during detection of the NMR signal. This first occurs when the detector should be detecting zero but actually records a non-zero value. This is known as a receiver baseline error, commonly known as a zero glitch. The other type of artifact occurs from errors in the quadrature detection of the NMR signal. NMR spectra can contain both of these and can severely complicate spectra. Fortunately, we can eliminate these by employing phase cycling.
Zero Glitch
If the detector is turned on and the voltage is non-zero, then a spike will form in the exact center of the spectrum. A zero glitch is easy to check for by changing the carrier frequency. If the spike moves to the center of the spectrum, you have a zero glitch.
Quadrature Ghost (Image)
From our discussion on the NMR receiver, quadrature detection is used. In this, the frequency is split and a reference phase is superimposed on one of the carrier frequencies. Successful recombination of the frequencies is of the form
\[S=\cos+i\sin\]
and the resulting Fourier Transform is a peak at a certain frequency. However, when the phase is not set correctly, or the efficiency of the hardware changes, the signal now has a different phase (not 90°). This results in a signal at the exact opposite frequency.
Coherence Transfer Pathway
Conferences are developed by the application of pulses of a phase \(\phi\). As our discussion from the Bloch equations, three different conferences can develop p=-1,0,+1 with the application of the pulse, depending on the efficiency of the coherence transfer. We also saw that the relaxation processes decay the coherence. Additionally, the coherence will not change without the application of a pulse. We can then construct a coherence transfer diagram which illustrates the coherence path as a function of the pulse sequence.
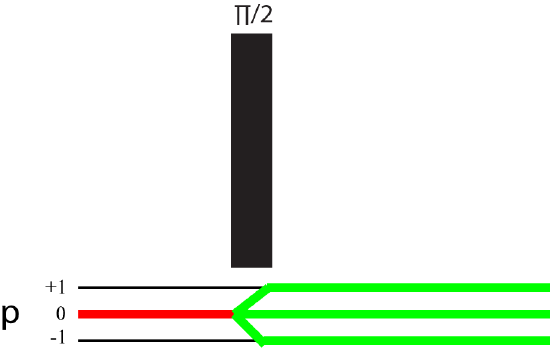
As you can see from above, there are multiple coherences at the end of the pulse sequence. In fact, for a spin=1/2 system with n pulses, 3n coherence pathways evolve! We must then select the proper coherence to detect! Luckily, most receivers are equipped to only detect on the -1 coherence. This limits detection to only a fraction of the total coherences that evolve. Therefore, we must develop a way to selectively obtain the coherences with the interactions we want to probe.
Nested Phase Cycling
Phase cycling is a way to selectively extract a single coherence that has evolved with a selected pathway. The only way to change a coherence is to apply a pulse by phase \(\phi\). Therefore, we must know the coherence pathway we are interested in and we need to set the phases of the pulses and receiver accordingly. Luckily it is fairly easy to calculate which phases are needed. We know that the coherence must be =-1 at the end of the pulse sequence for the signal to be detected by the receiver. The master equation is listed below
\[\phi_{rec}=-\sum_{m=1}^{M_T}\Delta p \phi_m\]
where \(\phi_R\) is the receiver phase, \(\Delta p\) is the desired change in coherence and \(\phi_m\) is the phase of the pulse m.
If we only ever used one pulse, then only three coherences would evolve. However, with multiple pulses, multiple signals will be at the -1 coherence during detection. We can average these by changing the phase \(\phi_m\). The phase should be incremented, at most by
\[\Delta \phi_m=\frac{2\pi}{n_m}\]
where
\[n_m=\Delta p_m^{(max)}-\Delta p_m^{(min)} +1\]
Let's consider the pulse sequence in figure 1. Let's also assume we do not have a perfect detector, and some of the magnetization from the +1 and 0 coherences can be detected.
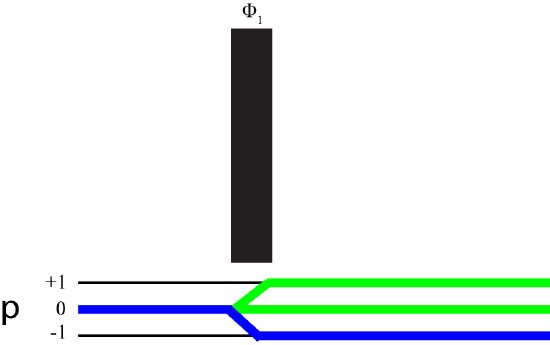
Our desired pathway is 0 to -1. \(\Delta p_1^{(max)} =1\) and \(\Delta p_1^{(min)}=-1\) Then n1=3. Therefore we need to increment \(\phi\) by steps of 120^\(\circ\) to create the phase cycle. Our desired \(\Delta p = -1-0=-1\). Thus
\[\phi_{rec}=\phi_1\]
Our full phase cycle is for both \(\phi_{rec}\) and \(\phi_1\) = 0, 120, 240. Therefore 3 scans are needed to complete the phase cycle. Experiments should have a multiple of 3 to make sure a proper spectrum is acquired. Let's take a look at a more complex pulse sequence, the Hahn echo sequence. The pulse sequences with the desired pathway is outline below.
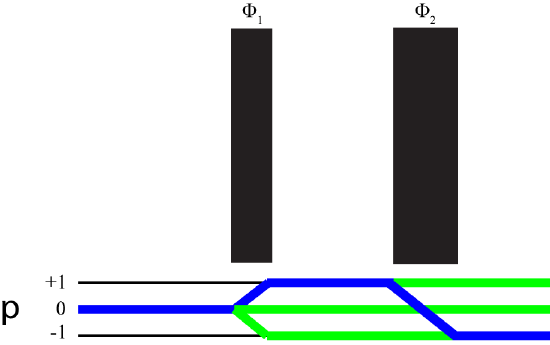
We must once again calculate the the master equation, however we now have to consider the second pulse. Lets first break the sequence up into 2 steps, the first step will be for \(\phi_1\) and the second for \(\phi_2\). For \(\phi_1\):
\[\Delta p_1=1-0=1\]
\[n_m==1-(-1)+1=3\]
\[\Delta \phi_1=\frac{2\pi}{n_m}=120^\circ\]
For \(\phi_2\):
\[\Delta p_2=-1-1=-2\]
\[n_m==1-(-1)+1=3\]
\[\Delta \phi_1=\frac{2\pi}{n_m}=120^\circ\]
Then
\[\phi_{rec}=-(\phi_1-2\phi_2)\]
and the phase cycle would be
\[\begin{matrix}\phi_1 & = & 0^\circ & 120^\circ & 240^\circ & 0^\circ & 120^\circ & 240^\circ & 0^\circ & 120^\circ & 240^\circ \\ \phi_2 & =& 0^\circ & 0^\circ & 0^\circ & 120^\circ & 120^\circ & 120^\circ & 240^\circ & 240^\circ & 240^\circ \\ \phi_{rec}&=&0^\circ& 240^\circ &120^\circ &240^\circ &120^\circ &0^\circ &120^\circ & 0^\circ & 240^\circ & \end{matrix}\]
As you can see from above, this is a nested phase cycle, in which the three steps of \(\phi_1\) are incremented successively, while \(\phi_2\) is incremented only after completion of a full phase cycle is completed for \(\phi_1\) while this creates a robust phase cycle, there are several shortcuts which enable the phase cycles to be shortened. For instance, if no quadrature ghosts are detected, meaning only to -1 coherence is observed, then only one pulse needs to be phase cycled. This gives
\[\begin{matrix}\phi_1 & = & 0^\circ & 120^\circ & 240^\circ \\ \phi_{rec}&=&0^\circ& 240^\circ &120^\circ & \end{matrix}\]
or
\[\begin{matrix}\phi_2 & = & 0^\circ & 120^\circ & 240^\circ \\ \phi_{rec}&=&0^\circ& 240^\circ &120^\circ & \end{matrix}\]
Note that the phases for \(\phi_1\) and \(\phi_2\) are obtained when the opposing \(\phi\)=0
Phase Cycling with Coherences>1
Until now, we have considered a spin=1/2 nucleus with coherences = -1, 0 ,+1, which we readily obtained from the spherical representation of the Bloch equations. However, the Bloch equations are only valid for a single uncouple spin, which is not the case for most systems. Therefore, access to higher coherences are possible for coupled spin=1/2 nuclei as well as quadrupolar nuclei.

