Bonding Theory for UV-visible Absorption Spectra
- Page ID
- 3745
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page takes an introductory look at two areas of bonding theory needed for a proper understanding of how organic compounds absorb some of the UV or visible light that passes through them.
It looks simply at anti-bonding orbitals, and what is meant by conjugation in compounds and how it contributes to the delocalization of electrons.
Anti-bonding orbitals
Bonding and anti-bonding orbitals in a simple hydrogen molecule
I am assuming that you know how a simple covalent bond between two atoms forms. Half-filled atomic orbitals on each atom overlap in space to form a new orbital (a molecular orbital) containing both electrons. In the case of two hydrogen atoms, each has one electron in the 1s orbital. These come together to make a new orbital surrounding both of the hydrogen nuclei.

It is important to understand exactly what this molecular orbital means. The two electrons are most likely to be found in this region of space - and the most likely place to find them within this space is on the line between the two nuclei.
The molecule holds together because both nuclei are strongly attracted to this same pair of electrons. This most simple of bonds is called a sigma bond - a sigma bond is one where the electron pair is most likely to be found on the line between the two nuclei.
However . . . This is all a bit of a simplification! Molecular orbital theory demands that if you start with two atomic orbitals, you must end up with two molecular orbitals - and we seem to be only producing one. A second molecular orbital is formed, but in most cases (including the hydrogen molecule) it is left empty of electrons. It is described as an anti-bonding orbital. The anti-bonding orbital has a quite different shape and energy from the bonding orbital.
The next diagram shows the relative shapes and energies of the various atomic and molecular orbitals when two hydrogen atoms combine.
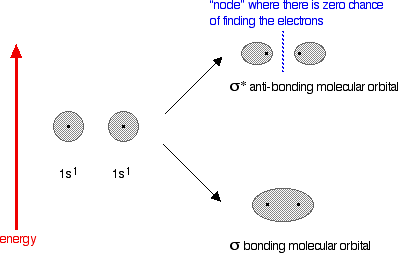
An anti-bonding orbital is always shown by the use of a star after its symbol.
Notice that when a bonding orbital forms, it is at a lower energy than the original atoms. Energy is released when the bonding orbital is formed, and the hydrogen molecule is more energetically stable than the original atoms. However, an anti-bonding orbital is less energetically stable than the original atoms.
A bonding orbital is stable because of the attractions between the nuclei and the electrons. In an anti-bonding orbital there are no equivalent attractions - instead you get repulsions. There is very little chance of finding the electrons between the two nuclei - and in fact half-way between the nuclei there is zero chance of finding them. There is nothing to stop the two nuclei from repelling each other apart.
So in the hydrogen case, both of the electrons go into the bonding orbital, because that produces the greatest stability - more stable than having separate atoms, and a lot more stable than having the electrons in the anti-bonding orbital.
Why doesn't helium form an He2 molecule?
You might reasonably say that helium can't form an He2 molecule because it doesn't have any unpaired electrons to share. Fine! But let's also look at it from the point of molecular orbital theory. The diagram for helium is just a small modification of the last one.
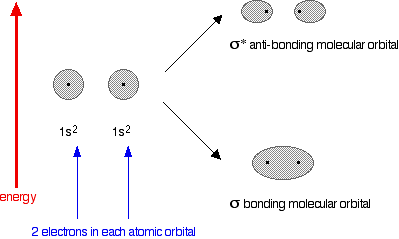
This time we have a total of 4 electrons in the original atomic orbitals. Two atomic orbitals have to form two molecular orbitals. That means that this time, we would have to use both the bonding and anti-bonding molecular orbitals to accommodate them.
But any gain in energetic stability due to the formation of the bonding orbitals would be countered by the loss of energetic stability because of the anti-bonding ones. There is no energetic advantage in He2 forming - and so it doesn't.
Anti-bonding orbitals in double bonds
You are probably familiar with a picture of the double bond in ethene shown as:
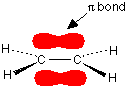
The pi bond shown in red is, of course, a normal bonding orbital. It was formed by sideways overlap between a half-filled p-orbital on each of the two carbon atoms. Remember that the two red shapes shown in the diagram are part of the same pi bonding orbital. But if you overlap two atomic orbitals, you must get two molecular orbitals according to molecular orbital theory. The second one is an anti-bonding pi orbital - and we never draw it under normal circumstances.
The anti-bonding pi orbital is (just like the anti-bonding sigma one) at a higher energy than the bonding orbital - and so isn't used to hold electrons. Both of the electrons in the pi bond are found in the pi bonding orbital.
Summarizing the relative energies of various kinds of orbitals
The next diagram gives a general impression of how the energies of various types of orbital relate to each other in the sort of compounds we will be looking at when we try to explain the absorption of light. It is not to scale. You will find that a new sort of orbital has crept into the diagram - labelled "n" (for non-bonding). The sort of non-bonding orbitals that we will be interested in contain lone pairs of electrons on, for example, oxygen, nitrogen and halogen atoms.
So . . . think of non-bonding orbitals as those containing lone pairs of electrons at the bonding level.
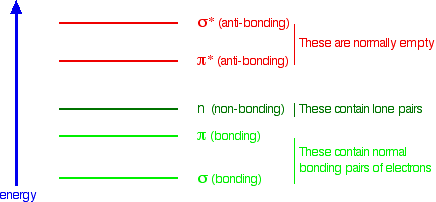
When light passes through a compound, some of the energy in the light kicks an electron from one of the bonding or non-bonding orbitals into one of the anti-bonding ones. The energy gaps between these levels determine the frequency (or wavelength) of the light absorbed, and those gaps will be different in different compounds. This is covered in detail on another page.
Conjugation
We are going to leave explaining what conjugation is for a while - it is necessary to look at some more bonding first.
The simple ethene double bond
To understand about conjugated double bonds, you first need to be sure that you understand simple double bonds. Ethene contains a simple double bond between two carbon atoms, but the two parts of this bond are different. Part of it is a simple sigma bond formed from end-to-end overlap between orbitals on each carbon atom, and part is caused by sideways overlap between a p-orbital on each carbon.
The important diagram is the one leading up to the formation of the pi bond - where the two p-orbitals are overlapping sideways:
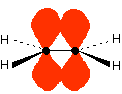
. . . giving the familiar pi bond.

Conjugated double bonds in buta-1,3-diene
Bonding in buta-1,3-diene
Buta-1,3-diene has the structure:
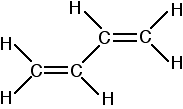
Now picture the formation of the various molecular orbitals as if you were thinking about two ethene molecules joined together. You would have sigma bonds formed by the end-to-end overlap of various orbitals on the carbons and hydrogens. That would leave you with a p-orbital on each carbon atom.
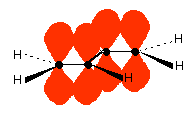
Those p-orbitals will overlap sideways - all of them! A system of delocalised pi bonds is formed, similar to the benzene case that you are probably familiar with. The diagram shows one of those molecular orbitals.
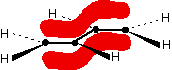
To stress again - the diagram shows only one of the delocalised molecular orbitals. Remember that both of the red bits in the diagram are part of the same orbital. The interaction of the two double bonds with each other to produce a delocalised system of pi electrons over all four atoms is known as conjugation. Conjugation in this context literally means "joining together".
In reality, if you start by overlapping four atomic orbitals, you will end up with four molecular orbitals. The four electrons will go into the two lowest energy of these - two in each. That means that you get two pi bonding orbitals. We just draw one of these for simplicity - the other one has a different shape.
There are also two pi anti-bonding orbitals, but these are normally empty. For most purposes, we ignore these entirely - although not for this topic because energy from light can promote electrons from a pi bonding orbital into one of the anti-bonding orbitals (as you will see on the next page).
Recognizing conjugated double bonds in a molecule
You can recognize the presence of conjugated double bonds in a molecule containing more than one double bond because of the presence of alternating double and single bonds. The double bonds don't have to be always between carbon atoms. All of the following molecules contain conjugated double bonds, although in the last case, the conjugation doesn't extend over the whole molecule:
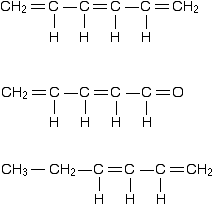
However, although the next molecule contains two double bonds, they aren't conjugated. They are separated by two single bonds.
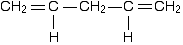
The reason why it is important to have the double and single bonds alternating is that this is the only way you can get all the p-orbitals overlapping sideways. In the last case, you will get sideways overlap at each end of the molecule to get two individual pi bonds. But the extra single bond in the middle stops them from interacting with each other.
delocalization extending beyond conjugated double bonds
Benzene rings
You are almost certainly familiar with the delocalization which occurs in a benzene ring. If you think about benzene using the Kelulé structure, you have a perfect system of alternating single and double bonds around the molecule.
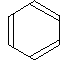
These conjugate to give the familiar delocalised pi system.
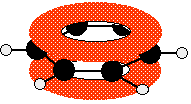
Once again, remember that this only shows one of the molecular orbitals formed. There will actually be three bonding pi orbitals and three anti-bonding ones - because they arise from combining a total of six atomic orbitals. The extra bonding orbitals aren't usually drawn.
Phenylamine and phenol
delocalization can also extend beyond pi bonds to include lone pairs on atoms like nitrogen or oxygen. Two simple examples of this are phenylamine (aniline) and phenol. Writing these using the Kekulé structure for benzene:
You can see the alternating double and single bonds around the benzene ring. This conjugation leads to the familiar delocalised electron system in benzene which we usually show as:

But the delocalization doesn't stop at the ring. It extends out to the nitrogen or oxygen atoms. In the phenylamine case, there is a lone pair on the nitrogen atom which can overlap with the ring electrons . . .
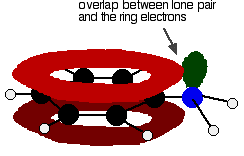
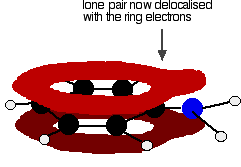
. . . leading to delocalization which takes in both ring and nitrogen.
Exactly the same thing happens with phenol. One of the oxygen lone pairs overlaps with the ring electrons. The other one is pointing in the wrong direction to get involved.
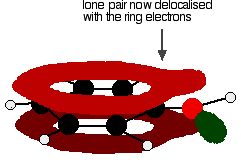
So . . . if you are trying to work out how far delocalization extends in a molecule, don't forget to look for atoms with lone pairs that might get involved in the delocalization.
Other groups to look out for
Look especially for benzene rings with groups attached which contain double bonds. Let's start with a couple of simple ones - phenylethene (styrene) and benzaldehyde.
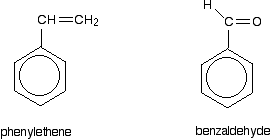
In each case, you've got delocalization over the ring. Does it extend to the attached group? Do you have anything like alternating single and double bonds? Yes, you do. You have the double bond in the side group, then a single bond, then the ring delocalization. Looking at this in the phenylethene case, and imagining the arrangement of orbitals just before delocalization over the side group:
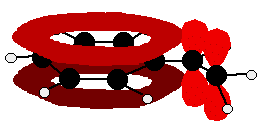
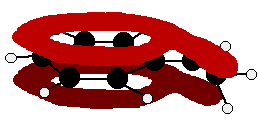
You can see that the double bond and ring electrons will overlap to form a delocalised system looking something like this:
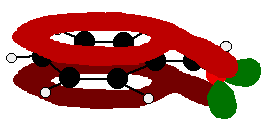
The benzaldehyde case is very similar, except that this time instead of the CH2 group at the end there is an oxygen with two lone pairs. The delocalization is just the same.
Be careful, though! Remember that to get this extended delocalization, any double bond in the side chain must be able to conjugate with the ring electrons - the two bits must be close enough to join together. Molecules like those in the next diagram don't have the delocalization extending out into the side chain. The extra CH2 group prevents the necessary sideways overlap between the p orbitals of the double bond and the ring electrons.
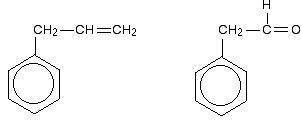
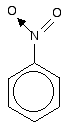
The other side group which it would be useful to know about is the nitro group, NO2 - for example in nitrobenzene.
The bonding in the nitro group is surprisingly awkward to work out. It is often shown with a double bond between the nitrogen and one of the oxygens, and a co-ordinate (dative covalent) bond to the other.
This structure is actually misleading. Both nitrogen-oxygen bonds are identical and the group already has delocalization. This is often shown as:
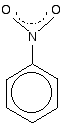
The dotted half-circle suggests the delocalization. Think of it as being like the circle you draw in the middle of the benzene hexagon. This delocalization is just one single bond away from the ring delocalization. You get conjugation between the two, and the delocalization takes in the whole molecule.
A case to beware of
Another case we need to look at (because it occurs in a molecule we'll explore on the next page) is an SO3- group attached to a benzene ring.
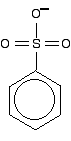
It looks as if the double bonds are in just the right position relative to the ring for the delocalization to extend out over this group. However, I have been told on good authority that the delocalization doesn't extend from the side group into the ring. I can't, though, find any reference to this anywhere on the web or in the textbooks that I have available. The bonding in the sulfonate group isn't at all easy to describe in orbital terms. In fact, it is most easily explained in terms of co-ordinate (dative covalent) bonds, but introducing that now is just complicating things pointlessly.
Summary
When you are trying to work out how far delocalization extends in a molecule, look for:
- alternating double and single bonds - not just between carbon and carbon, but including C=O, C=N, N=N, N=O. Carbon-carbon triple bonds can also be involved in place of a carbon-carbon double bond.
- benzene rings.
- possible involvement of lone pairs on nitrogen or oxygen.
- NO2 groups.
And finally . . . why does all this matter? The wavelength of UV or visible light absorbed by organic compounds depends largely on the extent of delocalization in the molecules. That means that you may well have to look at an unfamiliar molecule and make a reasonable estimate of whether it is highly delocalised or not very delocalised. It will always be pretty clear-cut at this level, so don't worry too much about it!


