Electromagnetic Radiation

This page is a basic introduction to the electromagnetic spectrum sufficient for chemistry students interested in UV-visible absorption spectroscopy. If you are looking for any sort of explanations suitable for physics courses, then I'm afraid this isn't the right place for you.

Light as a wave form

Any wave is essentially just a way of shifting energy from one place to another - whether the fairly obvious transfer of energy in waves on the sea or in the much more difficult-to-imagine waves in light.

In waves on water, the energy is transferred by the movement of water molecules. But a particular water molecule doesn't travel all the way across the Atlantic - or even all the way across a pond. Depending on the depth of the water, water molecules follow a roughly circular path. As they move up to the top of the circle, the wave builds to a crest; as they move down again, you get a trough.

The energy is transferred by relatively small local movements in the environment. With water waves it is fairly easy to draw diagrams to show this happening with real molecules. With light it is more difficult.

The energy in light travels because of local fluctuating changes in electrical and magnetic fields - hence "electromagnetic" radiation.

Wavelength, frequency and the speed of light

If you draw a beam of light in the form of a wave (without worrying too much about what exactly is causing the wave!), the distance between two crests is called the wavelength of the light. (It could equally well be the distance between two troughs or any other two identical positions on the wave.)

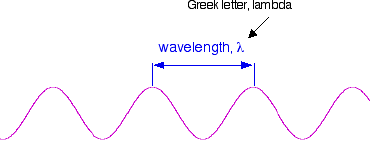
You have to picture these wave crests as moving from left to right. If you counted the number of crests passing a particular point per second, you have the frequency of the light. It is measured in what used to be called "cycles per second", but is now called Hertz, Hz. Cycles per second and Hertz mean exactly the same thing.

Orange light, for example, has a frequency of about 5 x 10¹⁴ Hz (often quoted as 5 x 10⁸ MHz - megahertz). That means that 5 x 10¹⁴ wave peaks pass a given point every second. Light has a constant speed through a given substance. For example, it always travels at a speed of approximately 3 x 10⁸ meters per second in a vacuum. This is actually the speed that all electromagnetic radiation travels - not just visible light.

There is a simple relationship between the wavelength and frequency of a particular color of light and the speed of light:

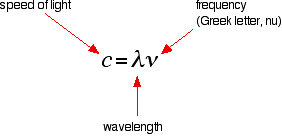
. . . and you can rearrange this to work out the wavelength from a given frequency and vice versa:

\[ \lambda = \dfrac{c}{\nu}\]

\[ \nu= \dfrac{c}{\lambda}\]

These relationships mean that if you increase the frequency, you must decrease the wavelength.

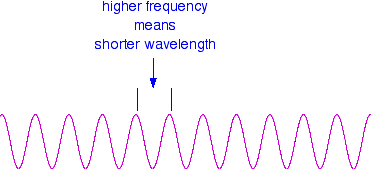
Compare this diagram with the similar one above. . . and, of course, the opposite is true. If the wavelength is longer, the frequency is lower. It is really important that you feel comfortable with the relationship between frequency and wavelength. If you are given two figures for the wavelengths of two different colors of light, you need to have an immediate feel for which one has the higher frequency.

For example, if you were told that a particular color of red light had a wavelength of 650 nm, and a green had a wavelength of 540 nm, it is important for you to know which has the higher frequency. (It's the green - a shorter wavelength means a higher frequency. Don't go on until that feels right!)

The frequency of light and its energy

Each particular frequency of light has a particular energy associated with it, given by another simple equation:

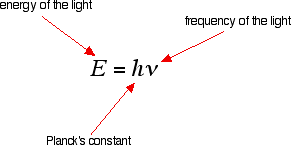
You can see that the higher the frequency, the higher the energy of the light. Light which has wavelengths of around 380 - 435 nm is seen as a sequence of violet colours. Various red colours have wavelengths around 625 - 740 nm. Which has the highest energy?

The light with the highest energy will be the one with the highest frequency - that will be the one with the smallest wavelength. In other words, violet light at the 380 nm end of its range.

The Electromagnetic Spectrum

Visible light

The diagram shows an approximation to the spectrum of visible light.

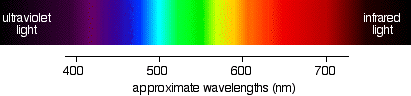
The main colour regions of the spectrum are approximately:

colour region	wavelength (nm)
violet	380 - 435
blue	435 - 500
cyan	500 - 520
green	520 - 565
yellow	565 - 590
orange	590 - 625
red	625 - 740

Don't assume that there is some clear cut-off point between all these colours. In reality, the colours just merge seamlessly into one another - much more seamlessly than in my diagram!

Placing the visible spectrum in the whole electromagnetic spectrum

The electromagnetic spectrum doesn't stop with the colors you can see. It is perfectly possible to have wavelengths shorter than violet light or longer than red light. On the spectrum further up the page, I have shown the ultra-violet and the infra-red, but this can be extended even further into x-rays and radio waves, amongst others. The diagram shows the approximate positions of some of these on the spectrum.

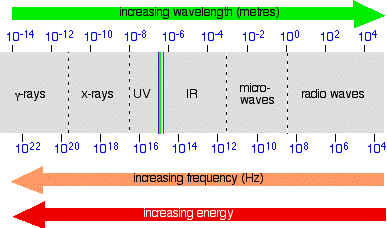
Once again, don't worry too much about the exact boundaries between the various sorts of electromagnetic radiation - because there are no boundaries. Just as with visible light, one sort of radiation merges into the next. Just be aware of the general pattern.

Also be aware that the energy associated with the various kinds of radiation increases as the frequency increases.