Radial Nodes

A radial node is a sphere (rather than an angular node which is a flat plane) that occurs when the radial wavefunction for an atomic orbital is equal to zero or changes sign.

Introduction

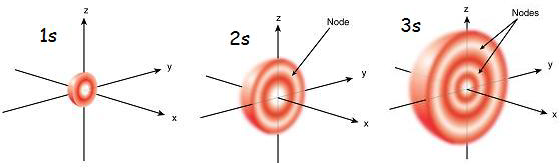
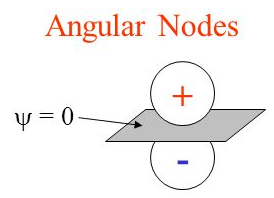
There are two types of nodes within an atom: angular and radial. Angular nodes are or will be discussed in another section; this section is dedicated to the latter. Radial nodes, as one could guess, are determined radially. Using the radial probability density function, places without electrons, or radial nodes, can be found. A quick comparison of the two types of nodes can be seen in the diagram above. Angular nodes are either x, y, and z planes where electrons aren’t present while radial nodes are sections of these axes that are closed off to electrons.

For atomic orbitals, the wavefunction can be separated into a radial part and an angular part so that it has the form

\[Ψ(r,θ,ϕ)=R(r)Y(θ,ϕ)\]

where \(R(r)\) is the radial component which depends only on the distance from the nucleus and Y(θ,ϕ) is the angular component. The radial nodes consist of spheres whereas the angular nodes consist of planes (or cones).

Figure 1: Various s orbitals. All of these orbitals have ℓ = 0, but they have different values for n. The first orbital has n = 1, and thus is small and has no nodes. The second orbital has n = 2, and thus is larger and has one node. The third orbital has n = 3, and thus is even larger and has two nodes. IMage used with permission (CC SA-BY 3.0; CK-12 Foundation).

A radial node will occur where the radial wavefunction, \(R(r)\), equals zero. At a node the probability of finding an electron is zero; which means that we will never find an electron at a node.

Basic description

To solve for the number of radial nodes, the following simple equation can be used.

Radial Nodes = n - 1 - ℓ

The ‘n’ accounts for the total amount of nodes present. The ‘-1’ portion accounts for the node that exists at the ends. (A half of one node exists at one end and since there are two ends, there’s a total of one node located at the ends.) The azimuthal quantum number determines the shape of the orbital and how many angular nodes there are. The remaining number, which currently doesn’t have a symbol, is the amount of radial nodes which are present. Here’s a quick example:

Radial nodes occur as the principle quantum number (n) increases and the number of radial nodes depends on the principle quantum number (n) and the number of angular nodes (l). The total number of nodes is found using

Total Nodes=n-1

From knowing the total nodes we can find the number of radial nodes by using

Radial Nodes=n-l-1

which is just the total nodes minus the angular nodes.

Example \(\PageIndex{1}\):

first shell (n=1) number of nodes= n-1=0 so there aren't any nodes

second shell (n=2) number of nodes=n-1=1 total nodes

for 2s orbital l=0 so there are 0 angular nodes and 1 radial node

for 2p orbital l=1 so there is 1 angular node and 0 radial nodes

third shell (n=3) number of nodes=n-1=2 total nodes

for 3s orbital l=0 so there are 0 angular nodes and 2 radial nodes

for 3p orbital l=1 so there is 1 angular node and 1 radial node

for 3d orbital l=2 so there are 2 angular nodes and 0 radial nodes

Exercise \(\PageIndex{1}\)

Find the radial nodes in a 3p orbital.

Answer

For the 3p orbital, the ‘3’ means that ‘n’ = 3 and ‘p’ shows that ‘ℓ’ = 1. ‘ℓ’ also equals the number of angular nodes which means there is one angular node present. Using the equation for radial nodes, n - ℓ - 1 = 3 - 1 - 1 = 1. Thus there is one radial nodes. The following section will show how to determine radial nodes in a more complex way.

Advanced description

We can calculate how many nodes there will be based off the equation above, however we can also see this from the wavefunction. For example the wavefunction for the Hydrogen atom 3d orbital:

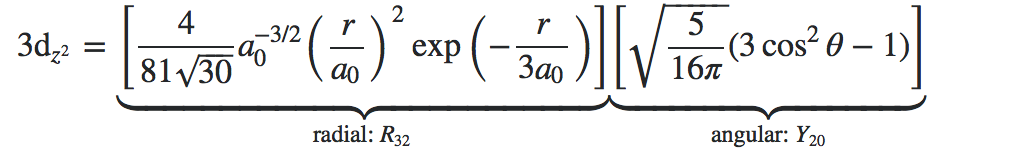
From the equation above we can see that the number of total nodes is n-1=2 and the number of angular nodes (l)=2 so the number of radial nodes is 0. From the wavefunction for the \(3dz^2\) orbital, we can see that (excluding r=0 and as r goes to infinity) the radial wavefunction will never equal to zero so there are 0 radial nodes for this orbital. For the angular wavefunction, we see there will be an angular node when \(3cos^2θ-1=0\); which corresponds to the 2 solutions θ=54.7º and 125.3º.

As stated above, we know that at a node the probability of finding an electron is zero. The diagram below shows that as n increases, the number of radial nodes increases.

Figure 2: The radial probability distribution of finding an electron in the 1s, 2s and 3s orbitals. For each S orbital, the probability of finding an electron is zero when r equals zero and as r goes to infinity. (https://ch301.cm.utexas.edu/section2...tribution.html)

From Figure 2 we can see that for the 1s orbital there are not any nodes (the curve for the 1s orbital doesn't equal zero probability other than at r=0 and as r goes to infinity). This is expected since n-l-1 for the 1s orbital is 1-0-1=0 radial nodes. For the 2s orbital, the curve has zero probability at 1 point (again other than r=0 and as r goes to infinity); which is consistent with the n-l-1 for the 2s orbital 2-0-1=1 radial node. For the 3s orbital, the curve has zero probability at 2 points; which is consistent with the n-l-1 for the 3s orbital 3-0-1=2 radial nodes.

But what about for molecular orbitals?

To separate the wavefunction into a radial part and an angular part, the system needs to be spherically symmetric. For an atom this is the case but a molecule can never be. Thus radial nodes do not exist for molecular orbitals.

Contributors and Attributions

• Rachel Schonwit