Units of Concentration
- Page ID
- 1624
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Solutions are homogeneous mixtures containing one or more solutes in a solvent. The solvent that makes up most of the solution, whereas a solute is the substance that is dissolved inside the solvent.
Relative Concentration Units
Concentrations are often expressed in terms of relative unites (e.g. percentages) with three different types of percentage concentrations commonly used:
- Mass Percent: The mass percent is used to express the concentration of a solution when the mass of a solute and the mass of a solution is given: \[\text{Mass Percent}=\dfrac{\text{Mass of Solute}}{\text{Mass of Solution}} \times 100\% \label{1}\]
- Volume Percent: The volume percent is used to express the concentration of a solution when the volume of a solute and the volume of a solution is given: \[\text{Volume Percent}= \dfrac{\text{Volume of Solute}}{\text{Volume of Solution}} \times 100\% \label{2}\]
- Mass/Volume Percent: Another version of a percentage concentration is mass/volume percent, which measures the mass or weight of solute in grams (e.g., in grams) vs. the volume of solution (e.g., in mL). An example would be a 0.9%( w/v) \(NaCl\) solution in medical saline solutions that contains 0.9 g of \(NaCl\) for every 100 mL of solution (see figure below). The mass/volume percent is used to express the concentration of a solution when the mass of the solute and volume of the solution is given. Since the numerator and denominator have different units, this concentration unit is not a true relative unit (e.g. percentage), however it is often used as an easy concentration unit since volumes of solvent and solutions are easier to measure than weights. Moreover, since the density of dilute aqueous solutions are close to 1 g/mL, if the volume of a solution in measured in mL (as per definition), then this well approximates the mass of the solution in grams (making a true reletive unit (m/m)).
\[\text{Mass/Volume Percent}= \dfrac{\text{Mass of Solute (g)}}{\text{Volume of Solution (mL)}} \times 100\% \label{3}\]
For example, In the United States, alcohol content in spirits is defined as twice the percentage of alcohol by volume (v/v) called proof. What is the concentration of alcohol in Bacardi 151 spirits that is sold at 151 proof (hence the name)?

Solution
It will have an alcohol content of 75.5% (w/w) as per definition of "proof".
When calculating these percentages, that the units of the solute and solution should be equivalent units (and weight/volume percent (w/v %) is defined in terms of grams and mililiters).
| You CANNOT plug in… | You CANNOT plug in… |
|---|---|
| (2 g Solute) / (1 kg Solution) | (2 g Solute) / (1000 g Solution) |
| or (0.002 kg Solute) / (1 kg Solution) | |
| (5 mL Solute) / (1 L Solution) | (5 mL Solute) / (1000 mL Solution) |
| or (0.005 L Solute) / (1 L Solution) | |
| (8 g Solute) / (1 L Solution) | (8 g Solute) / (1000 mL Solution) |
| or (0.008 kg Solute) / (1 L Solution) |
Dilute Concentrations Units
Sometimes when solutions are too dilute, their percentage concentrations are too low. So, instead of using really low percentage concentrations such as 0.00001% or 0.000000001%, we choose another way to express the concentrations. This next way of expressing concentrations is similar to cooking recipes. For example, a recipe may tell you to use 1 part sugar, 10 parts water. As you know, this allows you to use amounts such as 1 cup sugar + 10 cups water in your equation. However, instead of using the recipe's "1 part per ten" amount, chemists often use parts per million, parts per billion or parts per trillion to describe dilute concentrations.
- Parts per Million: A concentration of a solution that contained 1 g solute and 1000000 mL solution (same as 1 mg solute and 1 L solution) would create a very small percentage concentration. Because a solution like this would be so dilute, the density of the solution is well approximated by the density of the solvent; for water that is 1 g/mL (but would be different for different solvents). So, after doing the math and converting the milliliters of solution into grams of solution (assuming water is the solvent): \[\dfrac{\text{1 g solute}}{\text{1000000 mL solution}} \times \dfrac{\text{1 mL}}{\text{1 g}} = \dfrac{\text{1 g solute}}{\text{1000000 g solution}}\] We get (1 g solute)/(1000000 g solution). Because both the solute and the solution are both now expressed in terms of grams, it could now be said that the solute concentration is 1 part per million (ppm). \[\text{1 ppm}= \dfrac{\text{1 mg Solute}}{\text{1 L Solution}}\] The ppm unit can also be used in terms of volume/volume (v/v) instead (see example below).
- Parts per Billion: Parts per billion (ppb) is almost like ppm, except 1 ppb is 1000-fold more dilute than 1 ppm. \[\text{1 ppb} = \dfrac{1\; \mu \text{g Solute}}{\text{1 L Solution}}\]
- Parts per Trillion: Just like ppb, the idea behind parts per trillion (ppt) is similar to that of ppm. However, 1 ppt is 1000-fold more dilute than 1 ppb and 1000000-fold more dilute than 1 ppm. \[\text{1 ppt} = \dfrac{ \text{1 ng Solute}}{\text{1 L Solution}}\]
Here is a table with the volume percent of different gases found in air. Volume percent means that for 100 L of air, there are 78.084 L Nitrogen, 20.946 L Oxygen, 0.934 L Argon and so on; Volume percent mass is different from the composition by mass or composition by amount of moles.
| Elements Name | Volume Percent (v/v) | ppm (v/v) |
|---|---|---|
| Nitrogen | 78.084 | 780,840 |
| Oxygen | 20.946 | 209,460 |
| Water Vapor | 4.0% | 40,000 |
| Argon | 0.934 | 9,340 |
| Carbon Dioxide | 0.0379 | 379* (but growing rapidly) |
| Neon | 0.008 | 8.0 |
| Helium | 0.000524 | 5.24 |
| Methane | 0.00017 | 1.7 |
| Krypton | 0.000114 | 1.14 |
| Ozone | 0.000001 | 0.1 |
| Dinitrogen Monoxide | 0.00003 | 0.305 |
Concentration Units based on moles
- Mole Fraction: The mole fraction of a substance is the fraction of all of its molecules (or atoms) out of the total number of molecules (or atoms). It can also come in handy sometimes when dealing with the \(PV=nRT\) equation. \[\chi_A= \dfrac{\text{number of moles of substance A}}{\text{total number of moles in solution}}\] Also, keep in mind that the sum of each of the solution's substances' mole fractions equals 1. \[\chi_A + \chi_B + \chi_C \;+\; ... \;=1\]
- Mole Percent: The mole percent (of substance A) is \(\chi_A\) in percent form. \[\text{Mole percent (of substance A)}= \chi_A \times 100\%\]
- Molarity: The molarity (M) of a solution is used to represent the amount of moles of solute per liter of the solution. \[M= \dfrac{\text{Moles of Solute}}{\text{Liters of Solution}}\]
- Molality: The molality (m) of a solution is used to represent the amount of moles of solute per kilogram of the solvent. \[m= \dfrac{\text{Moles of Solute}}{\text{Kilograms of Solvent}}\]
The molarity and molality equations differ only from their denominators. However, this is a huge difference. As you may remember, volume varies with different temperatures. At higher temperatures, volumes of liquids increase, while at lower temperatures, volumes of liquids decrease. Therefore, molarities of solutions also vary at different temperatures. This creates an advantage for using molality over molarity. Using molalities rather than molarities for lab experiments would best keep the results within a closer range. Because volume is not a part of its equation, it makes molality independent of temperature.
In a solution, there is 111.0 mL (110.605 g) solvent and 5.24 mL (6.0508 g) solute present in a solution. Find the mass percent, volume percent and mass/volume percent of the solute.
Solution
Mass Percent
=(Mass of Solute) / (Mass of Solution) x 100%|
=(6.0508g) / (110.605g + 6.0508g) x 100%
=(0.0518688312) x 100%
=5.186883121%
Mass Percent= 5.186%
Volume Percent
=(Volume of Solute) / (Volume of Solution) x 100%
=(5.24mL) / (111.0mL + 5.24mL) x 100%
=(0.0450791466) x 100%
=4.507914659%
Volume Percent= 4.51%
Mass/Volume Percent
=(Mass of Solute) / (Volume of Solution) x 100%
=(6.0508g) / (111.0mL + 5.24mL) x 100%
=(0.0520) x 100%
=5.205%
Mass/Volume Percent= 5.2054%
With the solution shown in the picture below, find the mole percent of substance C.
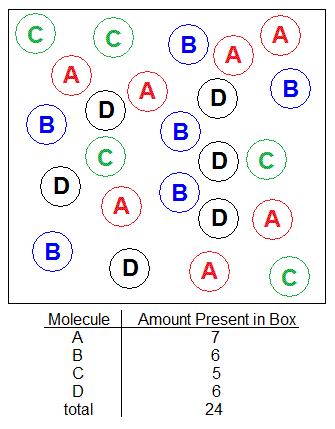
Solution
Moles of C= (5 C molecules) x (1mol C / 6.022x1023 C molecules) = 8.30288941x10-24mol C
Total Moles= (24 molecules) x (1mol / 6.022x1023 molecules)= 3.98538691x10-23mol total
XC= (8.30288941x10-24mol C) / (3.98538691x10-23mol) = .2083333333
Mole Percent of C
= XC x 100%
=(o.2083333333) x 100%
=20.83333333
Mole Percent of C = 20%
A 1.5L solution is composed of 0.25g NaCl dissolved in water. Find its molarity.
Solution
Moles of NaCl= (0.25g) / (22.99g + 35.45g) = 0.004277 mol NaCl
Molarity
=(Moles of Solute) / (Liters of Solution)
=(0.004277mol NaCl) / (1.5L)
=0.002851 M
Molarity= 0.0029M
0.88g NaCl is dissolved in 2.0L water. Find its molality.
Solution
Moles of NaCl= (0.88g) / (22.99g + 35.45g) = 0.01506 mol NaCl
Mass of water= (2.0L) x (1000mL / 1L) x (1g / 1mL) x (1kg / 1000g) = 2.0kg water
Molality
=(Moles of Solute) / (kg of Solvent)
=(0.01506 mol NaCl) / (2.0kg)
=0.0075290897m
Molality= 0.0075m
References
- Petrucci, Harwood, Herring. General Chemistry: Principles & Modern Applications. 8th ed. Upper Saddle River, New Jersey: Pearson/Prentice Hall, 2002. 528-531

