Raoult's Law
- Page ID
- 1598
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Raoult's law states that the vapor pressure of a solvent above a solution is equal to the vapor pressure of the pure solvent at the same temperature scaled by the mole fraction of the solvent present:
\[ P_{solution} = \chi_{solvent}P^o_{solvent} \label{RLaw} \]
Introduction
In the 1880s, French chemist François-Marie Raoult discovered that when a substance is dissolved in a solution, the vapor pressure of the solution will generally decrease. This observation depends on two variables:
- the mole fraction of the amount of dissolved solute present and
- the original vapor pressure (pure solvent).
At any given temperature for a particular solid or liquid, there is a pressure at which the vapor formed above the substance is in dynamic equilibrium with its liquid or solid form. This is the vapor pressure of the substance at that temperature. At equilibrium, the rate at which the solid or liquid evaporates is equal to the rate that the gas is condensing back to its original form. All solids and liquids have a vapor pressure, and this pressure is constant regardless of how much of the substance is present.
Ideal vs. Nonideal Solutions
Raoult's Law only works for ideal solutions. "An ideal solution shows thermodynamic mixing characteristics identical to those of ideal gas mixtures [except] ideal solutions have intermolecular interactions equal to those of the pure components."2 Like many other concepts explored in Chemistry, Raoult's Law only applies under ideal conditions in an ideal solution. However, it still works fairly well for the solvent in dilute solutions. In reality though, the decrease in vapor pressure will be greater than that calculated by Raoult's Law for extremely dilute solutions.3
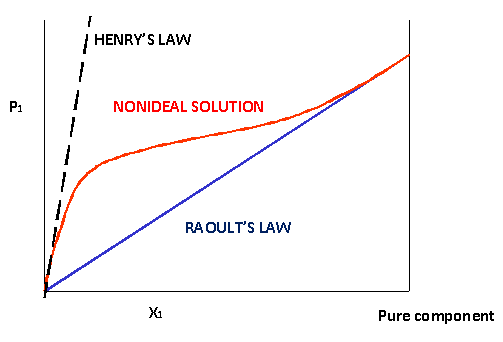
Why Raoult's Law works
If you look review the concepts of colligative properties, you will find that adding a solute lowers vapor pressure because the additional solute particles will fill the gaps between the solvent particles and take up space. This means less of the solvent will be on the surface and less will be able to break free to enter the gas phase, resulting in a lower vapor pressure. There are two ways of explaining why Raoult's Law works - a simple visual way, and a more sophisticated way based on entropy. Below is the simple approach.
Remember that saturated vapor pressure is what you get when a liquid is in a sealed container. An equilibrium is set up where the number of particles breaking away from the surface is exactly the same as the number sticking on to the surface again.
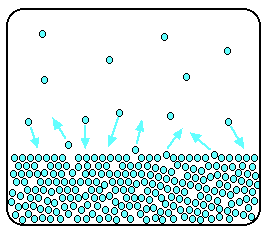
Now suppose solute molecules were added so that the solvent molecules occupied only 50% of the surface of the solution.

A certain fraction of the solvent molecules will have sufficient energy to escape from the surface (e.g., 1 in 1000 or 1 in a million). If you reduce the number of solvent molecules on the surface, you are going to reduce the number which can escape in any given time. But it will not make any difference to the ability of molecules in the vapor to stick to the surface again. If a solvent molecule in the vapor hits a bit of surface occupied by the solute particles, it may well stick. There are obviously attractions between solvent and solute otherwise you would not have a solution in the first place.
The net effect of this is that when equilibrium is established, there will be fewer solvent molecules in the vapor phase - it is less likely that they are going to break away, but there is not any problem about them returning. However, if there are fewer particles in the vapor at equilibrium, the saturated vapor pressure is lower.
Limitations on Raoult's Law
In practice, there's no such thing as an ideal solution! However, features of one include:
- Ideal solutions satisfy Raoult's Law. The solution in the last diagram of Figure \(\PageIndex{3}\) above would not actually obey Raoult's Law - it is far too concentrated, but was drawn so concentrated to emphasized the point.
- In an ideal solution, it takes exactly the same amount of energy for a solvent molecule to break away from the surface of the solution as it did in the pure solvent. The forces of attraction between solvent and solute are exactly the same as between the original solvent molecules - not a very likely event!

Suppose that in the pure solvent, 1 in 1000 molecules had enough energy to overcome the intermolecular forces and break away from the surface in any given time. In an ideal solution, that would still be exactly the same proportion. Fewer would, of course, break away because there are now fewer solvent molecules on the surface - but of those that are on the surface, the same proportion still break away. If there were strong solvent-solute attractions, this proportion may be reduced to 1 in 2000, or 1 in 5000 or whatever.
In any real solution of, say, a salt in water, there are strong attractions between the water molecules and the ions. That would tend to slow down the loss of water molecules from the surface. However, if the solution is sufficiently dilute, there will be good-sized regions on the surface where you still have water molecules on their own. The solution will then approach ideal behavior.
The nature of the solute
There is another thing that you have to be careful of if you are going to do any calculations on Raoult's Law. You may have noticed in the little calculation about mole fraction further up the page, that sugar was as a solute rather than salt. What matters is not actually the number of moles of substance that you put into the solution, but the number of moles of particles formed. For each mole of sodium chloride dissolved, you get 1 mole of sodium ions and 1 mole of chloride ions - in other words, you get twice the number of moles of particles as of original salt.
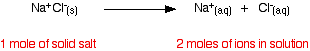
So, if you added 0.1 moles of sodium chloride, there would actually be 0.2 moles of particles in the solution - and that's the figure you would have to use in the mole fraction calculation. Unless you think carefully about it, Raoult's Law only works for solutes which do not change their nature when they dissolve. For example, they must not ionize or associate (e.g., if you put in substance A, it must not form A2 in solution). If it does either of these things, you have to treat Raoult's law with great care.
What matters is not actually the number of moles of substance that you put into the solution, but the number of moles of particles formed.
Raoult's Law and Colligative Properties
The effect of Raoult's Law is that the saturated vapor pressure of a solution is going to be lower than that of the pure solvent at any particular temperature. That has important effects on the phase diagram of the solvent. The next diagram shows the phase diagram for pure water in the region around its normal melting and boiling points. The 1 atmosphere line shows the conditions for measuring the normal melting and boiling points.
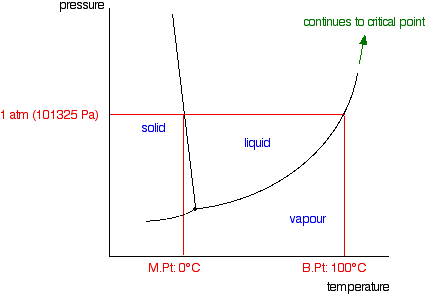
The line separating the liquid and vapor regions is the set of conditions where liquid and vapor are in equilibrium. It can be thought of as the effect of pressure on the boiling point of the water, but it is also the curve showing the effect of temperature on the saturated vapor pressure of the water. These two ways of looking at the same line are discussed briefly in a note about half-way down the page about phase diagrams (follow the last link above).
If you draw the saturated vapor pressure curve for a solution of a non-volatile solute in water, it will always be lower than the curve for the pure water.

If you look closely at the last diagram, you will see that the point at which the liquid-vapor equilibrium curve meets the solid-vapor curve has moved. That point is the triple point of the system - a unique set of temperature and pressure conditions at which it is possible to get solid, liquid and vapor all in equilibrium with each other at the same time. Since the triple point has solid-liquid equilibrium present (amongst other equilibria), it is also a melting point of the system - although not the normal melting point because the pressure is not one atmosphere.
The curves for the pure water and for the solution are often drawn parallel to each other. That has got to be wrong! Suppose you have a solution where the mole fraction of the water is 0.99 and the vapor pressure of the pure water at that temperature is 100 kPa. The vapor pressure of the solution will be 99 kPa - a fall of 1 kPa. At a lower temperature, where the vapor pressure of the pure water is 10 kPa, the fall will only be 0.1 kPa. For the curves to be parallel the falls would have to be the same over the whole temperature range. They aren't!
That must mean that the phase diagram needs a new melting point line (a solid-liquid equilibrium line) passing through the new triple point. That is shown in the next diagram.

Now we are finally in a position to see what effect a non-volatile solute has on the melting and freezing points of the solution. Look at what happens when you draw in the 1 atmosphere pressure line which lets you measure the melting and boiling points. The diagram also includes the melting and boiling points of the pure water from the original phase diagram for pure water (black lines).

Because of the changes to the phase diagram, you can see that:
- the boiling point of the solvent in a solution is higher than that of the pure solvent;
- the freezing point (melting point) of the solvent in a solution is lower than that of the pure solvent.
We have looked at this with water as the solvent, but using a different solvent would make no difference to the argument or the conclusions. The only difference is in the slope of the solid-liquid equilibrium lines. For most solvents, these slope forwards whereas the water line slopes backwards. You could prove to yourself that that does not affect what we have been looking at by re-drawing all these diagrams with the slope of that particular line changed. You will find it makes no difference whatsoever.
How to Calculate the Vapor Pressure of a Solution
We can calculate the vapor pressure of the solution in two ways, depending on the volatility of the solute. If the solute is volatile, it will exert its own vapor pressure and this amount is a significant contribution to the overall vapor pressure of the solution, and thus needs to be included in the calculations. On the other hand, if it is nonvolatile, the solute will not produce vapor pressure in solution at that temperature.
Nonvolatile solutes
These calculations are fairly straightforward if you are comfortable with stoichiometric conversions. Because the solute is nonvolatile, you need only determine the change in vapor pressure for the solvent. Using the equation for Raoult's Law, you will need to find the mole fraction of the solvent and the vapor pressure of the pure solvent is typically given.
1.5 moles of cherry Kool-Aid are added to a pitcher containing 2 liters of water on a nice day at 25o C. The vapor pressure of water alone is 23.8 mm Hg at 25o C. What is the new vapor pressure of Kool-Aid?
Solution
\(P_{H_2O}\) = 23.8 mm Hg
To solve for the mole fraction, you must first convert the 2 L of water into moles:
1 L = 1000 mL = 1000 g
Knowing this, you can convert the mass of water (2000 g) into moles:
2000 g / 18.02 g (molar mass of water) = 110.9 moles H2O
Solve for the mole fraction, \(\chi_{H_2O}\):
\(\chi_{H_2O}\) = moles H2O / total moles
= 110.9 moles / 110.9 + 1.5 moles = 0.979
Finally, apply Raoult's Law
\(P_{Kool-Aid} = \chi_{H_2O} \, P_{H_2O}\) = (0.979)(23.8 mm Hg) = 23.3 mm Hg
Calculate the vapor pressure of a solution made by dissolving 50.0 g glucose, \(C_6H_{12}O_6\), in 500 g of water. The vapor pressure of pure water is 47.1 torr at 37°C
Solution
To use Raoult's Law (Equation \(\ref{RLaw}\)), we need to calculate the mole fraction of water (the solvent) in this sugar-water solution.
\[ \chi_{solvent} = \dfrac{ \text{moles of water}}{\text{moles of solute} + \text{moles of solvent}} \nonumber \]
\[ \chi_{solvent} = \dfrac{ n_{water}}{ n_{glucose} + n_{water} } \nonumber\]
The molar mass of glucose if 180.2 g/mol and of water is 18 g/mol. So
\[n_{water} = \dfrac{500\,g}{18\,g /mol} = 27.7 \,mol \nonumber\]
and
\[n_{glucose} = \dfrac{50\,g}{180.2\,g /mol} = 0.277 \,mol \nonumber\]
and
\[ \chi_{solvent} = \dfrac{ 27.7 \,mol}{ 0.277 \,mol + 27.7 \,mol } = 0.99 \nonumber\]
Note that this still relatively dilute.
\[ P_{solution} = 0.99 \times 47.1 = 46.63 \, torr \nonumber\]
not much of a change at all.
Calculate the vapor pressure of a solution made by dissolving 50.0 g CaCl2, \(C_6H_{12}O_6\), in 500 g of water. The vapor pressure of pure water is 47.1 torr at 37°C
Solution
To use Raoult's Law (Equation \(\ref{RLaw}\)), we need to calculate the mole fraction of water (the solvent) in this salt-water solution.
\[ \chi_{solvent} = \dfrac{ \text{moles of water}}{\text{moles of solute} + \text{moles of solvent}} \nonumber\]
\[ \chi_{solvent} = \dfrac{ n_{water}}{ n_{solutes} + n_{water} } \nonumber\]
The molar mass of \(\ce{CaCl_2}\) if 111 g/mol and of water is 18 g/mol. So
\[n_{water} = \dfrac{500\,g}{18\,g /mol} = 27.7 \,mol \nonumber\]
and
\[n_{solutes} = \dfrac{50\,g}{111 \,g /mol} = 0.45 \,mol \nonumber\]
but this is really:
- \( n_{Ca^+} = 0.45 \,mol\)
- \( n_{Cl^-} = 0.9 \,mol\)
and
\[ \chi_{solvent} = \dfrac{ 27.7 \,mol}{ 0.45 \,mol + 0.9 \,mol + 27.7 \,mol } = 0.953 \nonumber\]
Note that this still relatively dilute.
\[ P_{solution} = 0.953 \times 47.1 = 44.88\, torr \nonumber\]
A bigger change that the glucose example above.
Volatile Solutes
The only difference between volatile and nonvolatile solutes, is that the partial pressure exerted by the vapor pressure of the volatile solute and the vapor pressure of the solvent must be accounted for. The sum of the two will give you the total vapor pressure of the solution.
What are the partial pressures of benzene and toluene in a solution in which the mole fraction of benzene is 0.6? What is the total vapor pressure? The vapor pressure of pure benzene is 95.1 mm Hg and the vapor pressure of pure toluene 28.4 mm Hg at 25oC.
Solution
If \(\chi_{benzene} = 0.6\), than \(\chi_{toluene} = 0.4\) because \(1 - 0.6 = 0.4\).
Now that we know the mole fractions and vapor pressures, this problem is a cinch.
Pbenzene = xbenzenePbenzene = (0.6)(95.1 mm Hg) = 57.1 mm Hg
Ptoluene = xtoluenePtoluene = (0.4)(28.4 mm Hg) = 11.4 mm Hg
The total vapor pressure is simply the sum of the partial pressures:
Ptotal = Pbenzene + Ptuolene = 57.1 mm Hg + 11.4 mm Hg = 68.5 mm Hg
Exercises
*MM = molar mass
- What is the vapor pressure of a solution at 25oC containing 78.0 grams of glucose (MM = 180.16 g/mol) in 500 grams of water? The vapor pressure of pure water at this temperature is 23.8 mm Hg.
- 25 grams of cyclohexane (Po = 80.5 torr, MM = 84.16 g/mol) and 30 grams of ethanol (Po = 52.3 torr, MM = 92.14 g/mol) are both volatile components present in a solution. What is the partial pressure of ethanol?
- What is the vapor pressure of pure butane at 20o C if its partial pressure is 698 mm Hg in a butane-acetone mixture where the mole fraction of acetone is x = 0.577?
Solution
1.
Solve for xH2O.
Moles H2O = 500 g / 18.02 g/mol = 27.7 moles H2O
Moles glucose = 78 g / 180.16 g/mol = 0.433 moles glucose
xH2O = 27.7 moles / (27.7 + 0.433) moles = 0.985
Now we can apply Raoult's Law.
\[P = XP^o = (0.985)(23.8\; mmHg) = 23.4\; mmHg\]
2.
Calculate the moles of each component.
- Moles cyclohexane: \(\dfrac{25\; g}{84.16\; g/mol} = 0.297 \; \text{moles of cyclohexane}\)
- Moles ethanol: \(\dfrac{30\; g}{92.14 \;g/mol} = 0.326 \; \text{moles ethanol}\)
Determine the mole fraction of ethanol and apply Raoult's Law.
Xethanol = 0.326 moles / (0.326 + 0.297) moles = 0.523
P = xPo = (0.523)(52.3 torr) = 27.4 torr
3.
If xacetone = 0.577 then xmethanol = 0.423 because 1 - 0.577 = 0.423
If you rearrange the Raoult's Law equation, you can solve for Po.
\[P = XP^o \rightarrow \]
\[P^o = \dfrac{P}{X} = \dfrac{698\; mmHg}{0.423} = 1650\; mmHg\]
References
- Petrucci, et al. General Chemistry Principles & Modern Applications. 9th ed. Upper Saddle River, NJ: Pearson Prentice Hall, 2007.
- Kugel, Roger W. "Raoult's Law: Binary Liquid-Vapor Phase Diagrams" Journal of Chemical Education 75.9 (1998): 1125.
- P. Tzias, C. Treiner, and M. Chemla. “Applicability of Raoult’s Law in Nonideal Mixed Solvents” Journal of Solution Chemistry 6.6 (1977): 393-402.

