6.1.7: The Collision Theory
- Page ID
- 3816
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page describes the collision theory of reaction rates, concentrating on the key factors that determine whether a particular collision will result in a reaction—in particular, the energy of the collision, and the orientation of the collision. Reactions in which a single species falls apart are simpler because the orientation of the molecule is unimportant. Reactions involving collisions between more than two species are extremely uncommon (see below).
Two species can only react with each other if they come into contact with each other and then they may react. However, it is not sufficient for the two species to just collide:
- they must collide the right way,
- and they must collide with enough energy for their chemical bonds to break.
The chances of this happening for more than two particles at a time are remote. All three (or more) particles would have to arrive at exactly the same point in space at the same time, with everything lined up exactly right, and with enough energy to react. Such circumstances are rarely observed in nature.
Requirement 1: The Orientation of Collision
Consider a simple reaction involving a collision between two molecules: for example, ethene, \(\ce{CH2=CH2}\), and hydrogen chloride, \(\ce{HCl}\). These react to give chloroethane as shown:
\[ \ce{H_2C=CH_2 + HCl \rightarrow CH_3CH_2Cl} \nonumber \]
As a result of the collision between the two molecules, the double bond in ethene is converted into a single bond. A hydrogen atom is now attached to one of the carbons and a chlorine atom to the other. The reaction can only happen if the hydrogen end of the \(\ce{H-Cl}\) bond approaches the carbon-carbon double bond. No other collision between the two molecules produces the same effect. The two simply bounce off each other.
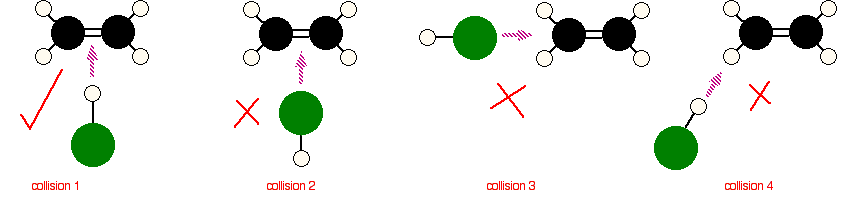
Of the collisions shown in Figure \(\PageIndex{2}\) only collision 1 may possibly lead on to a reaction. With no knowledge of the reaction mechanism, one might wonder why collision 2 would be unsuccessful. The double bond has a high concentration of negative charge around it due to the electrons in the bonds. The approaching chlorine atom is also partially negative due to dipole created by the electronegativity difference between it and hydrogen. The repulsion simply causes the molecules to bounce off each other. In any collision involving unsymmetrical species, the way they hit each other is important in determining whether a reaction occurs.
Requirement 2: Activation Energy
Even if the species are orientated properly, a reaction will not take place unless the particles collide with a certain minimum energy called the activation energy of the reaction. Activation energy is the minimum energy required to make a reaction occur. This can be illustrated on an energy profile for the reaction. An energy profile for a simple exothermic reaction is given in Figure \(\PageIndex{2}\).
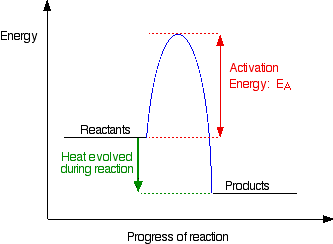
If the particles collide with less energy than the activation energy, nothing interesting happens. They bounce apart. The activation energy can be thought of as a barrier to the reaction. Only those collisions with energies equal to or greater than the activation energy result in a reaction.
Any chemical reaction results in the breaking of some bonds (which requires energy) and the formation of new ones (which releases energy). Some bonds must be broken before new ones can be formed. Activation energy is involved in breaking some of the original bonds. If a collision is relatively gentle, there is insufficient energy available to initiate the bond-breaking process, and thus the particles do not react.
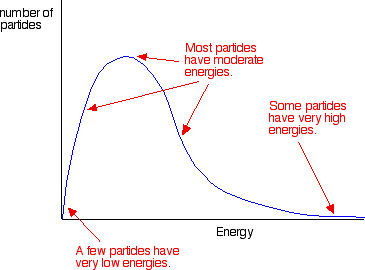
Because of the key role of activation energy in deciding whether a collision will result in a reaction, it is useful to know the proportion of the particles present with high enough energies to react when they collide. In any system, the particles present will have a very wide range of energies. For gases, this can be shown in Figure \(\PageIndex{3}\) and is called the Maxwell-Boltzmann distribution, a plot showing the number of particles with each particular energy.
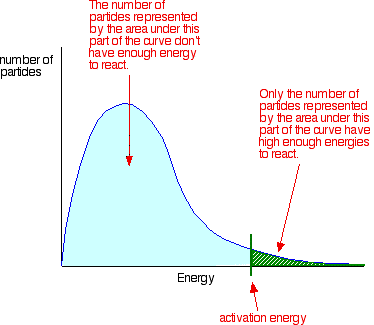
The area under the curve measures of the total number of particles present. Remember that for a reaction to occur, particles must collide with energies equal to or greater than the activation energy for the reaction. The activation energy is marked on the Maxwell-Boltzmann distribution with a green line. Notice that the large majority of the particles have insufficient energy to react when they collide. To enable them to react, either the shape of the curve must be altered, or the activation energy shifted further to the left. This is described on other pages.


