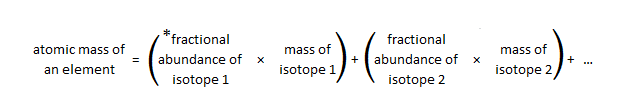Isotopes
- Page ID
- 1327
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Atoms that have the same atomic number (number of protons), but different mass numbers (number of protons and neutrons) are called isotopes. There are naturally occurring isotopes and isotopes that are artificially produced. Isotopes are separated through mass spectrometry; MS traces show the relative abundance of isotopes vs. mass number (mass : charge ratio).
Introduction
As mentioned before, isotopes are atoms that have the same atomic number, but different mass numbers. Isotopes are denoted the same way as nuclides, but they are often symbolized only with the mass numbers because isotopes of the same element have the the same atomic number. Carbon, for example, has two naturally occurring isotopes, \(^{12}_6C\) and \(^{13}_6C\). Because both of these isotopes have 6 protons, they are often written as \(^{12}C\) and \(^{13}C\). \(^{12}C\) has 6 neutrons, and \(^{13}C\) has 7 neutrons.
Of all the elements on the periodic table, only 21 are pure elements. Pure, or monotopic, elements are those elements with only one naturally occurring nuclide. The following lists the 21 pure elements:
- \(^{27}_{13}Al\)
- \(^{75}_{33}As\)
- \(^{9}_4Be\)
- \(^{209}_{83}Bi\)
- \(^{133}_{55}Cs\)
- \(^{59}_{27}Co\)
- \(^{19}_9F\)
- \(^{197}_{79}Au\)
- \(^{165}_{67}Ho\)
- \(^{127}_{53}I\)
- \(^{55}_{25}Mn\)
- \(^{93}_{41}Nb\)
- \(^{31}_{15}P\)
- \(^{141}_{59}Pr\)
- \(^{103}_{45}Rh\)
- \(^{45}_{21}Sc\)
- \(^{23}_{11}Na\)
- \(^{159}_{65}Tb\)
- \(^{232}_{90}Th\)
- \(^{169}_{69}Tm\)
- \(^{89}_{39}Y\)
Isotopes of the other elements either occur naturally or are artificially produced.
Natural and Artificial Isotopes
Most elements have naturally occurring isotopes. Percent natural abundances indicate which isotopes of any given element are predominant (occur in greater abundance) and which only occur in trace amounts. Mercury, for example, has seven naturally occurring isotopes: \(^{196}Hg\), \(^{198}Hg\), \(^{199}Hg\), \(^{200}Hg\), \(^{201}Hg\), \(^{202}Hg\), \(^{204}Hg\); these have the percent natural abundances of 0.146%, 10.02%, 16.84%, 23.13%, 13.22%, 29.80%, and 6.85%, respectively. It is clear that \(^{202}Hg\) occurs with greatest abundance, and \(^{200}Hg\) is the next most abundant, but the other isotopes only occur in small traces.
Note: The sum of the percent natural abundances of all the isotopes of any given element must total 100%.
There are 20 elements with only artificially produced isotopes. The majority of these are heavier elements; the lightest elements with artificial isotopes are \(^{43}Tc\) and \(^{61}Pm\). The other elements that only have artificial isotopes are those with atomic numbers of 84-88 and 89-103, otherwise known as the actinoids, but excluding \(^{90}Th\) and \(^{92}U\).
Some naturally occurring and artificially produced isotopes are radioactive. The nucleus of a radioactive isotope is unstable; radioactive isotopes spontaneously decay, emitting alpha, beta, and gamma rays until they reach a stability, usually in the state of a different element. Bismuth (\(^{209}_{83}Bi\)) has the highest atomic and mass number of all the stable nuclides. All nuclides with atomic number and mass number greater than 83 and 209, respectively, are radioactive. However, there are some lighter nuclides that are radioactive. For example, hydrogen has two naturally occurring stable isotopes, \(^{1}H\) and \(^{2}H\) (deuterium), and a third naturally occurring radioactive isotope, \(^{3}H\) (tritium).
Radioisotope Dating
The presence of certain radioisotopes in an object can be used to determine its age. Carbon dating is based on the fact that living plants absorb stable \(^{12}C\), \(^{13}C\) and radioactive \(^{14}C\) from the atmosphere, and animals absorb them from the plants. An organism no longer absorbs carbon after it dies, its age can be determined by measuring the ratio of \(^{13}C\) to \(^{14}C\) in the sample and extrapolating based on its decay rate.
Art forgeries are often detected by similar means. \(^{137}Cs\) and \(^{90}Sr\) do not occur naturally and are only present in the atmosphere today because of nuclear weapons. Any object created before July 1945, then, would have neither of these elements, so finding them through mass spectrometry or other means would indicate that it was created later.
Isotopic Masses, Percent Natural Abundance, and Weighted-Average Atomic Mass
Because most elements occur as isotopes and different isotopes have different masses, the atomic mass of an element is the average of the isotopic masses, weighted according to their naturally occurring abundances; this is the mass of each element recorded on the periodic table, also known as the relative atomic mass (Ar). Treating isotopic masses in weighted averages gives greater importance to the isotope with greatest percent natural abundance. Below is a general equation to calculate the atomic mass of an element based on percent natural abundance and isotopic masses:
* fractional abundance is the percent abundance divided by 100%
Bromine has two naturally occurring isotopes: bromine-79 has a mass of 78.9183 u and an abundance of 50.69%, and bromine-81 has a mass of 80.92 u and an abundance of 49.31%. The equation above can be used to solve for the relative atomic mass of bromine:
atomic mass of Br = (0.5069 x 78.9183 u) + (0.4931 x 80.92 u) = 79.91 u
This is the relative atomic number of bromine that is listed on the periodic table.
Comparing their isotopic masses of any given element to the relative atomic mass of the element reveals that the Ar is very close to the isotope that occurs most frequently. Thus, the isotope whose isotopic mass is closest to the atomic mass of the element is the isotope that occurs in the greatest abundance.
Mass Spectrometry
Mass spectrometry is a technique that can be used to distinguish between isotopes of a given element. A mass spectrometer separates each isotope by mass number. Each isotope is characterized by a peak (of given intensity) according to its relative abundance. The most intense peak corresponds to the isotope that occurs in the largest relative natural abundance, and vice versa. Refer to Mass Spectrometry: Isotope Effects.
Example:
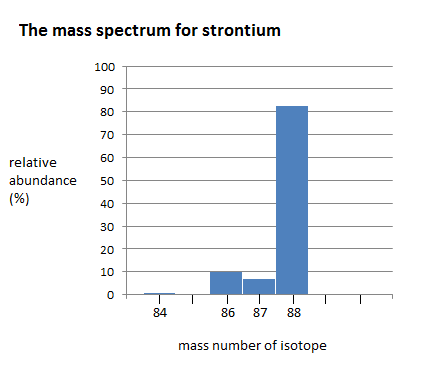
The mass spectrum of strontium has four different peaks, varying in intensity. The four peaks indicate that there are four isotopes of strontium. The four isotopes of strontium have isotopic mass numbers of 84, 86, 87, and 88, and relative abundances of 0.56%, 9.86%, 7.00%, and 82.58%, respectively. The intensity of the peak corresponds to the abundance. \(^{84}Sr\) has the smallest peak, which corresponds to its relative abundance of 0.56%, whereas \(^{88}Sr\) has the largest peak, which corresponds to its relative abundance of 82.58%. This indicates that \(^{88}Sr\) is the isotope that occurs in highest amounts.
References
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, and Jeffry D. Madura. General Chemistry: Principles and Modern Application. Ninth ed. New Jersey: Pearson Prentice Hall, 2007.
- Housecraft, Catherine E. and Alan G. Sharpe. Inorganic Chemistry. Third ed. England: Pearson Prentice Hall, 2008.
- Hoefs, Jochen. Stable Isotope Geochemistry. Sixth ed. Germany: Springer, 2009.
Problems
1) Find the number of protons and neutrons in the following isotopes: a) \(^{20}Ne\), \(^{21}Ne\), \(^{22}Ne\); b) \(^{84}Sr\), \(^{86}Sr\), \(^{87}Sr\), \(^{88}Sr\); c) \(^{102}Pd\), \(^{104}Pd\), \(^{105}Pd\), \(^{106}Pd\), \(^{108}Pd\), \(^{110}Pd\)
(Answer: a) \(^{20}Ne\) has 10 p and 10 n; \(^{21}Ne\) has 10 p and 11 n; \(^{22}Ne\) has 10 p and 12 n; b) \(^{84}Sr\) has 38 p and 46 n, \(^{86}Sr\) has 38 p and 48 n, \(^{87}Sr\) has 38 p and 49 n, \(^{88}Sr\) has 38 p and 50 n; c) \(^{102}Pd\) has 46 p and 56 n, \(^{104}Pd\) has 46 p and 58 n, \(^{105}Pd\) has 46 p and 59 n, \(^{106}Pd\) has 46 p and 60 n, \(^{108}Pd\) has 46 p and 62 n, \(^{110}Pd\) has 46 p and 64 n)
2) An isotope of lead has an isotopic mass of 208. Give the appropriate notation for the isotope.
(Answer: \(^{208}Pb\))
3) Thallium has two naturally occurring istotopes, \(^{203}Tl\) and \(^{205}Tl\). Tl-205 has an abundance of 70.48%. What is the percent natural abundance of Tl-203?
(Answer: 29.52%)
4) Chlorine has two naturally occuring isotopes, \(^{35}Cl\) and \(^{37}Cl\), with masses of 34.97 u and 36.97 u, respectively. Which of these two isotopes occur in greater abundance?
(Answer: \(^{35}Cl\))
5. Potassium has three naturally occurring isotopes: \(^{39}K\), \(^{40}K\), and \(^{41}K\), with masses (and abundances) of 38.96 u (93.3%), 39.96 u (0.012%), and 40.96 u (6.7%), respectively. Calculate the relative atomic mass of K.
(Answer: 39.10 u)
Review Questions
- What do the terms 'monotopic' and 'radioactive' mean?
- On the mass spectrum of any given atom, what does the number and intensity of the peak(s) tell you?
- What is the relationship between isotopic masses, percent natural abundance, and weighted-average atomic mass?