Ionization Energies of Diatomic Molecule
- Page ID
- 10975
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The energies of electrons in molecular orbitals can be observed directly by measuring the ionization energy. This is the energy required to remove an electron, in this case, from a molecule:
\[H_2 (g) \rightarrow H_2^+(g) + e^-(g)\]
The measured ionization energy of H2 is 1488 kJ mol-1. This number is primarily important in comparison to the ionization energy of a hydrogen atom, which is 1312 kJ mol-1. Therefore, it requires more energy to remove an electron from the hydrogen molecule than from the hydrogen atom; the electron therefore has a lower energy in the molecule. To pull the atoms apart, the energy of the electron must be increased. Hence, energy is required to break the bond, and the molecule is bound.
A bond is formed when the energy of the electrons in the molecule is lower than the energy of the electrons in the separated atoms. This conclusion is consistent with the view of shared electrons in bonding molecular orbitals.
As a second example, consider the nitrogen molecule, \(N_2\). The ionization energy of molecular nitrogen is 1503 kJ mol-1, and that of atomic nitrogen is 1402 kJ mol-1. Once again, the energy of the electrons in molecular nitrogen is lower than that of the electrons in the separated atoms, so the molecule is bound.
As a third example, consider fluorine, \(F_2\). In this case, find that the ionization energy of molecular fluorine is 1515 kJ mol-1, which is smaller than the ionization energy of a fluorine atom, 1681 kJ mol-1. This seems inconsistent with the bonding orbital concept developed above, which states that the electrons in the bond have a lower energy than in the separated atoms. If the electron being ionized has a higher energy in \(F_2\) than in F, why is \(F_2\) a stable molecule? A more complete description of the molecular orbital concept of chemical bonding is required.
Bond energies are next considered. Recall that the bond energy (or bond strength) is the energy required to separate the bonded atoms. The bond energy of \(N_2\) is 956 kJ mol-1; this is much larger than the bond energy of H2, 458 kJ mol-1, and of \(F_2\), which is 160 kJ mol-1. The unusually strong bond in nitrogen can be explained using both the valence shell electron pair sharing model and electron orbital descriptions. A nitrogen atom has three unpaired electrons in its valence shell; the three 2p electrons distribute themselves over the three 2p orbitals, each oriented along a different axis. Each of these unpaired electrons is available for sharing with a second nitrogen atom. The result, from valence shell electron pair sharing concepts, is that three pairs of electrons are shared between two nitrogen atoms in a “triple bond.” Intuition suggests that the triple bond in \(N_2\) should be much stronger than the single bond in H2 or in \(F_2\).
Now consider the molecular orbital description of bonding in \(N_2\). Each of the three 2p atomic orbitals in each nitrogen atom must overlap to form a bonding molecular orbital, to accommodate three electron pairs. Each 2p orbital is oriented along a single axis. One 2p orbital from each atom is oriented in the direction of the other atom, that is, along the bond axis. When these two atomic orbitals overlap, they form a molecular orbital with cylindrical symmetry and is therefore a σ orbital (a σ* orbital is also formed). The two electrons are paired in the bonding orbital.
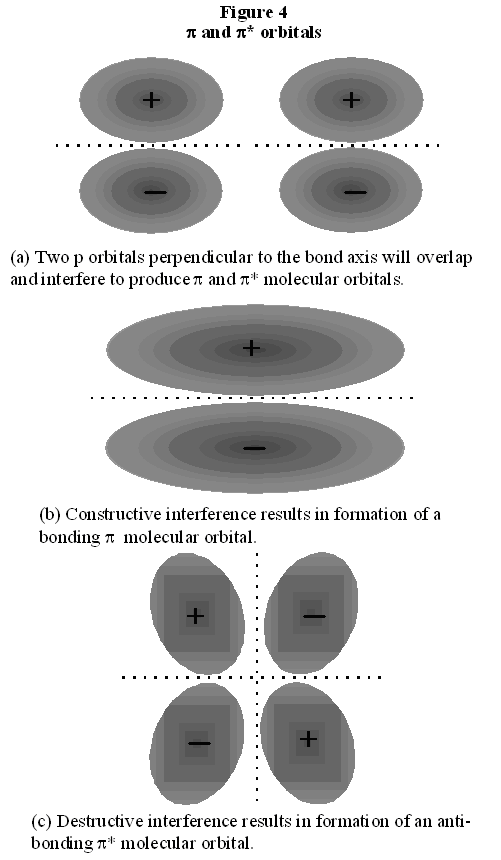
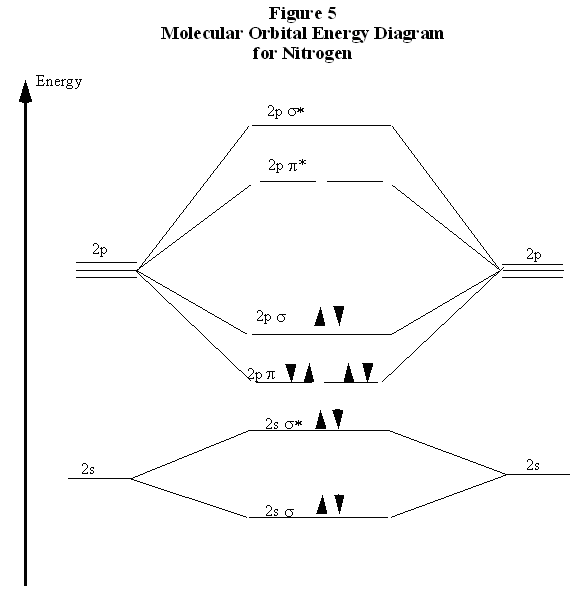
This effect is depicted in Fig. 5 in a molecular orbital energy diagram. Each pair of atomic orbitals, one from each atom, overlaps to form a bonding and an anti-bonding orbital. The three 2p orbitals from each atom form one σ and σ* pair and two π and π* pairs. The lowering of the energies of the electrons in the σand π orbitals is apparent. The ten n=2 electrons from the nitrogen atoms are then placed pairwise, in order of increasing energy, into these molecular orbitals. Note that, in agreement with the Pauli Exclusion Principle, each pair in a single orbital consists of one spin up and one spin down electron.
Recall now that the discussion of bonding was begun with \(N_2\) because of the curious result that the ionization energy of an electron in \(F_2\) is less than that of an electron in an F atom. Comparing the molecular orbital energy level diagrams for \(N_2\) and \(F_2\) allows an explanation for this puzzle. There are five p electrons in each fluorine atom. These ten electrons must be distributed over the molecular orbitals whose energies are shown in Fig. 6. (Note that the ordering of the bonding 2p orbitals differ between \(N_2\) and \(F_2\).) Two electrons are placed in the σ orbital, four more in the two π orbitals, and four more in the two π* orbitals. Overall, there are six electrons in bonding orbitals and four in anti-bonding orbitals. Because \(F_2\) is a stable molecule, we must conclude that the lowering of energy for the electrons in the bonding orbitals is greater than the raising of energy for the electrons in the antibonding orbitals. Overall, this distribution of electrons is, net, equivalent to having two electrons paired in a single bonding orbital.
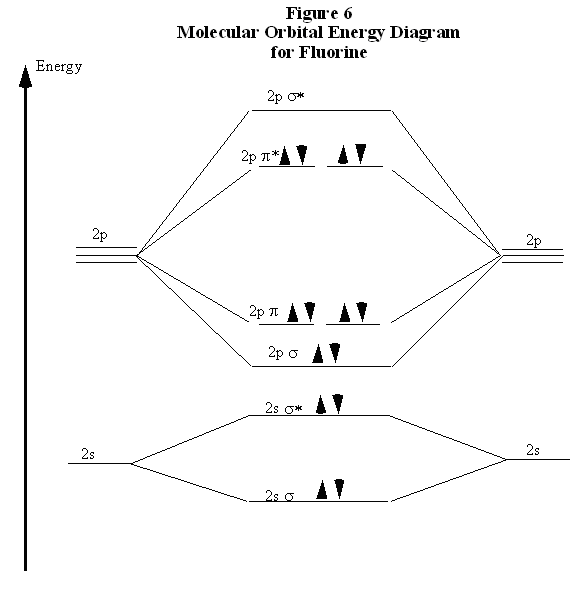
This also explains why the ionization energy of \(F_2\) is less than that of an F atom. The electron with the highest energy requires the least energy to remove from the molecule or atom. The molecular orbital energy diagram in Fig. 6 clearly shows that the highest energy electrons in \(F_2\) are in anti-bonding orbitals. Therefore, one of these electrons is easier to remove than an electron in an atomic 2p orbital, because the energy of an antibonding orbital is higher than that of the atomic orbitals, and the system is stabilized by the electron's removal. Therefore, the ionization energy of molecular fluorine is less than that of atomic fluorine. This clearly demonstrates the physical reality and importance of the antibonding orbitals.
A particularly interesting case is the oxygen molecule, \(O_2\). In completing the molecular orbital energy level diagram for oxygen, the last two electrons must either be paired in the same 2p π* orbital or separated into different 2p π* orbitals. To determine which, it is important to note that oxygen molecules are paramagnetic—they are strongly attracted to a magnetic field. To account for this paramagnetism, recall that electron spin is a magnetic property. In most molecules, all electrons are paired, so for each “spin up” electron there is a “spin down” electron and their magnetic fields cancel out. If all electrons are paired, the molecule is diamagnetic, meaning that it responds only weakly to a magnetic field.
If the electrons are not paired, they can adopt the same spin in the presence of a magnetic field. This accounts for the attraction of the paramagnetic molecule to the magnetic field. Therefore, for a molecule to be paramagnetic, it must have unpaired electrons. The correct molecular orbital energy level diagram for an \(O_2\) molecule is shown in Fig. 7.
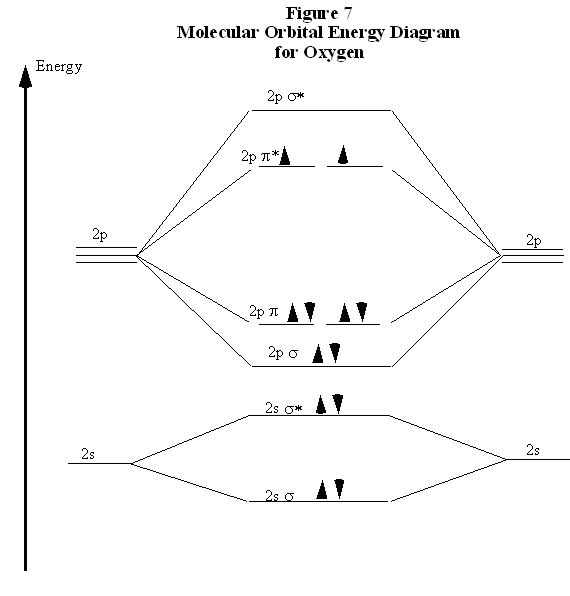
In comparing these three diatomic molecules, recall that \(N_2\) has the strongest bond, followed by \(O_2\) and \(F_2\). The comparative bond strengths were previously accounted for with Lewis structures, showing that \(N_2\) is a triple bond, \(O_2\) is a double bond, and \(F_2\) is a single bond. The molecular orbital energy level diagrams in Figs. 5 to 7 add more perspective to this analysis. Note that, in each case, the number of bonding electrons in these molecules is eight. The difference in bonding is entirely due to the number of antibonding electrons: 2 for \(N_2\), 4 for \(O_2\), and six for \(F_2\). Thus, the strength of a bond must be related to the relative numbers of bonding and antibonding electrons in the molecule. Therefore, the bond order is defined as the following:
\[\text{Bond order} = \frac{1}{2} (\# \ of\ bonding\ electrons - \# \ of\ antibonding\ electrons) \]
Note that, defined this way, the bond order for \(N_2\) is 3, for \(O_2\) is 2, and for \(F_2\) is 1, which agrees with the conclusions made from Lewis structures. In conclusion, the relative strengths of bond can be predicted by comparing bond orders.

