8.48: Another Bell Theorem Analysis - Shorter Version

The purpose of this tutorial is to review Jim Baggott's analysis of Bell's theorem as presented in Chapter 4 of The Meaning of Quantum Theory using matrix and tensor algebra.

A two-stage atomic cascade emits entangled photons (A and B) in opposite directions with the same circular polarization according to observers in their path.

\[ | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ |L \rangle_A |L \rangle_B + |R \rangle_A | R \rangle_B \right] \nonumber \]

The experiment involves the measurement of photon polarization states in the vertical/horizontal measurement basis, and allows for the rotation of the right-hand detector through an angle of θ, in order to explore the consequences of quantum mechanical entanglement. PA stands for polarization analyzer and could simply be a calcite crystal.

In vector notation the left- and right- circular polarization states are expressed as follows:

Left circular polarization:

\[ L = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ i \end{pmatrix} \nonumber \]

Right circular polarization:

\[ R = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ -i \end{pmatrix} \nonumber \]

In tensor notation the initial state is the following entangled superposition,

\[ | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ | L \rangle_A | L \rangle_B + |R \rangle_A | R \rangle_B \right] = \frac{1}{ 2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ i \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ i \end{pmatrix}_B + \begin{pmatrix} 1 \\ -i \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ -i \end{pmatrix}_B \right] = \frac{1}{2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ i \\ i \\ -1 \end{pmatrix} + \begin{pmatrix} 1 \\ -i \\ -i \\ -1 \end{pmatrix} \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} \nonumber \]

However, as mentioned above, the photon polarization measurements will actually be made in the vertical/horizontal basis. These polarization measurement states for photons A and B in vector representation are given below. Θ is the angle through which the PA2 has been rotated.

Vertical polarization:

\[ \begin{matrix} V_A = \begin{pmatrix} 1 \\ 0 \end{pmatrix} & V_B = \begin{pmatrix} \cos \theta \\ \sin \theta \end{pmatrix} \end{matrix} \nonumber \]

Horizontal polarization:

\[ \begin{matrix} V_A = \begin{pmatrix} 0 \\ 1 \end{pmatrix} & V_B = \begin{pmatrix} \sin \theta \\ \cos \theta \end{pmatrix} \end{matrix} \nonumber \]

It is easy to show that |Ψ> in the vertical/horizontal basis is,

\[ | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ | V \rangle_A | V \rangle_B + |H \rangle_A |H \rangle_B \right] = \frac{1}{ 2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix}_B + \begin{pmatrix} 0 \\ 1 \end{pmatrix}_A \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix}_B \right] = \frac{1}{2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \\ 0 \\ 0 \end{pmatrix} + \begin{pmatrix} 0 \\ 0 \\ 0 \\ 1 \end{pmatrix} \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} \nonumber \]

A joint measurement operator is created using the A and B photon measurement eigenstates, with vertical polarization assigned an eigenvalue of +1 and horizontal polarization an eigenvalue of -1. This operator is then used to calculate the expectation value or correlation function.

\[ \begin{matrix} V_A V_A^T - H_A H_A^T \rightarrow \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} & V_B V_B^T - H_B H_B^T \text{simplify} \rightarrow \begin{pmatrix} \cos ( 2 \theta) & - \sin (2 \theta) \\ - \sin (2 \theta) & 2 \sin ( \theta)^2 -1 \end{pmatrix} \end{matrix} \nonumber \]

\[ \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \otimes \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} = \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) & 0 & 0 \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 & 0 & 0 \\ 0 & 0 & - \cos (2 \theta) & \sin (2 \theta) \\ 0 & 0 & \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} \nonumber \]

\[ \begin{matrix} \Psi = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} & E( \theta) = \Psi \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) & 0 & 0 \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 & 0 & 0 \\ 0 & 0 & - \cos (2 \theta) & \sin (2 \theta) \\ 0 & 0 & \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} \Psi \text{simplify} \rightarrow \cos (2 \theta) \end{matrix} \nonumber \]

As shown above the evaluation of E(θ) yields cos(2θ). For θ = 0⁰ there is perfect correlation; for θ = 90⁰ perfect anti-correlation; for θ = 45⁰ no correlation.

\[ \begin{matrix} E \text{(0 deg)} = 1 & E \text{(90 deg)} = -1 & E \text{(45 deg)} = 0 \end{matrix} \nonumber \]

Baggott presented a correlation function for this experiment based on a local hidden variable model of reality (pp. 110-113, 127-131). It (linear blue line) and the quantum mechanical correlation function, E(θ), are compared on the graph below. Quantum theory and local realism disagree at all angles except 0, 45 and 90 degrees.

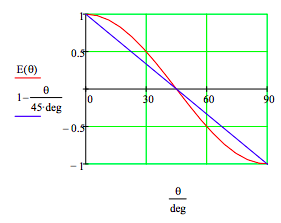
This example illustrates Bell's theorem: no local hidden-variable theory can reproduce all the predictions of quantum mechanics for entangled composite systems. As the quantum predictions are confirmed experimentally, the local hidden-variable approach to reality must be abandoned.

In spite of the correlation shown in the joint polarization measurements, the individual measurements on photons 1 and 2 are totally random for all values of θ, i.e. E(θ) = 0. For example, the following operator is used to calculate the expectation value for measurements on photon 2 as a function of its analyzer's angle θ. The identity operator represents no measurement on spin 1.

\[ \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \otimes \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} = \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) & 0 & 0 \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 & 0 & 0 \\ 0 & 0 & - \cos (2 \theta) & \sin (2 \theta) \\ 0 & 0 & \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} \nonumber \]

\[ E( \theta) = \Psi^T \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} = \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) & 0 & 0 \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 & 0 & 0 \\ 0 & 0 & - \cos (2 \theta) & \sin (2 \theta) \\ 0 & 0 & \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} \nonumber \]

Naturally the same is true for photon 1.

\[ \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) \\ - \sin (2 \theta) & 2 \sin^2 ( \theta) - 1 \end{pmatrix} \otimes \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} = \begin{pmatrix} \cos (2 \theta) & 0 & - \sin (2 \theta) & 0 \\ 0 & \cos (2 \theta) & 0 & - \sin (2 \theta) \\ - \sin (2 \theta) & 0 & 2 \sin^2 ( \theta) -1 \\ 0 & - \sin (2 \theta) & 0 & 2 \sin^2 ( \theta) - 1 \end{pmatrix} \Psi ~ \text{simplify} \rightarrow 0 \nonumber \]

The expectation value calculations can also be performed using the trace function as shown below.

\[ \langle \Psi | \hat{O} | \Psi \rangle = \sum_i \langle \Psi | \hat{O} | i \rangle \langle i | \Psi \rangle = \sum_i \langle i | \Psi \rangle \langle \Psi | \hat{O} | i \rangle = Trace \left( | \Psi \rangle \langle \Psi | \hat{O} \right) ~ \text{where} ~ \sum_i |i \rangle \langle i | = \text{Identity} \nonumber \]

\[ tr \begin{bmatrix} \Psi \Psi^T \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) & 0 & 0 \\ - \sin (2 \theta) & 2 \sin ( \theta)^2 - 1 & 0 & 0 \\ 0 & 0 & - \cos(2 \theta) & \sin (2 \theta) \\ 0 & 0 & \sin (2 \theta) & 1 - 2 \sin ( \theta)^2 \end{pmatrix} \end{bmatrix} ~ \text{simplify} \rightarrow ~ \cos ( 2 \theta) \nonumber \]

\[ tr \left[ \Psi ~ \Psi^T \begin{pmatrix} \cos (2 \theta) & - \sin (2 \theta) & 0 & 0 \\ - \sin (2 \theta) & 2 \sin( \theta)^2 - 1 & 0 & 0 \\ 0 & 0 & - \cos (2 \theta) & \sin (2 \theta) \\ 0 & 0 & \sin (2 \theta) & 1 - 2 \sin ( \theta)^2 \end{pmatrix} \right] ~ \text{simplify}~ \rightarrow \cos (2 \theta) \nonumber \]