8.46: Jim Baggott's Bell Theorem Analysis

The purpose of this tutorial is to review Jim Baggott's analysis of Bell's theorem as presented in Chapter 4 of The Meaning of Quantum Theory using matrix and tensor algebra.

A two-stage atomic cascade emits entangled photons (A and B) in opposite directions with the same circular polarization according to the observers in their path.

\[ \begin{matrix} | \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ | L \rangle_A | L \rangle_B + |R \rangle_A | R \rangle_B \right] = \frac{1}{ 2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ i \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ i \end{pmatrix}_B + \begin{pmatrix} 1 \\ -i \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ -i \end{pmatrix}_B \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} & \Psi = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} \end{matrix} \nonumber \]

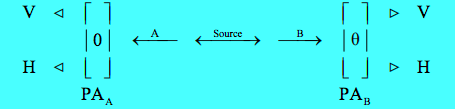
The experiment involves the measurement of photon polarization states in the vertical/horizontal measurement basis using calcite crystals, and allows that the polarization analyzers (PAs) can be oriented at different angles a and b. The figure below is taken from Chapter 4 of Jim Baggott's The Meaning of Quantum Theory.

The equivalent wave function in the vertical/horizontal basis is:

\[| \Psi \rangle = \frac{1}{ \sqrt{2}} \left[ | V \rangle_A | V \rangle_B - |H \rangle_A | H \rangle_B \right] = \frac{1}{ 2 \sqrt{2}} \left[ \begin{pmatrix} 1 \\ 0 \end{pmatrix}_A \otimes \begin{pmatrix} 1 \\ 0 \end{pmatrix}_B + \begin{pmatrix} 0 \\ 1 \end{pmatrix}_A \otimes \begin{pmatrix} 0 \\ 1 \end{pmatrix}_B \right] = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} \nonumber \]

The matrix operator representing the calcite crystal, where θ is the angle of rotation of the crystal relative to the vertical is:

\[ \begin{matrix} \text{Calcite}( \theta) = \begin{pmatrix} \cos (2 \theta) & \sin (2 \theta) \\ \sin (2 \theta) & - \cos (2 \theta) \end{pmatrix} & \text{Calcite(0)} = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} & \text{Calcite} \left( \frac{ \pi}{4} \right) = \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} & \text{Calcite} \left( \frac{ \pi}{2} \right) = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} \end{matrix} \nonumber \]

The eigenvalues of the calcite operator for any orientation angle are +/- 1. Several examples are shown below.

\[ \begin{matrix} \text{eigenvals(Calcite(0))} = \begin{pmatrix} 1 \\ -1 \end{pmatrix} & \text{eigenvals} \left( \text{Calcite} \left( \frac{ \pi}{4} \right) \right) = \begin{pmatrix} 1 \\ -1 \end{pmatrix} & \text{eigenvals} \left( \text{Calcite} \left( \frac{ \pi}{6} \right) \right) = \begin{pmatrix} 1 \\ -1 \end{pmatrix} \end{matrix} \nonumber \]

The eigenvalue +1 is assigned to the vertical transmission channel and the -1 eigenvalue to the horizontal transmission channel.

Since only the relative angle between the two PAs is important, PA₁ is held at the vertical orientation (θ = 0) and PA₂ is rotated. The operator for this experimental set-up is as follows.

\[ Rot( \theta) \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} \otimes \begin{pmatrix} \cos ( 2 \theta) & \sin (2 \theta) \\ \sin (2 \theta) & - \cos (2 \theta) \end{pmatrix} = \begin{pmatrix} \cos (2 \theta) & \sin (2 \theta) & 0 & 0 \\ \sin (2 \theta) & - \cos (2 \theta) & 0 & 0 \\ 0 & 0 & - \cos(2 \theta) & - \sin (2 \theta) \\ 0 & 0 & - \sin (2 \theta) & \cos (2 \theta) \end{pmatrix} \nonumber \]

The expectation value of the Rot(θ) operator is a measure of the correlation between the joint measurements.

\[ E( \theta) = \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 & 0 & 0 & -1 \end{pmatrix} \begin{pmatrix} \cos (2 \theta) & \sin (2 \theta) & 0 & 0 \\ \sin (2 \theta) & - \cos (2 \theta) & 0 & 0 \\ 0 & 0 & - \cos(2 \theta) & - \sin (2 \theta) \\ 0 & 0 & - \sin (2 \theta) & \cos (2 \theta) \end{pmatrix} \frac{1}{ \sqrt{2}} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} ~ \text{simplify} ~ \rightarrow \cos (2 \theta) \nonumber \]

As shown above evaluation of E(θ) yields cos(2θ). For θ = 0⁰ there is perfect correlation; for θ = 90⁰ perfect anti-correlation; for θ = 45⁰ no correlation.

\[ \begin{matrix} E \text{(0 deg)} = 1 & E \text{(90 deg)} = -1 & E \text{(45 deg)} = 0 \end{matrix} \nonumber \]

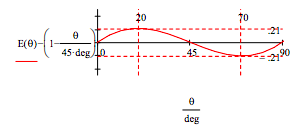
Baggott derived a correlation function for this experiment based on a local hidden variable model of reality (pp. 110-113, 127-131). It (linear blue line) and the quantum mechanical correlation function, E(θ), are compared on the graph below. Quantum theory and local realism disagree at all angles except 0, 45 and 90 degrees.

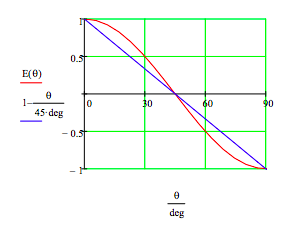
Maximum disagreement between quantum theory and the local hidden variable model occurs at 20 and 70 degrees.