7.8: Illustrating the Superposition Principle with Single Photon Interference
- Page ID
- 137888
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Abstract
Single-photon interference in a Mach-Zehnder interferometer is used to illustrate the superposition principle. Three methods of analysis of an historically important experiment are presented at a level appropriate for an undergraduate course in quantum chemistry or physics. The importance of the superposition principle in chemistry is also discussed.
Introduction
Introducing the double-slit experiment as paradigmatic of the bizarre nature of quantum mechanical behavior, Richard Feynman wrote,
We choose to examine a phenomenon which is impossible, absolutely impossible, to explain in any classical way, and which has in it the heart of quantum mechanics. In reality, it contains the only mystery. We cannot make the mystery go away by “explaining” how it works. We will just tell you how it works. In telling you how it works we will have told you about the basic peculiarities of all quantum mechanics.(1)
Amplifying the last sentence of this quotation Feynman said the double-slit experiment is so fundamental that if asked a question about quantum mechanics one can always reply, “You remember the case of the experiment with the two holes? It’s the same thing.”(2) The crucial point being made is that the double-slit experiment is the simplest manifestation of the ubiquitous superposition principle and its attendant interference effects. The superposition principle, according to Feynman, permeates quantum mechanics, and is the origin of the strangeness we associate with quantum mechanical phenomena.
Having identified the mystery and conceptual difficulty of quantum mechanics Feynman went on to point out that computationally it was frequently quite simple.
We have come to the conclusion that what are usually called the advanced parts of quantum mechanics are, in fact, quite simple. The mathematics that is involved is particularly simple, involving simple algebraic operations and no differential equations or at most very simple ones. (3)
Single-Photon Interference
Recently Scarani and Suarez (4) illustrated this mathematical simplicity by providing an elementary quantum mechanical analysis of an historically important experiment (5) that is a close relative of the famous double-slit experiment. Fig. 1 shows a schematic diagram of an equal-arm Mach-Zehnder interferometer consisting of two 50-50 beam splitters and two mirrors. The experiment is run at low source intensity such that there is only one photon in the interferometer at a time.
Three idealized experiments are considered for pedagogical purposes. (I) If either path is blocked 50% of the photons get through, and 25% reach D1 and 25% reach D2. (II) In the absence of the second beam splitter (BS2) 50% of the time the photon is detected at D1 and 50% of the time it is detected at D2. (III) However, in the presence of BS2 the photon is always detected at D1 and never at D2. Three methods will be used to analyze the surprising result of experiment III. Of course the key will be that in this experiment each detector can be reached by two paths, whereas in experiments I and II there is only one path to each detector.
First Method
We will begin with a brief review of the analysis given by Scarani and Suarez for experiment III before presenting two alternative approaches. After the first beam splitter the photon is in an even linear superposition of being transmitted \( |T \rangle \) and reflected \( |R \rangle\).
\[ |S \rangle \rightarrow \frac{1}{ \sqrt{2}} \big[ |T \rangle + i |R \rangle \big] \nonumber \]
By convention a \( \frac{ \pi}{2}\) (i) phase shift is assigned to the reflected beam. More will be said about this below.
The mirrors (6) direct the two beams to the second beam splitter where, according to the superposition principle, \( |T \rangle \) and \( |R \rangle\) evolve as follows,
\[ |T \rangle \rightarrow \frac{1}{ \sqrt{2}} \big[ i|D_1 \rangle + |D_2 \rangle \big] \nonumber \]
\[ |R \rangle \rightarrow \frac{1}{ \sqrt{2}} \big[ |D_1 \rangle + i|D_2 \rangle \big] \nonumber \]
where again the \( \frac{ \pi}{2}\) phase shift is assigned to the reflection. Substitution of eqns (2) and (3) into (1) yields
\[ |S \rangle \rightarrow i |D_1 \rangle \nonumber \]
Thus, the probability that the photon will arrive at D1 is
\[ \big| \langle D_1 |S \rangle \big|^2 = 1 \nonumber \]
It is easy to show that if there is no phase difference between reflection and transmission 1 2 (i.e. replace i by 1 in equations (1), (2), and (3)) the probabilities for arrival at D1 and D2 are both 1. This is a clear violation of energy conservation because one photon has become two photons with no mechanism for a reduction of energy of the individual photons. Thus, conservation of energy is a compelling argument for a \( \frac{ \pi}{2}\) phase difference between transmission and reflection.
Second Method
The second method uses Dirac notation to enumerate the probability amplitudes for arrival at the two detectors. As in the above analysis, at the beam splitters the probability amplitude for transmission is \( \frac{1}{ \sqrt{2}}\), and for reflection it is \( \frac{i}{ \sqrt{2}}\). Because the photon path is not observed the probability is calculated as the square of the absolute magnitude of the sum of the probability amplitudes for each path. Thus, the probability amplitudes for the two paths may interfere constructively and destructively. As shown below the probability amplitudes to reach D1 are in phase (TR+RT) and those to reach D2 are 180° out of phase (TT+RR), so the photon is never detected at D2.
\[ \big| \langle D_1 |S \rangle \big|^2 = \big| \langle D_1 |T \rangle \langle T |S \rangle + \langle D_1 |R \rangle \langle R|S \rangle \big|^2 = \bigg| \frac{i}{ \sqrt{2}} \frac{1}{ \sqrt{2}} + \frac{1}{ \sqrt{2}} \frac{i}{ \sqrt{2}} \bigg|^2 = 1 \nonumber \]
\[ \big| \langle D_2 |S \rangle \big|^2 = \big| \langle D_2 |T \rangle \langle T |S \rangle + \langle D_2 |R \rangle \langle R|S \rangle \big|^2 = \bigg| \frac{1}{ \sqrt{2}} \frac{1}{ \sqrt{2}} + \frac{i}{ \sqrt{2}} \frac{i}{ \sqrt{2}} \bigg|^2 = 0 \nonumber \]
While it is customary to refer to this experiment as an example of single-particle interference, Glauber (7) recommends more careful language.
The things that interfere in quantum mechanics are not particles. They are probability amplitudes for certain events. It is the fact that probability amplitudes add up like complex numbers that is responsible for all quantum mechanical interferences.
What Glauber is saying here is clearly revealed in this second method of analysis.
Third Method
The third method illustrates how the experiment is analyzed using matrix mechanics.(8) In this approach the photon’s translational states \( |x \rangle \) (horizontal) and \( |y \rangle \) (vertical) are represented by the orthonormal basis vectors shown below.
\[ |x \rangle = \begin{pmatrix}
1\\
0
\end{pmatrix} ~~~ |y \rangle = \begin{pmatrix}
0\\
1
\end{pmatrix} ~~~ \langle x | = \begin{pmatrix}
1 & 0
\end{pmatrix} ~~~ \langle y| = \begin{pmatrix}
0 & 1
\end{pmatrix} \nonumber \]
The operators for the interaction of the photon with a 50-50 beam splitter and a mirror (6) are represented by the following matrices.
\[ BS = \frac{1}{ \sqrt{2}} \begin{pmatrix}
1 & i\\
i & 1
\end{pmatrix} ~~~ M = \begin{pmatrix}
0 & 1\\
1 & 0
\end{pmatrix} \nonumber \]
To be detected at D1 a photon must be in the translational state \( |x \rangle\) after interacting with two beam splitters and a mirror in the configuration shown in Fig. 1. To be detected at D2 it must be in the translational state \( |y \rangle \). The probabilities for these outcomes are calculated using equations (8) and (9) as follows:
\[ \big| \langle x |BS (M) BS | x \rangle \big|^2 = 1 ~~~ \big| \langle y |BS (M) BS | x \rangle \big|^2 = 0 \nonumber \]
It is easy to confirm the rest by hand calculation.
Recapitulation
Dirac emphasized the unique role of the superposition principle in his seminal treatise on quantum mechanics by saying, “There is an entirely new idea involved, to which one must get accustomed and in terms of which one must proceed to build up an exact mathematical theory, without having any detailed classical picture.”(9)
The best way to get accustomed to the ubiquitous, but non-classical nature of the quantum mechanical superposition is through the study of those phenomena where it reveals itself most directly. Single-photon interference in a Mach-Zehnder interferometer provides a very simple example of the superposition principle in action, and is therefore suitable for presentation to undergraduates studying quantum chemistry or quantum physics. The same is true, of course, for the more widely known double-slit experiment.
The Superposition Principle in Chemistry
Having introduced the superposition with three analyses of an experiment in quantum optics, we will now briefly review its importance in chemistry. The superposition principle informs the chemists view of atomic and molecular structure, and is especially important in unifying the many facets of chemical bonding (10).
For example, an electronic wave function, whether atomic or molecular, is a weighted linear superposition. In atoms and molecules...
Electrons are characterized by their entire distributions (called wave functions or orbitals) rather than by instantaneous positions and velocities: an electron may be considered always to be (with appropriate probability) at all points of its distribution (which does not vary with time). (11)
Electrons confined in atoms and molecules are not moving in a classical sense; if they were they would radiate energy continuously, and atomic and molecular stability would be raised to the status of a scientific miracle. Atomic and molecular electrons are not here and later there, rather they are, at the same time, here and there. Just as the photon is present simultaneously in both arms of the Mach-Zehnder interferometer, the electron is present at all possible locations (properly weighted) in atoms and molecules. The confined electron is in an atomic or molecular stationary state.
Similar arguments pertain to molecular vibrations (12) and rotations. In the absence of external perturbations, such as electromagnetic radiation, molecules do not really vibrate and rotate about their centers of mass for the same reason electrons do not orbit the nucleus; such behavior would lead to the continuous emission of electromagnetic radiation, and again call into question the stability of matter. In the nanoscopic world of atoms and molecules motion only occurs during transitions from one stationary state to another – during the so called quantum jump.
The superposition principle also provides a viable model for this quantum jump, the transition between quantized stationary states, which is the essential process in all forms of spectroscopy. (13) Under the influence of an electromagnetic perturbation, a molecule or atom in an initial stationary state may move into a time-dependent linear superposition of the initial state and some final state.
\[ \Psi (r, t) = c_i (t) \Psi _i (r, t) exp \left( - \frac{iE_i t}{ \hbar} \right) + c_f (t) \Psi _f (r, t) exp \left( - \frac{iE_f t}{ \hbar} \right) \nonumber \]
If the Bohr frequency condition is met, \( v = \frac{E_f - E_i}{h}\), and \( | \Psi (r, t)|^2\) exhibits oscillating electric dipole character, the transition may occur, otherwise it is forbidden. In summary, the superposition principle provides an interpretation of quantized stationary states and the transitions between them induced by electromagnetic radiation.
Conclusion
Feynman has identified the superposition principle as the fundamental mystery of quantum mechanics. Accepting this view is good pedagogy, because it helps us teachers to see the coherence of this strange and awesome subject, and hopefully to pass that vision on to our students. It is characteristic of great thinkers, like Feynman, that they see the threads that make the tapestry.
Literature cited
1. Feynman, R. P.; Leighton, R. B.; Sands, M., The Feynman Lectures on Physics, Vol. 3; Addison-Wesley: Reading, 1965, p. 1-1.
2. Feynman, R. P. The Character of Physical Law; MIT Press: Cambridge, 1967; p. 130.
3. Feynman, R. P.; Leighton, R. B.; Sands, M., The Feynman Lectures on Physics, Vol. 3; Addison-Wesley: Reading, 1965, p. 3-1.
4. Scarani, V.; Suarez, A. “Introducing quantum mechanics: One-particle interferences,” Am. J. Phys. 1998, 66, 718-721.
5. Grangier, P.; G. Roger, G.; Aspect, A. “Experimental Evidence for Photon Anticorrelation Effects on a Beam Splitter: A New Light on Single-Photon Interferences,” Europhys. Lett 1986, 1, 173-179.
6. The \( \frac{ \pi}{2}\) phase shift accompanying reflection at the mirrors can be ignored because there are mirrors in both arms of the interferometer.
7. Glauber, R. J. “Dirac’s famous dictum,” Am. J. Phys. 1995, 63, 12.
8. This suggestion was made to the author by V. Scarani in a private communication.
9. Dirac, P. A. M. Principles of Quantum Mechanics, 4th ed.; Oxford U. P.: London, 1958, p.12.
10. Weinhold, F. A. “Chemical Bonding as a Superposition Phenomenon,” J. Chem. Educ. 1999, 76, 1141-1146.
11. Harris, F. E. “Molecules,” The Encyclopedia of Physics, 2nd ed.; R. G. Lerner, Ed. New York, VCH Publishers, 1990, p. 763.
12. Baskin, J. S.; Zewail, A. H. “Freezing Atoms in Motion: Principles of Femtochemistry and Demonstration by Laser Stroboscopy,” J. Chem. Educ. 2001, 78, 737-751.
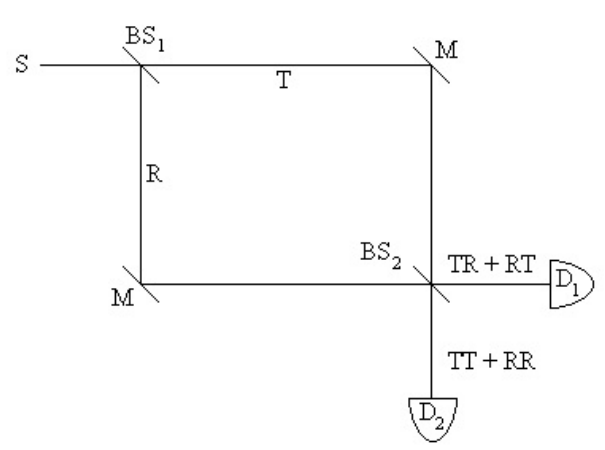
Fig. 1 Schematic diagram of a Mach-Zehnder interferometer. S = source; BS = beam splitter; M = mirror 1 ; R = reflected; T = transmitted; D = detector; TT = transmitted at BS and 2 1 2 transmitted at BS ; TR = transmitted at BS and reflected at BS ; etc.

