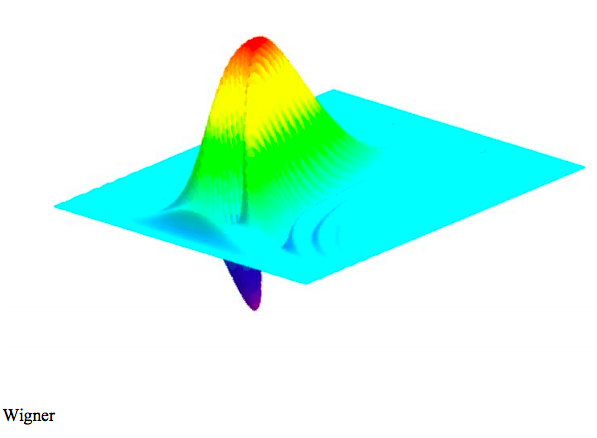
2.59: The Wigner Distribution for the 3p State of the 1D Hydrogen Atom
- Page ID
- 158673
This tutorial presents three pictures of the 3p state of the one‐dimensional hydrogen atom using its position, momentum and phase‐space representations.
The energy operator for the one‐dimensional hydrogen atom in atomic units is:
\[ \frac{-1}{2} \frac{d^2}{dx^2} \blacksquare + \frac{ \text{L(L+1)}}{2x^2} \blacksquare - \frac{1}{x} \blacksquare \nonumber \]
The 3p wave function is:
\[ \begin{matrix} \Psi (x) = \frac{8}{27 \sqrt{6}} \left( 1 - \frac{x}{6} \right) x^2 \text{exp} \left( \frac{-x}{2} \right) & \int_0^{ \infty} \Psi (x)^2 dx = 1 \end{matrix} \nonumber \]
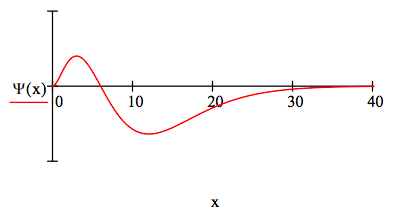
The 3p state energy is ‐0.0556 Eh.
\[ \frac{-1}{2} \frac{d^2}{dx^2} \Psi (x) + \frac{1}{x^2} \Psi (x) - \frac{1}{x} \Psi (x) = \text{E} \Psi (x) \text{ solve, E} \rightarrow \frac{-1}{18} = -0.0556 \nonumber \]
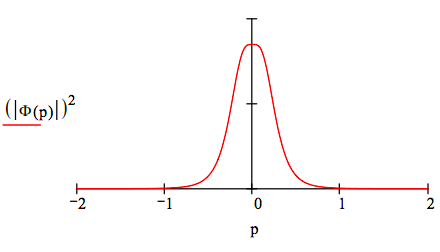
The momentum wave function is generated by the following Fourier transform of the coordinate space wave function.
\[ \Phi (p) = \frac{1}{ \sqrt{2 \pi}} \int_0^{ \infty} \text{exp(-i p x)} \Psi (x) dx \rightarrow \frac{2}{3} 2^{ \frac{1}{2}} 6^{ \frac{1}{2}} \frac{(-1) + 6 \text{i p}}{(3 \text{i p} +1)^4 \pi^{ \frac{1}{2}}} \nonumber \]
The Wigner function (phase‐space representation) for the 3p state is generated using the momentum wave function.
\[ \text{W(x, p)} = \frac{1}{2 \pi} \int_{- \infty}^{ \infty} \overline{ \Phi \left( \text{p} + \frac{ \text{s}}{2} \right)} \text{exp(-i s x)} \Phi \left( \text{p} - \frac{ \text{s}}{2} \right) \text{ds} \nonumber \]
The Wigner distribution is displayed graphically.
\[ \begin{matrix} N = 150 & i = 0 .. N & x_i = \frac{35i}{N} & j = 0 .. N & p_j = -2 + \frac{4j}{N} & \text{Wigner}_{i,~j} = \text{W} \left( x_i,~p_j \right) \end{matrix} \nonumber \]
