2.30: Atomic Variational Calculations- Hydrogen to Boron
- Page ID
- 156472
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The purpose of this tutorial is to calculate the ground-state energies of simple multi-electron atoms and ions using the variational method. In the interest of mathematical and computational simplicity the single parameter, orthonormal hydrogenic wave functions shown below will be used. The method will be illustrated for boron, but can be used for any atomic or ionic species with five or less electrons.
Using the following orthonormal trial wave functions, the various contributions to the total electronic energy of a multi-electron atom are given below in terms of the variational parameter, α. For further detail see: "Atomic Variational Calculations: Hydrogen to Boron," The Chemical Educator 1999, 4, 40-43. It should be pointed out that in these calculations the exchange interaction is ignored. Including exchange generally improves the results by about 1%.
\[ \begin{matrix} \Psi_{1s} \left( \alpha,~ \text{r} \right) = \sqrt{ \frac{ \alpha^3}{ \pi}} \text{exp} \left( - \alpha,~ \text{r} \right) & \Psi_{2s} \left( \alpha,~ \text{r} \right) = \sqrt{ \frac{ \alpha^3}{32 \pi}} (2 - \alpha \text{r}) \text{exp} \left( \frac{- \alpha r}{2} \right) & \Psi_{2p} \left( \alpha,~ r,~ \theta \right) = \sqrt{ \frac{ \alpha^3}{32 \pi}} \alpha \text{r exp} \left( \frac{ - \alpha \text{r}}{2} \right) \cos ( \theta) \end{matrix} \nonumber \]
The method will be illustrated with boron which has the electronic structure 1s22s22p1.
Nuclear charge: Z = 5
Seed value for variational parameter α: α = Z
Kinetic energy integrals:
\[ \begin{matrix} T_{1s} ( \alpha ) = \frac{ \alpha^2}{2} & T_{2s} ( \alpha ) = \frac{ \alpha^2}{8} & T_{2p} ( \alpha ) = \frac{ \alpha^2}{8} \end{matrix} \nonumber \]
Electron-nucleus potential energy integrals:
\[ \begin{matrix} V_{N1s} ( \alpha ) = -Z \alpha & V_{N2s} ( \alpha ) = - \frac{Z}{4} \alpha & V_{N2p} ( \alpha ) = - \frac{Z}{4} \alpha \end{matrix} \nonumber \]
Electron-electron potential energy integrals:
\[ \begin{matrix} V_{1s1s} ( \alpha ) = \frac{5}{8} \alpha & V_{1s2s} ( \alpha ) = \frac{17}{81} \alpha & V_{1s2p} ( \alpha ) = \frac{59}{243} \alpha & V_{2s2s} ( \alpha ) = \frac{77}{512} \alpha & V_{2s2p} ( \alpha ) = \frac{83}{512} \alpha \end{matrix} \nonumber \]
Enter coefficients for each contribution to the total energy:
\[ \begin{matrix} T_{1s} & T_{2s} & T_{2p} & V_{N1s} & V_{N2s} & V_{N2p} & V_{1s1s} & V_{1s2s} & V_{1s2p} & V_{2s2s} & V_{2s2p} \\ \colorbox{yellow}{a = 2} & \colorbox{yellow}{b = 2} & \colorbox{yellow}{c = 1} & \colorbox{yellow}{d = 2} & \colorbox{yellow}{e = 2} & \colorbox{yellow}{f = 1} & \colorbox{yellow}{g = 1} & \colorbox{yellow}{h = 4} & \colorbox{yellow}{i = 2} & \colorbox{yellow}{j = 1} & \colorbox{yellow}{k = 2} \end{matrix} \nonumber \]
Variational energy equation:
\[ \begin{matrix} E ( \alpha ) = & \text{a} T_{1s} ( \alpha ) + \text{b} T_{2s} ( \alpha ) + \text{c} T_{2p} ( \alpha ) + \text{d} V_{N1s} ( \alpha ) + \text{e} V_{n2s} ( \alpha ) + \text{f} V_{N2p} ( \alpha ) ... \\ \text{g} V_{1s1s} ( \alpha ) + \text{h} V_{1s2s} ( \alpha ) + \text{i} V_{1s2s} ( \alpha ) + \text{j} V_{2s2s} ( \alpha ) + \text{k} V_{2s2p} ( \alpha ) \end{matrix} \nonumber \]
Minimize energy with respect to the variational parameter, α.
\[ \begin{matrix} \alpha = \text{Minimize} \left( E,~ \alpha \right) & \alpha = 4.118 & E ( \alpha ) = -23.320 \end{matrix} \nonumber \]
The experimental ground state energy is the negative of the sum of the successive ionization energies of the atom or ion (see table of experimental data below):
\[ \begin{matrix} \text{SumIE} = 0.305 + 0.926 + 1.395 + 9.527 + 12.500 & E_{exp} = \text{SumIE} & E_{exp} = -24.653 \end{matrix} \nonumber \]
Compare theory and experiment:
\[ \begin{vmatrix} \frac{E ( \alpha ) - E_{exp}}{E_{exp}} \end{vmatrix} = 5.405 \% \nonumber \]
Calculate orbital energies of a 1s, 2s and 2p electron by filling the place holders with the appropriate coefficients (0, 1, 2, ...). Compare the calculated results with experimental values (see table below):
\[ \begin{matrix} \begin{array}{l l} E_{1s} ( \alpha) = & 1 T_{1s} ( \alpha ) + 0 T_{2s} ( \alpha ) + 0 T_{2p} ( \alpha ) + 1 V_{N1s} ( \alpha ) ... \\ & + 0 V_{N2s} ( \alpha ) + 0 V_{N2p} ( \alpha ) + 1 V_{1s1s} ( \alpha ) + 2 V_{1s2s} ( \alpha ) ... \\ & + 1 V_{1s2p} ( \alpha ) + 0 V_{2s2s} ( \alpha ) + 0 V_{2s2p} ( \alpha ) \end{array} & E_{1s} ( \alpha ) = -6.809 & \text{Exp} = -7.355 \\ \begin{array}{l l} E_{2s} ( \alpha) = & 0 T_{1s} ( \alpha ) + 1 T_{2s} ( \alpha ) + 0 T_{2p} ( \alpha ) + 0 V_{N1s} ( \alpha ) ... \\ & + 1 V_{N2s} ( \alpha ) + 0 V_{N2p} ( \alpha ) + 0 V_{1s1s} ( \alpha ) + 2 V_{1s2s} ( \alpha ) ... \\ & + 0 V_{1s2p} ( \alpha ) + 1 V_{2s2s} ( \alpha ) + 1 V_{2s2p} ( \alpha ) \end{array} & E_{2s} ( \alpha ) = -0.012 & \text{Exp} = -0.518 \\ \begin{array}{l l} E_{1s} ( \alpha) = & 0 T_{1s} ( \alpha ) + 0 T_{2s} ( \alpha ) + 1 T_{2p} ( \alpha ) + 0 V_{N1s} ( \alpha ) ... \\ & + 0 V_{N2s} ( \alpha ) + 1 V_{N2p} ( \alpha ) + 0 V_{1s1s} ( \alpha ) + 0 V_{1s2s} ( \alpha ) ... \\ & + 2 V_{1s2p} ( \alpha ) + 0 V_{2s2s} ( \alpha ) + 2 V_{2s2p} ( \alpha ) \end{array} & E_{2p} ( \alpha ) = 0.307 & \text{Exp} = -0.305 \end{matrix} \nonumber \]
\[ \begin{matrix} \text{Successive Ionization Energies for the First Six Elements} & \text{Orbital Energies for the First Six Atoms} \\ \begin{pmatrix} \text{Element} & \text{IE}_1 & \text{IE}_2 & \text{IE}_3 & \text{IE}_4 & \text{IE}_5 & \text{IE}_6 \\ \text{H} & 0.500 & \text{x} & \text{x} & \text{x} & \text{x} & \text{x} \\ \text{He} & 0.904 & 2.000 & \text{x} & \text{x} & \text{x} & \text{x} \\ \text{Li} & 0.198 & 2.782 & 4.500 & \text{x} & \text{x} & \text{x} \\ \text{Be} & 0.343 & 0.670 & 5.659 & 8.000 & \text{x} & \text{x} \\ \text{B} & 0.305 & 0.926 & 1.395 & 9.527 & 12.500 & \text{x} \\ \text{C} & 0.414 & 0.896 & 1.761 & 2.370 & 14.482 & 18.000 \end{pmatrix} & \begin{pmatrix} \text{Element} & 1s & 2s & 2p \\ \text{H} & -0.500 & \text{x} & \text{x} \\ \text{He} & -0.904 & \text{x} & \text{x} \\ \text{Li} & -2.386 & -0.198 & \text{x} \\ \text{Be} & -4.383 & -0.343 & \text{x} \\ \text{B} & -7.355 & -0.518 & -0.305 \\ \text{C} & -10.899 & -0.655 & -0.414 \end{pmatrix} \end{matrix} \nonumber \]
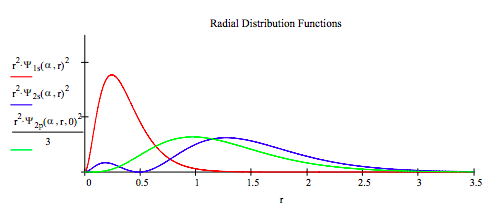
Interpretation of results:
With this model for atomic structure we are able to compare theory with experiment in two ways. The calculated ground-state energy is compared to the negative of the sum of the successive ionization energies. This comparison shows that theory is in error by 5.4% - not bad for a one-parameter model for a five-electron atom.
However, the comparison of the calculated orbital energies with the negative of the orbital ionization energies is not so favorable. It is clear that the one-parameter model used in this calculation does not do a very good job on the valence electrons. For example, the 2s electrons are barely bound and the 2p electron is not bound at all.
The total energy (ground-state energy) comparison is more favorable because the model does a decent job on the non-valence electrons where the vast majority of the energy resides. Chemistry, however, is dictated by the behavior of the valence electrons, so the failure of the model to calculate good orbital energies, and therefore good wave functions, for the valence electrons is a serious problem. This is a common problem in atomic and molecular calculations; finding wave functions that effectively model the behavior of both the core and the valence electrons.
Suggested additional problems: H, H-, Li, Li+, Be, C+, and Li atom excited state 1s22p1.

