2.15: Quantum Mechanical Calculations for the Hydrogen Atom
- Page ID
- 155169
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Full kinetic energy operator in spherical coordinates:
Kinetic energy operator for s states:
\[ - \frac{1}{2r} \frac{d^2}{dr^2} \blacksquare \nonumber \]
Kinetic energy operator for p states:
\[ \begin{matrix} - \frac{1}{2r} \frac{d^2}{dr^2} r \blacksquare ... \\ + \frac{-1}{2r^2 \sin ( \theta )} \left[ \frac{d}{d \theta} \left( \sin ( \theta ) \frac{d}{d \theta} \blacksquare \right) \right] ... \\ + \frac{-1}{2r^2 \sin ( \theta)^2} \frac{d^2}{d \phi^2} \blacksquare \end{matrix} \nonumber \]
Position operator: r
Potential energy operator: \( - \frac{1}{r}\)
Triple integral with volume element: \( \int_0^{ \infty} \int_0^{ \pi} \int_0^{ 2 \pi} \blacksquare r^2 \sin ( \theta ) d \phi d \theta dr\)
Orbitals:
\[ \begin{matrix} \Psi_{1s} (r) = \frac{1}{ \sqrt{ \pi}} \text{exp(-r)} & \Psi_{2s} (r) = \frac{1}{ \sqrt{32 \pi}} (2 - r) \text{exp} \left( - \frac{r}{2} \right) \\ \Psi_{2pz} (r,~ \theta) = \frac{1}{ \sqrt{32 \pi}} \text{r exp} \left( - \frac{r}{2} \right) \cos \theta & \Psi_{2py} (r,~ \theta,~ \phi ) = \frac{1}{ \sqrt{32 \pi}} \text{r exp} \left( - \frac{r}{2} \right) \sin ( \theta ) \sin ( \phi ) \end{matrix} \nonumber \]
Plot the wave functions on the same graph:
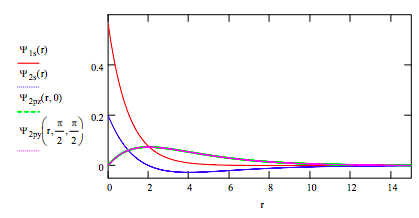
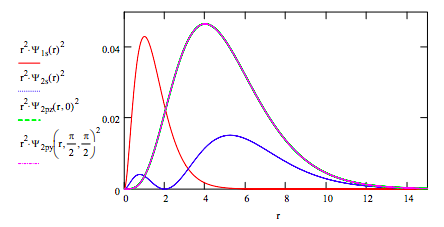
Plot the radial distribution functions for each orbital on the same graph:
Demonstrate that the 1s orbital is normalized:
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{1s} (r)^2 r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 1 \nonumber \]
Demonstrate that the 1s orbital is normalized:
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2s} (r)^2 r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 1 \nonumber \]
Demonstrate that the 2pz orbital is normalized:
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2pz} (r,~ \theta)^2 r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 1 \nonumber \]
Demonstrate that the 1s and the 2pz orbitals are orthogonal:
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{1s}(r) \Psi_{2pz} (r,~ \theta)^2 r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 0 \nonumber \]
Demonstrate the 1s and 2s orbitals are orthogonal:
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{1s}(r) \Psi_{2s} (r)^2 r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 0 \nonumber \]
Demonstrate that the 2py and the 2pz orbitals are orthogonal:
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2py} (r,~ \theta,~ \phi ) \Psi_{2pz} (r,~ \theta ) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 0 \nonumber \]
Determine the most probable value for r using the Trace function and calculus:
\[ \frac{d}{dr} r^2 \Psi_{1s}(r)^2 = 0 \text{ solve, r} \rightarrow \begin{pmatrix} 0 \\ 1 \end{pmatrix} \nonumber \]
Calculate the probability that an electron in the 1s orbital will be found within one Bohr radius of the nucleus.
\[ \int_0^1 \int_0^{ \pi} \int_0^{2 \pi} \Psi_{1s} (r)^2 r^2 \sin ( \theta ) d \phi d \theta dr \text{ float, 3} \rightarrow .325 \nonumber \]
Find the distance from the nucleus for which the probability of finding a 1s electron is 0.75.
\[ \begin{matrix} a = 2 & \text{Given} & \int_0^a \Psi_{1s} (r)^2 4 \pi r^2 dr = /75 & \text{Find(a) = 1.96} \end{matrix} \nonumber \]
Calculate <T>, <V>, and <r> for the 1s orbital. Is the virial theorem obeyed? Explain.
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{1s} (r) - \frac{1}{2r} \frac{d^2}{dr^2} r \left( \Psi_{1s} (r) \right) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow \frac{1}{2} \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{1s} (r) - \frac{1}{r} \Psi_{1s} (r) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow -1 \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{1s} (r) r \Psi_{1s} (r) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow \frac{3}{2} \nonumber \]
Calculate <T>, <V>, and <r> for the 2s orbital. Is the virial theorem obeyed? Explain.
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2s} (r) - \frac{1}{2r} \frac{d^2}{dr^2} r \Psi_{2s} (r) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow \frac{1}{8} \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2s} (r) - \frac{1}{r} \Psi_{2s} (r) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow - \frac{1}{4} \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2s} (r) r \Psi_{2s} (r) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 6 \nonumber \]
Calculate <T>, <V>, and <r> for the 2py orbital. Is the virial theorem obeyed? Explain.
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2py} (r, ~ \theta,~ \phi ) \begin{bmatrix} - \frac{1}{2r} \frac{d^2}{dr^2} r \Psi_{2py} (r,~ \theta,~ \phi ) ... \\ + \frac{-1}{2r^2 \sin ( \theta)} \left[ \frac{d}{d \theta} \left( \sin ( \theta ) \frac{d}{d \theta} \Psi_{2py} (r,~ \theta,~ \phi ) \right) \right] ... \\ + \frac{-1}{2r^2 \sin ( \theta )^2} \frac{d^2}{d \phi^2} \Phi_{2py} (r,~ \theta,~ \phi) \end{bmatrix} r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow \frac{1}{8} \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2py} (r,~ \theta,~ \phi) - \frac{1}{r} \Psi_{2py} (r,~ \theta,~ \phi) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow \frac{-1}{4} \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2py} (r,~ \theta,~ \phi) r \Psi_{2py} (r,~ \theta,~ \phi) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 5 \nonumber \]
Calculate <T>, <V>, and <r> for the 2pz orbital. Is the virial theorem obeyed? Explain.
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2pz} (r, ~ \theta ) \begin{bmatrix} - \frac{1}{2r} \frac{d^2}{dr^2} r \Psi_{2pz} (r,~ \theta ) ... \\ + \frac{-1}{2r^2 \sin ( \theta)} \left[ \frac{d}{d \theta} \left( \sin ( \theta ) \frac{d}{d \theta} \Psi_{2pz} (r,~ \theta ) \right) \right] ... \\ + \frac{-1}{2r^2 \sin ( \theta )^2} \frac{d^2}{d \phi^2} \Phi_{2pz} (r,~ \theta ) \end{bmatrix} r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow \frac{1}{8} \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2pz} (r,~ \theta ) - \frac{1}{r} \Psi_{2pz} (r,~ \theta ) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow \frac{-1}{4} \nonumber \]
\[ \int_0^{ \infty} \int_0^{ \pi} \int_0^{2 \pi} \Psi_{2pz} (r,~ \theta ) r \Psi_{2pz} (r,~ \theta ) r^2 \sin ( \theta ) d \phi d \theta dr \rightarrow 5 \nonumber \]
Summarize your results in the following table:
\[ \begin{pmatrix} \Psi & \text{T} & \text{V} & \text{E} & \text{r} \\ \text{1s} & 0.5 & -1 & -0.5 & 1.5 \\ \text{2s} & 0.125 & -0.25 & -0.125 & 6 \\ \text{2pz} & 0.125 & -0.25 & -0.125 & 5 \\ \text{2py} & 0.125 & -0.25 & -0.125 & 5 \end{pmatrix} \nonumber \]
Demonstrate that the 1s orbital is an eigenfunction of the energy operator. What is the eigenvalue?
\[ \begin{matrix} T = - \frac{1}{2r} \frac{d^2}{dr^2} r \blacksquare & V = - \frac{1}{r} & H = T + V & \Psi (r) = \frac{1}{ \sqrt{ \pi}} \text{exp} (-r) \end{matrix} \nonumber \]
\[ \frac{- \frac{1}{2r} \frac{d^2}{dr^2} r \Psi_{1s} (r) - \frac{1}{r} \Psi_{2s} (r)}{ \Psi_{1s} (r)} \text{ simplify } \rightarrow \frac{-1}{2} \nonumber \]
Demonstrate that the 2s orbital is an eigenfunction of the energy operator. What is the eigenvalue?
\[ \frac{- \frac{1}{2r} \frac{d^2}{dr^2} r \Psi_{2s} (r) - \frac{1}{r} \Psi_{2s} (r)}{ \Psi_{2s} (r)} \text{ simplify } \rightarrow \frac{-1}{8} \nonumber \]
Demonstrate that the 2py orbital is an eigenfunction of the energy operator. What is the eigenvalue?
\[ \frac{ \begin{bmatrix} - \frac{1}{2r} \frac{d^2}{dr^2} r \Psi_{2py} (r,~ \theta,~ \phi ) ... \\ + \frac{-1}{2r^2 \sin ( \theta)} \left[ \frac{d}{d \theta} \left( \sin ( \theta ) \frac{d}{d \theta} \Psi_{2py} (r,~ \theta,~ \phi ) \right) \right] ... \\ + \frac{-1}{2r^2 \sin ( \theta )^2} \frac{d^2}{d \phi^2} \Phi_{2py} (r,~ \theta, ~ \phi ) \end{bmatrix} - \frac{1}{r} \Psi_{2py} (r,~ \theta,~ \phi)}{ \Psi_{2py} (r,~ \theta,~ \phi)} \text{ simplify } \rightarrow \frac{-1}{8} \nonumber \]