1.52: Analysis of a Temporal Double-slit Experiment
- Page ID
- 155909
Contemporary chemistry is built on a quantum mechanical foundation, and prominent among the fundamental concepts of quantum theory is the superposition principle. Previously the author and others have illustrated the importance of the superposition principle in understanding chemical and physical phenomena [1-5]. Furthermore, the primary literature is replete with manifestations of the quantum superposition in current research [6-8]. Very recently, for example, Hawking and Hertog [9] have published a theory of the origin of the universe based squarely on the superposition princple.
As Richard Feynman demonstrated, the spatial double-slit experiment is a simple and compelling example of the quantum superposition in action [10-11]. All fundamental quantum mechanical phenomena, according to Feynman, can be illuminated by comparison to the double-slit experiment [11].
Now this paradigmatic experiment has a companion in the temporal domain. A temporal doubleslit experiment with attosecond windows was recently reported by an international team led by Gehard Paulus [12]. This note demonstrates that the quantum mechanics behind this remarkable experiment is analogous to that for the spatial double-slit experiment for photons or massive particles.
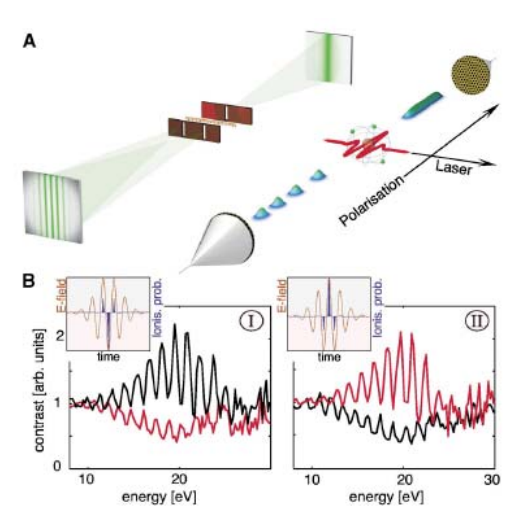
The spatial and temporal experiments for electrons, juxtaposed in Figure 1A [13], are analyzed in terms of conjugate observables united by a Fourier transform. For the spatial experiment the observables are position and momentum, while for the temporal version they are time and energy.
In the spatial double-slit experiment illumination of the slit screen with an electron beam places each electron in a superposition of being simultaneously at slits located at x1 and x2.
\[
|\Psi\rangle=\frac{1}{\sqrt{2}}\left[\left|x_{1}\right\rangle+\left|x_{2}\right\rangle\right] \tag{1}
\nonumber \]
According to quantum mechanical principles spatial localization at two positions leads to delocalization and interference fringes in the electron’s momentum distribution. This can be seen by a Fourier transform of equation (1) into momentum space, initially assuming infinitesimally thin slits.
\[
\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}\left[\left\langle p | x_{1}\right\rangle+\left\langle p | x_{2}\right\rangle\right]=\frac{1}{2 \sqrt{\pi \hbar}}\left[\exp \left(-\frac{i p x_{1}}{\hbar}\right)+\exp \left(-\frac{i p x_{2}}{\hbar}\right)\right] \tag{2}
\nonumber \]
Clearly the two exponential terms will oscillate in and out of phase for various values of the momentum. (See the Appendix for mathematical background on the Dirac brackets used in this paper.) For finite spatial slits of width δ the momentum wave function is given by equation (3)
\[
\langle p | \Psi\rangle=\frac{1}{2 \sqrt{\pi \hbar \delta}} \left[ \int_{x_{1} - \frac{\delta}{2}}^{x_{1} + \frac{\delta}{2}} \exp \left(- \frac{ipx}{\hbar}\right) dx + \int_{x_{2} - \frac{\delta}{2}}^{x_{2} + \frac{\delta}{2}} \exp \left(- \frac{ipx}{\hbar}\right) dx \right] \tag{3}
\nonumber \]
The observed diffraction pattern is actually the electron’s momentum distribution projected onto the detection screen, as is revealed by a graphical representation of \(\left|\langle p| \Psi\rangle\right|^{2}\) [14].
In the temporal double-slit experiment a very short laser pulse (~5 fs), which consists of two maxima (temporal double-slit) and one minimum (temporal single-slit) in the electric field, is used to ionize individual argon atoms.
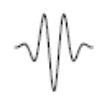
\[
|\Psi\rangle=\frac{1}{\sqrt{2}}\left[\left|t_{1}\right\rangle+\left|t_{2}\right\rangle\right] \tag{4}
\nonumber \]
The kinetic energy of the ionized electron is measured at the detector, and as Figure 1B shows interference fringes are observed in the kinetic energy distribution. A Fourier transform of equation (4) into the energy domain reveals the origin of the fringes; the probability amplitudes for being ionized with kinetic energy E at the two different times interfere constructively and destructively.
\[
\langle E | \Psi\rangle=\frac{1}{\sqrt{2}}\left[\left\langle E | t_{1}\right\rangle+\left\langle E | t_{2}\right\rangle\right]=\frac{1}{2 \sqrt{\pi \hbar}}\left[\exp \left(\frac{i E t_{1}}{\hbar}\right)+\exp \left(\frac{i E t_{2}}{\hbar}\right)\right] \tag{5}
\nonumber \]
For finite windows of time duration \(\delta\) equation (5) becomes,
\[
\langle E | \Psi\rangle=\frac{1}{2 \sqrt{\pi \hbar \delta}} \left[ \int_{t_{1} - \frac{\delta}{2}}^{t_{1} + \frac{\delta}{2}} \exp \left(- \frac{iEt}{\hbar}\right) dt + \int_{x_{2} - \frac{\delta}{2}}^{x_{2} + \frac{\delta}{2}} \exp \left(- \frac{iEt}{\hbar}\right) dt \right] \tag{6}
\nonumber \]
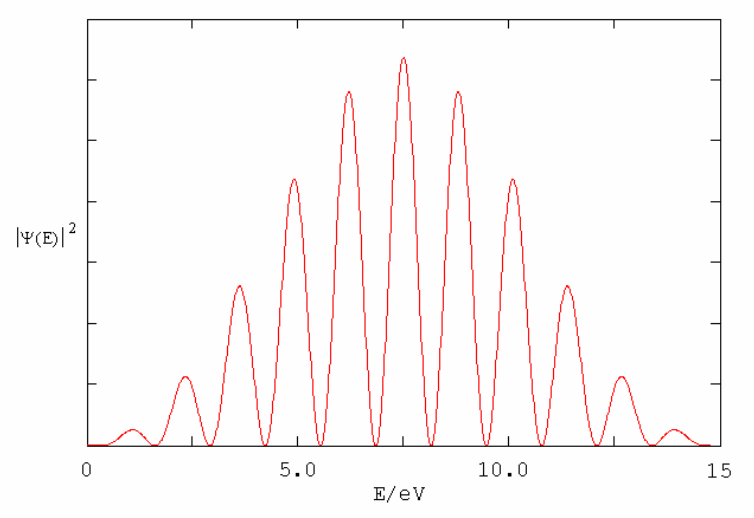
Figure 2 shows that a plot of \(|\langle E | \Psi\rangle|^{2}\) vs E using equation (6) with estimates for t1, t2 (\(\Delta\)t) and \(\detla\) from reference [12] generates a 15 eV envelope with 11 prominent interference fringes. This calculated result is in reasonable quantitative agreement with the experimental data displayed in Figure 1B.
The temporal double-slit diffraction pattern reported in reference [12] is a single-electron effect – only one ionized electron is being observed at a time. Likewise the spatial analog has been performed at low source intensity such that there is only one electron in the apparatus at a time [15,16]. The fact that an interference pattern is observed under single-particle conditions leads to terms such as single-particle interference or self-interference. Glauber [17] has argued against such language because it is physically misleading.
The things that interfere in quantum mechanics are not particles. They are probability amplitudes for certain events. It is the fact that probability amplitudes add up like complex numbers that is responsible for all quantum mechanical interferences.
The interference of probability amplitudes that Glauber identifies as the source of all quantum mechanical interference phenomena is clearly revealed in the mathematical analysis provided in this note; it is especially clear in equations (2) and (5).
Appendix
A one-dimensional plane wave traveling in the positive x-direction has the following mathematical form.
\[
F(x, t)=\exp \left(i \frac{2 \pi x}{\lambda}\right) \exp (-i 2 \pi v t)
\nonumber \]
Substitution of h/p for \(\lambda\) (de Broglie) and E/h for \(\nu\) (Planck/Einstein) transforms F(x,t) into a quantum mechanical free-particle wave function.
\[
\Psi(x, t)=\exp \left(\frac{i p x}{\hbar}\right) \exp \left(-\frac{i E t}{\hbar}\right)
\nonumber \]
Assigning Dirac brackets containing the complementary observable pairs to this equation yields,
\[
\langle x | p\rangle=\exp \left(\frac{i p x}{\hbar}\right) \quad \text { and } \quad\langle t | E\rangle=\exp \left(-\frac{i E t}{\hbar}\right)
\nonumber \]
Dirac notation reveals that these equations are Fourier transforms between complementary variables. The complex conjugates of these relations are used in the analysis presented in this paper.
\[
\langle p | x\rangle=\langle x | p\rangle^{*}=\exp \left(-\frac{i p x}{\hbar}\right) \text { and } \quad\langle E | t\rangle=\langle t | E\rangle^{*}=\exp \left(\frac{i E t}{\hbar}\right)
\nonumber \]
Additional information on Dirac notation is available online [18].
Acknowledgment
I wish to acknowledge helpful comments by Professor Gerhard Paulus of Max-Planck-Institut für Quantenoptik, Ludvig-Maximilians-Universität München, and Texas A&M University.
References
- McMillin, D. R. “Fluctuating Electric Dipoles and the Absorption of Light,” J. Chem. Educ. 1978, 55, 7-11.
- Weinhold, F. A. “Chemical Bonding as a Superposition Phenomenon,” J. Chem. Educ. 1999, 76, 1141-1146.
- Baskin, J. S.; Zewail, A. H. “Freezing Atoms in Motion: Principles of Femtochemistry and Demonstration by Laser Stroboscopy,” J. Chem. Educ. 2001, 78, 737-751.
- Rioux, F.; Johnson, B. J. “Using Optical Transforms to Teach Quantum Mechanics,” Chem. Educator 2004, 9, 12-16.
- Rioux, F. “Illustrating the Superposition Principle with Single-Photon Interference,” Chem. Educator 2005, 10, 424-426.
- Dixon, R. N.; Hwang, D. W.; Yang, X. F.; Harich, S.; Lin, J. J.; Yang. X. “Chemical ‘Double Slits’: Dynamical Interference of Photodissociation Pathways in Water,” Science, 1999, 285, 1249-1253.
- van der Wal, C. H.; ter Haar, A. C. J.; Wilhelm, F. K.; Schouten, R. N.; Harmans, C. J. P. M.; Orlando, T. P.; Lloyd, S.; Mooij, J. E. “Quantum Superposition of Macroscopic Persistent-Current States,” Science, 2000, 290, 773-777.
- Weinhold, F. “A new twist on molecular shape,” Nature 2001, 411, 539-541 (and references quoted therein).
- Hawking, S. W.; Hertog, T. “Populating the landscape: A top-down approach,” Phys. Rev. D 2006, 73 123527.
- Feynman, R. P.; Leighton, R. B.; Sands, M. The Feynman Lectures on Physics, Vol. 3; Addison-Wesley: Reading, 1965, p. 1-1.
- Feynman, R. P. The Character of Physical Law; MIT Press: Cambridge, 1967; p. 130.
- Lindner, F.; Schätzel, M. G.; Walther, H.; Baltuška, A.; Goulielmakis, E.; Krausz, F.; Milošević, D. B.; Bauer, D.; Becker, W.; Gaulus, G. G. “Attosecond Double-Slit Experiment,” Phys. Rev. Lett. 2005, 95, 040401.
- Physics World and PhysicsWeb (www.physicsweb.org/articles/news/9/3/1/1)
- Marcella, T. V. “Quantum interference with slits,” Eur. J. Phys. 2002, 23, 615-621.
- Merli P. G.; Missiroli G. F.; Pozzi G. “On the statistical aspects of electron interference phenomena,” Am. J. Phys. 1976, 44, 306-307.
- Tonomura A.; Endo, T.; Matsuda, T.; Kawasaki, T.; Ezawa, H. “Demonstration of singleelectron buildup of an interference pattern,” Am. J. Phys. 1989, 57, 117-120.
- Glauber, R. “Dirac’s Famous Dictum on Interference: One Photon or Two?” Am. J. Phys. 1995, 63, 12.
- Tutorial on Dirac notation