1.53: An Analysis of Three‐Path Interference

Quantum mechanics teaches that if there is more than one path to a particular destination interference effects are likely. Using Feynmanʹs sum over historiesʹ approach to quantum mechanics the probability of arrival at a location is the square of the magnitude of the sum of the probability amplitudes for each path to that location. For example, in a triple‐slit diffraction experiment the probability of arriving at x on the detection screen in Dirac notation is,

\[
P_{123}=|\langle x | S\rangle|^{2}=|\langle x | 3\rangle\langle 3 | S\rangle+\langle x | 2\rangle\langle 2 | s\rangle+\langle x | 1\rangle\langle\left.(1 | s)\right|^{2}
\nonumber \]

The single‐photon interferometer shown below [Franson, Science 329, 396 (2010)] is a close cousin of the triple‐slit experiment because it provides three paths to the detector. Initially we will ignore the other two output channels A and B.

Three Path Interference

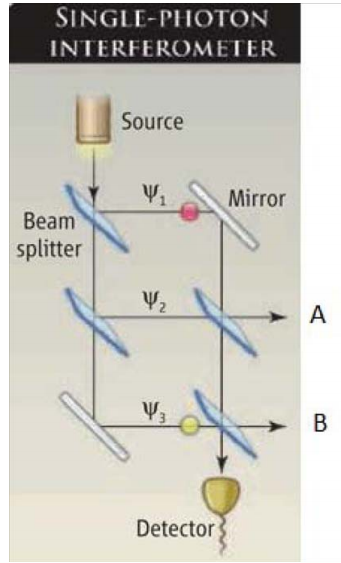
Probability Amplitudes

In this analysis the probability amplitudes are calculated using the following conventions.

Assume 50‐50 beam splitters and assign \(\frac{\pi}{2}\) (i) phase shift to reflection (usual convention).

Transmission at a beam splitter: \(\mathrm{T} :=\frac{1}{\sqrt{2}}\)

Reflection at a beam splitter: \(\mathrm{R} :=\frac{\mathrm{i}}{\sqrt{2}}\)

Reflection at a mirror: \(M : = 1\)

First, using Feynmanʹs ʹsum over historiesʹ method we calculate the probability that the photon will arrive at the Detector (3 paths):

\[
(|\mathrm{R} \cdot \mathrm{M} \cdot \mathrm{T} \cdot \mathrm{T}+\mathrm{T} \cdot \mathrm{R} \cdot \mathrm{R} \cdot \mathrm{T}+\mathrm{T} \cdot \mathrm{T} \cdot \mathrm{M} \cdot \mathrm{R}|)^{2}=0.5625
\nonumber \]

To establish that probability is conserved the probabilities for arrival at A and B are calculated.

Calculate the probability that the photon will arrive at A (2 paths):

\[
(|\mathrm{T} \cdot \mathrm{R} \cdot \mathrm{T}+\mathrm{R} \cdot \mathrm{M} \cdot \mathrm{R}|)^{2}=0.375
\nonumber \]

Calculate the probability that the photon will arrive at B (3 paths):

\[
(|\mathrm{R} \cdot \mathrm{M} \cdot \mathrm{T} \cdot \mathrm{R}+\mathrm{T} \cdot \mathrm{R} \cdot \mathrm{R} \cdot \mathrm{R}+\mathrm{T} \cdot \mathrm{T} \cdot \mathrm{M} \cdot \mathrm{T}|)^{2}=0.0625
\nonumber \]

Demonstrate that probability is conserved:

\[
0.5625+0.375+0.0625=1
\nonumber \]

While this traditional analysis postulates three‐path interference for the arrival probability at the detector, Sinha et al. [Science 329, 418 (2010)] argue that true interference only occurs between pairs of paths. In this case between paths 1 & 2, 1 & 3, and 2 & 3. Franson summarized this view as follows: ʺQuantum interference between many different pathways is simply the sum of the effects from all pairs of pathways.ʺ

The probability expression for an event involving two equivalent paths is

\[
P_{i j}=\left|\Psi_{i}+\Psi_{j}\right|^{2}=\left|\Psi_{i}\right|^{2}+\left|\Psi_{j}\right|^{2}+\Psi_{i}^{*} \Psi_{j}+\Psi_{j}^{*} \Psi_{i}=P_{i}+P_{j}+I_{i j}
\nonumber \]

where I_ij is the interference term and P_i is defined as the probability when only the i^th path is open. It is my opinion that this latter designation is not strictly valid. However, accepting it for the time being leads to the following definition for two‐path interference.

\[
I_{i j}=P_{i j}-P_{i}-P_{j}
\nonumber \]

Therefore, the probability for an event involving three equivalent paths to a destination using only two‐path interference is,

\[
P_{123}=P_{1}+P_{2}+P_{3}+I_{12}+I_{13}+I_{23}=P_{12}+P_{13}+P_{23}-P_{1}-P_{2}-P_{3}
\nonumber \]

The probabilities in this equation are now calculated.

\( \mathrm{P}_{1} \quad(|\mathrm{R} \cdot \mathrm{M} \cdot \mathrm{T} \cdot \mathrm{T}|)^{2}=0.125 \)	\( \mathrm{P}_{2} \quad(|\mathrm{T} \cdot \mathrm{R} \cdot \mathrm{R} \cdot \mathrm{T}|)^{2}=0.0625 \)	\( \mathrm{P}_{3} \quad(|\mathrm{T} \cdot \mathrm{T} \cdot \mathrm{M} \cdot \mathrm{R}|)^{2}=0.125 \)
\( \mathrm{P}_{12} \quad(|\mathrm{R} \cdot \mathrm{M} \cdot \mathrm{T} \cdot \mathrm{T}+\mathrm{T} \cdot \mathrm{R} \cdot \mathrm{R} \cdot \mathrm{T}|)^{2}=0.1875 \)	\( \mathrm{P}_{13} \quad(|\mathrm{R} \cdot \mathrm{M} \cdot \mathrm{T} \cdot \mathrm{T}+\mathrm{T} \cdot \mathrm{T} \cdot \mathrm{M} \cdot \mathrm{R}|)^{2}=0.5 \)
\( \mathrm{P}_{23} \quad(|\mathrm{T} \cdot \mathrm{R} \cdot \mathrm{R} \cdot \mathrm{T}+\mathrm{T} \cdot \mathrm{T} \cdot \mathrm{M} \cdot \mathrm{R}|)^{2}=0.1875 \)

The probability of arriving at a detector which can be reached by three paths, but using only two‐path interference is,

\[
\mathrm{P}_{12}+\mathrm{P}_{13}+\mathrm{P}_{23}-\mathrm{P}_{1}-\mathrm{P}_{2}-\mathrm{P}_{3}=0.5625
\nonumber \]

Clearly this result does not prove that ʺQuantum interference between many different pathways is simply the sum of the effects from all pairs of pathways.ʺ Why is it necessary to subtract P₁, P₂ and P₃ from the two‐path interference terms if they are what itʹs all about?

The previous Feynman calculation produces the same result using a more transparent method; add the probability amplitudes for the three paths to the detector and square the absolute magnitude.

\[
\left(\left|A_{1}+A_{2}+A_{3}\right|\right)^{2}=0.5625
\nonumber \]

\[
(|\mathrm{R} \cdot \mathrm{M} \cdot \mathrm{T} \cdot \mathrm{T}+\mathrm{T} \cdot \mathrm{R} \cdot \mathrm{R} \cdot \mathrm{T}+\mathrm{T} \cdot \mathrm{T} \cdot \mathrm{M} \cdot \mathrm{R}|)^{2}=0.5625
\nonumber \]

Objection to the Definitions

Sinha et al. write the double‐slit wave function (unnormalized) as a linear superposition of the photon taking two paths (A and B) to the detector. The square modulus of the wave function gives the probability expression.

\[
|\Psi|^{2}=\left|\psi_{A}\right|^{2}+\left|\psi_{B}\right|^{2}+\psi_{A}^{*} \psi_{B}+\psi_{B}^{*} \psi_{A}
\nonumber \]

Obviously this is just traditional quantum mechanical mathematical procedure. The problem I have is with the interpretation or partition of this equation that comes next. The authors write the probability expression as

\[
|\Psi|^{2}=P_{A}+P_{B}+I_{A B}
\nonumber \]

where P_A(P_B) is the probability that only slit A(B) is open and the remaining terms represent the actual interference. I do not believe this sort of partitioning of the terms of \(|\Psi|^{2}\) is quantum mechanically legitimate. If only slit A is open then the wave function is \(\Psi=\Psi_{\mathrm{A}}\) and not \(\Psi=\Psi_{\mathrm{A}}+\Psi_{\mathrm{B}}\). It is incorrect to say, in the double‐slit experiment, that \(\left|\Psi_{\mathrm{A}}\right|^{2}\) is the probability that the photon goes through slit A.

As Roy Glauber has written [AJP 63, 12 (1995)], ʺThe things that interfere in quantum mechanics ... are the probability amplitudes for certain events.ʺ The triple‐slit experiment involves the interference of three probability amplitudes because there are three paths from the source (S) to each position (x) on the detection screen. According to quantum fundamentals, each photon takes all three paths simultaneously.

\[
\Psi_{133}=\langle x | S\rangle=\langle x | 3\rangle\langle 3 | S\rangle+\langle x | 2\rangle\langle 2 | S\rangle+\langle x | 1\rangle\langle1|S\rangle
\nonumber \]

In Chapter 3 of Volume III of The Feynman Lectures on Physics, Feynman discusses a diffraction experiment in which a two‐slit screen followed by a three‐slit screen are placed before the detection screen providing six paths to any point on the detection screen. Feynmanʹs analysis leads to the following probability amplitude for the particle to be detected at x.

\[
\langle x | S\rangle=\langle x | a\rangle\langle a | 1\rangle\langle 1 | S\rangle+\langle x | b\rangle\langle b | 1\rangle\langle 1 | S\rangle+\langle x | c\rangle\langle c | 1\rangle\langle 1 | S\rangle +\langle x | a\rangle\langle a | 2\rangle\langle 2 | S\rangle+\langle x | b\rangle\langle b | 2\rangle\langle 2 | S\rangle+\langle x | c\rangle\langle c | 2\rangle\langle 2 | S\rangle
\nonumber \]

Or more succinctly (Feynmanʹs equation 3.6 on page 3‐4 of Volume III)

\[
\langle x | S\rangle=\sum_{i=1,2 \atop \alpha=a, b, c}\langle x | \alpha\rangle\langle\alpha | i\rangle\langle i | S\rangle
\nonumber \]

In summary, these superpositions of probability amplitudes are simple examples of Feynmanʹs sum‐over‐histories approach to quantum mechanics, of which the double‐slit experiment is the simplest example. It is clear that pair wise interference is not suggested in this approach, except for the double‐slit experiment and then only because in that case there are only two paths. Feynmanʹs rule is, sum the amplitudes for all paths to allow for interference before squaring the absolute magnitude of the sum to obtain the probability.

Freeman Dyson had the following reaction when he first heard of Feynmanʹs novel approach to quantum mechanics. ʺThirty‐one years ago, Dick Feynman told me about his ʹsum over historiesʹ version of quantum mechanics. ʹThe electron does anything it likes,ʹ he said. ʹIt just goes in any direction, at any speed, forward or backward in time, however it likes, and then you add up the amplitudes and it gives you the wave function.ʹ I said to him ʹYouʹre crazy.ʹ But he isnʹt.ʺ