1.29: Single Slit Diffraction and the Fourier Transform
- Page ID
- 143936
| Slit width: \(w : = 1\) | Coordinate‐space wave function: \(\Psi(x, w) :=\text { if }\left[\left(x \geq-\frac{w}{2}\right) \cdot\left(x \leq \frac{w}{2}\right), 1,0\right]\) |
\[
x :=\frac{-w}{2}, \frac{-w}{2}+.005 \dots \frac{w}{2}
\nonumber \]

A Fourier transform of the coordinate‐space wave function yields the momentum wave function and the momentum distribution function, which is the diffraction pattern.
\[
\Phi\left(\mathrm{p}_{\mathrm{X}}, \mathrm{w}\right) :=\frac{1}{\sqrt{2 \cdot \pi \cdot \mathrm{w}}} \cdot \int_{-\frac{\mathrm{w}}{2}}^{\frac{\mathrm{w}}{2}} \exp \left(-\mathrm{i} \cdot \mathrm{p}_{\mathrm{x}} \cdot \mathrm{x}\right) \mathrm{dx} \text { simplify } \rightarrow \frac{\sqrt{2} \cdot \sin \left(\frac{\mathrm{p}_{\mathrm{x}} \cdot \mathrm{w}}{2}\right)}{\sqrt{\pi} \cdot \mathrm{p}_{\mathrm{x}} \cdot \sqrt{\mathrm{w}}}
\nonumber \]
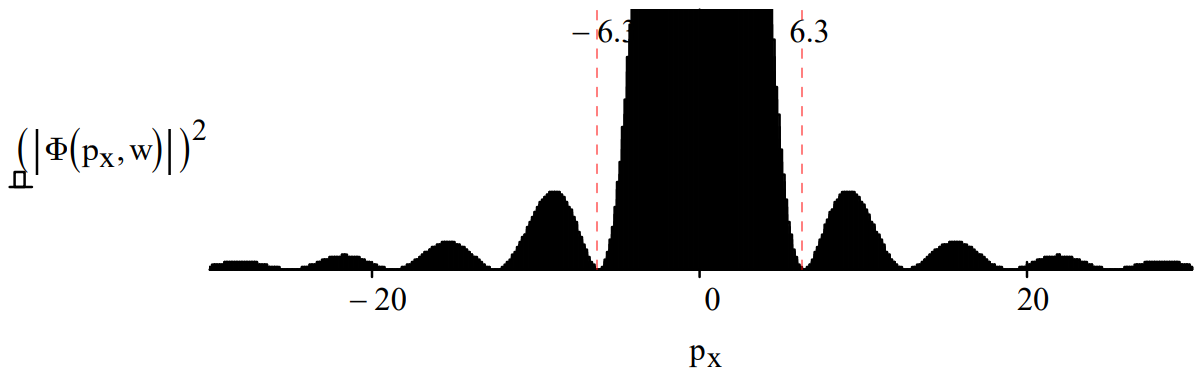
Now Fourier transform the momentum wave function back to coordinate space and display result. This is done numerically using large limits of integration for momentum.
\[
\Psi(x, w) :=\int_{-5000}^{5000} \frac{\frac{1}{2} \sin \left(\frac{1}{2} \cdot w \cdot p_{x}\right)}{\pi^{\frac{1}{2}} \cdot w^{\frac{1}{2}} \cdot p_{x}} \cdot \frac{\exp \left(i \cdot p_{x^{*}} x\right)}{\sqrt{2 \cdot \pi}} d p_{x}
\nonumber \]


