1.16: Quantum Mechanics and the Fourier Transform
- Page ID
- 143627
Moving on to the hydrogen atom, we can use the spatial and momentum wave functions for the 1s, 2s and 3s energy states to again illustrate visually the uncertainty principle.
The Position‐Momentum Uncertainty Relation in the Hydrogen Atom
The hydrogen atom coordinate and momentum wave functions can be used to illustrate the uncertainty relation involving position and momentum.
The 1s wave function is used to calculate the average distance of the electron from the nucleus.
\[
\Psi_{1 s}(r) :=\frac{1}{\sqrt{\pi}} \cdot \exp (-r) \quad \mathrm{r}_{\mathrm{ls}} :=\int_{0}^{\infty} \mathrm{r} \cdot \Psi_{1 \mathrm{s}}(\mathrm{r})^{2} \cdot 4 \cdot \pi \cdot \mathrm{r}^{2} \mathrm{d} \mathrm{r} \quad r_{1 s}=1.500
\nonumber \]
The Fourier transform of the 1s wave function yields the momentum wave function. The momentum wave function is used to calculate the average magnitude of the electron momentum.
\[
\Phi_{1 s}(\mathrm{p}) :=\frac{1}{\sqrt{8 \cdot \pi^{3}}} \cdot \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2 \cdot \pi} \Psi_{1 s}(\mathrm{r}) \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{r} \cdot \cos (\theta)) \cdot \mathrm{r}^{2} \cdot \sin (\theta) \mathrm{d} \phi \mathrm{d} \theta \mathrm{dr} \\ \rightarrow 2 \cdot \frac{2^{\frac{1}{2}}}{\pi \cdot[(-1)+\mathrm{i} \cdot \mathrm{p}]^{2} \cdot(1+\mathrm{i} \cdot \mathrm{p})^{2}}
\nonumber \]
\[
\mathrm{p}_{\mathrm{ls}} :=\int_{0}^{\infty} \mathrm{p} \cdot\left(\left|\Phi_{1 \mathrm{s}}(\mathrm{p})\right|\right)^{2} \cdot 4 \cdot \pi \cdot \mathrm{p}^{2} \mathrm{d} \mathrm{p} \quad \quad \mathrm{p}_{1 \mathrm{s}}=0.849
\nonumber \]
The 2s wave function is used to calculate the average distance of the electron from the nucleus.
\[
\Psi_{2 s}(r) :=\frac{1}{\sqrt{32 \cdot \pi}} \cdot(2-r) \cdot \exp \left(-\frac{r}{2}\right) \quad \mathrm{r}_{2 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{r} \cdot \Psi_{2 \mathrm{s}}(\mathrm{r})^{2} \cdot 4 \cdot \pi \cdot \mathrm{r}^{2} \mathrm{dr} \quad \mathrm{r}_{2 \mathrm{s}}=6.000
\nonumber \]
The Fourier transform of the 2s wave function yields the momentum wave function. The momentum wave function is used to calculate the average magnitude of the electron momentum.
\[
\Phi_{2 s}(\mathrm{p}) :=\frac{1}{\sqrt{8 \cdot \pi^{3}}} \cdot \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2 \cdot \pi} \Psi_{2 \mathrm{s}}(\mathrm{r}) \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{r} \cdot \cos (\theta)) \cdot \mathrm{r}^{2} \cdot \sin (\theta) \mathrm{d} \phi \mathrm{d} \theta \mathrm{dr} \; \text{simplify} \\ \rightarrow \frac{-16}{\pi} \cdot \frac{(-1)+4 \cdot p^{2}}{[(-1)+2 \cdot i \cdot p]^{3} \cdot(1+2 \cdot i \cdot p)^{3}}
\nonumber \]
\[
\mathrm{p}_{2 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{p} \cdot\left(\left|\Phi_{2 \mathrm{s}}(\mathrm{p})\right|\right)^{2} \cdot 4 \cdot \pi \cdot \mathrm{p}^{2} \mathrm{d} \mathrm{p} \quad \quad \mathrm{p}_{2 \mathrm{s}}=0.340
\nonumber \]
The 3s wave function is used to calculate the average distance of the electron from the nucleus.
\[
\Psi_{3 \mathrm{s}}(\mathrm{r}) :=\frac{1}{81 \cdot \sqrt{3 \cdot \pi}} \cdot\left(27-18 \cdot \mathrm{r}+2 \cdot \mathrm{r}^{2}\right) \exp \left(\frac{-\mathrm{r}}{3}\right) \quad \mathrm{r}_{3 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{r} \cdot \Psi_{3 \mathrm{s}}(\mathrm{r})^{2} \cdot 4 \cdot \pi \cdot \mathrm{r}^{2} \mathrm{dr} \quad \mathrm{r}_{3 \mathrm{s}}=13.500
\nonumber \]
The Fourier transform of the 3s wave function yields the momentum wave function. The momentum wave function is used to calculate the average magnitude of the electron momentum.
\[
\Phi_{3 \mathrm{s}}(\mathrm{p}) :=\frac{1}{\sqrt{8 \cdot \pi^{3}}} \cdot \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2 \cdot \pi} \Psi_{3 s}(\mathrm{r}) \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{r} \cdot \cos (\theta)) \cdot \mathrm{r}^{2} \cdot \sin (\theta) \mathrm{d} \phi \mathrm{d} \theta \mathrm{dr} \; \text{simplify} \\ \rightarrow 18 \cdot \frac{2^{\frac{1}{2}}}{\pi} \cdot 3^{\frac{1}{2}} \cdot \frac{1-30 \cdot \mathrm{p}^{2}+81 \cdot \mathrm{p}^{4}}{[(-1)+3 \cdot \mathrm{i} \cdot \mathrm{p}]^{4} \cdot(1+3 \cdot \mathrm{i} \cdot \mathrm{p})^{4}}
\nonumber \]
\[
\mathrm{p}_{3 s} :=\int_{0}^{\infty} \mathrm{p} \cdot\left(\left|\Phi_{3 s}(\mathrm{p})\right|\right)^{2} \cdot 4 \cdot \pi \cdot \mathrm{p}^{2} \mathrm{d} \mathrm{p} \quad \quad \mathrm{p}_{3 \mathrm{s}}=0.218
\nonumber \]
These results can be summarize in both tabular and graphical form.
\[
\left( \begin{array}{cccc}{\text { Orbital}} & \text{ AveragePosition } & {\text { AverageMomentum }} \\ {1 \mathrm{s}} & {1.5} & {0.849} \\ {2 \mathrm{s}} & {6.0} & {0.340} \\ {3 \mathrm{s}} & {13.5} & {0.218}\end{array}\right)
\nonumber \]
The table shows that the average distance of the electron from the nucleus increases from 1s to 3s, indicating an increase in the uncertainty in the location of the electron. At the same time the average magnitude of electron momentum decreases from 1s to 3s, indicating a decrease in momentum uncertainty. The spatial and momentum distribution functions shown below illustrate this effect graphically.
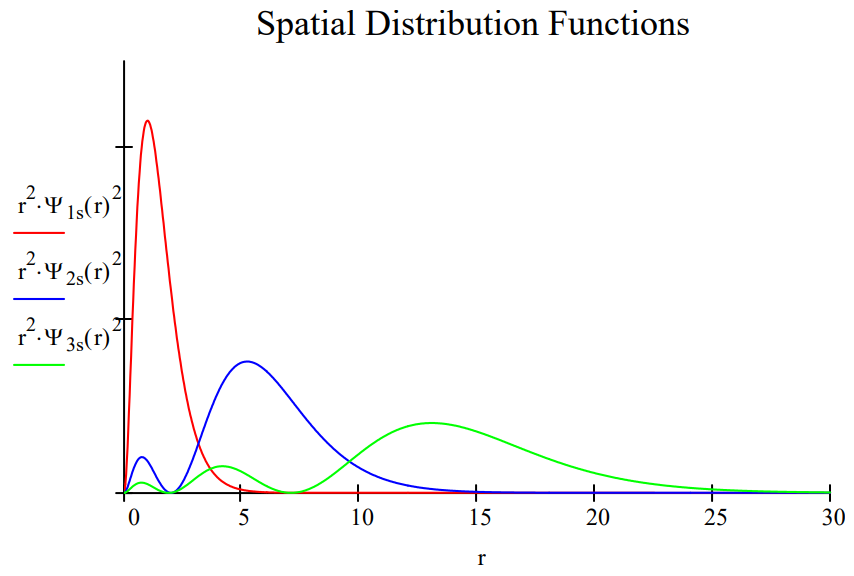
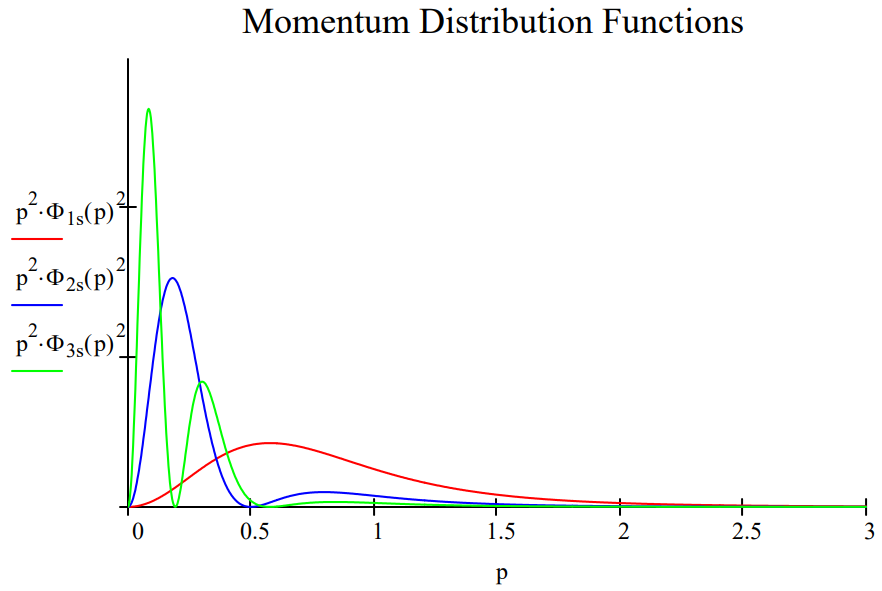
In addition to the coordinate and momentum representation, there is also the phase space approach to quantum mechanics, which physicist in particular find useful. It combines the coordinate and momentum approaches and requires a phase-space distribution function such as the Wigner function. The following tutorial illustrates the computational consistency of the three approaches to quantum mechanics. Two related tutorials dealing with quantum mechanical tunneling and the repackaging of quantum weirdness are also available.
Quantum Tunneling in Coordinate, Momentum and Phase Space
A study of quantum mechanical tunneling brings together the classical and quantum mechanical points of view. In this tutorial the harmonic oscillator will be used to analyze tunneling in coordinate-, momentum- and phase-space. The Appendix provides the position and momentum operators appropriate for these three representations.
The classical equation for the energy of a harmonic oscillator is,
\[
\mathrm{E}=\frac{\mathrm{p}^{2}}{2 \cdot \mu}+\frac{1}{2} \cdot \mathrm{k} \cdot \mathrm{x}^{2}
\nonumber \]
The quantum mechanical counter part is Schrödinger's equation (in atomic units, h = 2 \(\pi\)),
\[
\frac{-1}{2 \cdot \mu} \cdot \frac{\mathrm{d}^{2}}{\mathrm{dx}^{2}} \Psi(\mathrm{x})+\frac{1}{2} \cdot \mathrm{k} \cdot \mathrm{x}^{2} \cdot \Psi(\mathrm{x})=\mathrm{E} \cdot \Psi(\mathrm{x})
\nonumber \]
In atomic units the quantum mechanical wave function in coordinate space for the harmonic oscillator ground state with reduced mass \(\mu\) and force constant k is given by,
\[
\Psi(\mathrm{x}, \mathrm{k}, \mu) :=\left(\frac{\sqrt{\mathrm{k} \cdot \mu}}{\pi}\right)^{\frac{1}{4}} \cdot \exp \left(-\sqrt{\mathrm{k} \cdot \mu} \cdot \frac{\mathrm{x}^{2}}{2}\right)
\nonumber \]
In the interest of mathematical simplicity and expediency we will use k = \(\mu\) =1. The normalized ground state wave function under these conditions is,
\[
\Psi(x) :=\left(\frac{1}{\pi}\right)^{\frac{1}{4}} \cdot \exp \left(\frac{-x^{2}}{2}\right) \qquad \int_{-\infty}^{\infty} \Psi(x)^{2} d x=1
\nonumber \]
Solving Schrödinger's equation for this wave function yields a ground state energy of 0.5 in atomic units.
\[
\frac{-1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{dx}^{2}} \Psi(\mathrm{x})+\frac{1}{2} \cdot \mathrm{x}^{2} \cdot \Psi(\mathrm{x})=\mathrm{E} \cdot \Psi(\mathrm{x}) \text { solve, } \mathrm{E} \rightarrow \frac{1}{2}
\nonumber \]
Classically a harmonic oscillator, like a pendulum, has a turning point when kinetic energy is zero and the pendulum bob changes direction. The turning point is calculated as follows using the classical expression for the energy.
\[
\frac{1}{2}=\frac{1}{2} \cdot \mathrm{x}^{2} \text { solve, } \mathrm{x} \rightarrow \left( \begin{array}{c}{1} \\ {-1}\end{array}\right)
\nonumber \]
Thus, the permissible range of position values is between -1 and +1. Position values outside this range are classically forbidden. However, quantum theory permits position values for which the total energy is less than the potential energy. This is referred to as quantum tunneling. The probability that tunneling is occurring is calculated below.
\[
2 \cdot \int_{1}^{\infty} \Psi(x)^{2} d x=0.157
\nonumber \]
Next we move to a similar calculation in momentum space. First the coordinate wave function is Fourier transformed into momentum space and normalization is demonstrated.
\[
\Phi(\mathrm{p}) :=\frac{1}{\sqrt{2 \cdot \pi}} \cdot \int_{-\infty}^{\infty} \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \Psi(\mathrm{x}) \mathrm{dx} \rightarrow \frac{1}{\pi^{\frac{1}{4}}} \cdot \mathrm{e}^{\frac{-1}{2} \cdot \mathrm{p}^{2}} \qquad \int_{-\infty}^{\infty}(|\Phi(\mathrm{p})|)^{2} \mathrm{d} \mathrm{p}=1
\nonumber \]
Solving Schrödinger's equation in momentum space naturally gives the same energy eigenvalue.
\[
\frac{\mathrm{p}^{2}}{2} \cdot \Phi(\mathrm{p})-\frac{1}{2} \cdot \frac{\mathrm{d}^{2}}{\mathrm{dp}^{2}} \Phi(\mathrm{p})=\mathrm{E} \cdot \Phi(\mathrm{p}) \text { solve, } \mathrm{E} \rightarrow \frac{1}{2}
\nonumber \]
And we find that the classically permissible range of momentum values is the same given the reduced mass and force constant values used in these calculations.
\[
\frac{1}{2}=\frac{\mathrm{p}^{2}}{2} \text { solve, } \mathrm{p} \rightarrow \left( \begin{array}{c}{1} \\ {-1}\end{array}\right)
\nonumber \]
Next we see that the tunneling probability in momentum space is the same as it is in coordinate space.
\[
2 \cdot \int_{1}^{\infty} \Phi(\mathrm{p})^{2} \mathrm{dp}=0.157
\nonumber \]
Moving to phase space requires a distribution function that depends on both position and momentum. The Wigner function fits these requirements and is generated here using both the coordinate and momentum wave functions. Please see “Examining the Wigner Distribution Using Dirac Notation,” arXiv: 0912.2333 (2009) for further detail.
\[
\mathrm{W}(\mathrm{x}, \mathrm{p}) :=\frac{1}{2 \cdot \pi} \cdot \int_{-\infty}^{\infty} \Psi\left(\mathrm{x}+\frac{\mathrm{s}}{2}\right) \cdot \exp (\mathrm{i} \cdot \mathrm{s} \cdot \mathrm{p}) \cdot \Psi\left(\mathrm{x}-\frac{\mathrm{s}}{2}\right) \mathrm{ds} \rightarrow \frac{1}{\pi} \cdot \mathrm{e}^{\left(-\mathrm{x}^{2}\right)-\mathrm{p}^{2}}
\nonumber \]
\[
\mathrm{W}(\mathrm{x}, \mathrm{p}) :=\frac{1}{2 \cdot \pi} \cdot \int_{-\infty}^{\infty} \Phi\left(\mathrm{p}+\frac{\mathrm{s}}{2}\right) \cdot \exp (\mathrm{i} \cdot \mathrm{s} \cdot \mathrm{x}) \cdot \Phi\left(\mathrm{p}-\frac{\mathrm{s}}{2}\right) \mathrm{ds} \rightarrow \frac{1}{\pi} \cdot \mathrm{e}^{\left(-\mathrm{x}^{2}\right)-\mathrm{p}^{2}}
\nonumber \]
The Wigner function is normalized over position and momentum, and yields the appropriate energy expectation value for the ground state of the harmonic oscillator.
\[
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \mathrm{W}(\mathrm{x}, \mathrm{p}) \mathrm{dx} \mathrm{d} \mathrm{p}=1 \qquad \int_{-\infty}^{\infty} \int_{-\infty}^{\infty}\left(\frac{p^{2}}{2}+\frac{x^{2}}{2}\right) \cdot \mathrm{W}(\mathrm{x}, \mathrm{p}) \mathrm{d} \mathrm{x} \mathrm{d} \mathrm{p}=0.5
\nonumber \]
Tunneling probability in phase space is calculated as follows:
\[
4 \int_{1}^{\infty} \int_{1}^{\infty} \mathrm{W}(\mathrm{x}, \mathrm{p}) \mathrm{d} \mathrm{x} \mathrm{dp}=0.025
\nonumber \]
This is in agreement with the separate coordinate and momentum space calculations which gave values of 0.157.
\[
0.157 \cdot 0.157=0.025
\nonumber \]
Appendix
The table lists the forms of the position and momentum operators in the coordinate, momentum and phase space representations. Clearly the multiplicative character of the phase space operators appeals to our classical prejudices and intuition. However, we must remind ourselves that the phase space distribution function on which they "operate" is generated from either the coordinate or momentum wave function. In the coordinate representation the momentum operator is differential; in the momentum representation the coordinate operator is differential. As is shown in other tutorials in this series, the apparent "classical character" of the phase space representation only temporarily hides the underlying quantum weirdness.
\[\begin{pmatrix} \text{Operator} & \text{CoordinateSpace} & \text{MomentumSpace} & \text{PhaseSpace} \\ \text{position} & x \cdot \Box & i \cdot \frac{d}{dp} \Box & x \cdot \Box \\ \text{momentum} & \frac{1}{i} \cdot \frac{d}{dx} \Box & p \cdot \Box & p \cdot \Box \end{pmatrix} \nonumber \]

