1.13: Quantum Mechanics and the Fourier Transform
- Page ID
- 143474
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Wave-particle duality as expressed by the de Broglie wave equation
\[
\lambda=\frac{h}{m v}=\frac{h}{p}
\nonumber \]
is the seminal concept of quantum mechanics. On the left side we have the wave property, wavelength, and on the right in a reciprocal relationship mediated by the ubiquitous Planck’s constant, we have the particle property, momentum.
Wave and particle are physically incompatible concepts because waves are spatially delocalized, while particles are spatially localized. In spite of this incongruity we find in quantum theory that they are necessary companions in the analysis of atomic and molecular phenomena. Both concepts are required for a complete examination of experiments at the nanoscale level.
This view can be summarized by saying that in quantum-level experiments we always detect particles, but we predict or interpret the experimental outcome by assuming wavelike behavior prior to particle detection. As Bragg once said, “Everything in the future is a wave; everything in the past is a particle.” It has also been said that between release and detection particles behave like waves.
Wave-particle duality, a strange dichotomous co-dependency, was first recognized as a permanent feature of modern nanoscience when Niels Bohr proclaimed the complementarity principle as the corner stone of the Copenhagen interpretation of quantum theory. This scientific dogma states, among other things, that there will be no future resolution of the cognitive dissonance that results from analyses that require, at root level, the use of irreconcilable concepts such as wave and particle.
In what follows it will be shown that wave-particle duality leads naturally to other conjugate relationships between traditional physical variables such as position and momentum, and energy and time. The vehicle for this extension will turn out to be the Fourier transform.
To reason mathematically about wave behavior requires a wave function. The one-dimensional, time-independent plane wave expression for a free particle is suitable for this purpose.
\[
\exp \left(i 2 \pi \frac{x}{\lambda}\right)
\nonumber \]
We see that this expression contains the basics of wave-particle duality; x represents position, a particle characteristic, and \(\lambda\) represents wave behavior. Substitution of the de Broglie equation for \(\lambda\) yields one of the most important mathematical functions in quantum mechanics.
\[
\exp \left(\frac{i p x}{h}\right)
\nonumber \]
By convention this function is called the momentum eigenfunction in the coordinate representation. We express this in Dirac notation as follows (the normalization constant is ignored for the time being).
\[
\langle x | p\rangle=\exp \left(\frac{i p x}{\hbar}\right)
\nonumber \]
Its complex conjugate is the position eigenfunction in the momentum representation.
\[
\langle p | x\rangle=\langle x | p\rangle^{*}=\exp \left(\frac{-i p x}{\hbar}\right)
\nonumber \]
Both expressions are also simple examples of Fourier transforms. They are dictionaries for translating between two different languages or representations. A rudimentary graphical illustration of this ability to translate also provides a concise illustration of the uncertainty principle. (See The Emperor’s New Mind, by Roger Penrrose, page 246.)
A quon (“A quon is any entity, no matter how immense, that exhibits both wave and particle aspects in the peculiar quantum manner.” Quantum Reality by Nick Herbert page 64.) with a precise position is represented by a Dirac delta function in coordinate space and a helix in momentum space. If the position is known exactly, the momentum is completely unknown because \(|\langle p | x_{1}\rangle|^{2}\) is a constant for all values of the momentum. All momentum values have the same probability of being observed.
A quon has position \(x_{1} : | x_{1} \rangle\)
\[\begin{matrix} \text{Coordinate space} & \Leftrightarrow & \text{Momentum space} \\ \langle x | x_{1}\rangle=\delta\left(x-x_{1}\right) & \; & \langle p | x_{1}\rangle=\exp \left(-\frac{i p x_{1}}{\hbar}\right) \end{matrix} \nonumber \]
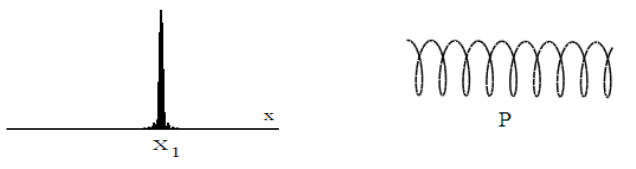
These rudimentary examples of the use of the Fourier transform in quantum mechanics involve infinitesimal points in coordinate and momentum space. To employ the Fourier transform for objects of finite dimensions requires integration over the spatial or momentum dimensions.
For example, suppose we ask what the pattern of diffracted light on a distant screen would look like if a light source illuminated a mask with a single small circular aperture. This, of course, yields the well-known Airy diffraction pattern, which is nothing more than the Fourier transform of the coordinate wave function (the circular aperture) into momentum space. The Airy pattern calculation is given in the following tutorial, along with illustrations of how the radius of the hole illustrates the uncertainty principle.
Calculating the Airy Diffraction Pattern
The Airy diffraction pattern is created by illuminating a screen containing a circular hole with photons. The experiment can be performed with weak sources such that there is only one photon interacting with the screen at a time. This photon-screen interaction constitutes a position measurement.

The position wave function has a constant amplitude within the area of the hole and is shown to be normalized.
\[
\Psi(x, y) :=\frac{1}{\sqrt{\pi \cdot R^{2}}} \quad \mathrm{R}^{2}=x^{2}+y^{2} \quad \int_{-R}^{\mathrm{R}} \int_{-\sqrt{\mathrm{R}^{2}-\mathrm{x}^{2}}}^{\sqrt{\mathrm{R}^{2}-\mathrm{x}^{2}}} \Psi(\mathrm{x}, \mathrm{y})^{2} \mathrm{dy} \mathrm{d} \mathrm{x}=1
\nonumber \]
The Airy diffraction pattern is the Fourier transform of the position wave function into the momentum representation. In other words, the interference pattern at the detection screen actually represents a momentum measurement. The following calculations are carried out in atomic units using a hole radius of 0.2.
Hole radius: \(R :=0.2\)
Calculate the Airy diffraction pattern:
\[
\Delta :=100 \quad \mathrm{N} :=80 \quad \mathrm{j} :=0 \ldots \mathrm{N} \quad \mathrm{p}_{\mathrm{x}_{\mathrm{j}}}=-\Delta+\frac{2 \cdot \Delta \cdot \mathrm{j}}{\mathrm{N}} \quad \mathrm{k} :=0 \ldots \mathrm{N} \quad \quad \mathrm{p}_{\mathrm{y}_{k}} :=-\Delta+\frac{2 \cdot \Delta \cdot \mathrm{k}}{\mathrm{N}}
\nonumber \]
\[
\Phi\left(\mathrm{p}_{\mathrm{x}}, \mathrm{p}_{\mathrm{y}}\right) :=\frac{1}{\pi} \cdot \int_{-\mathrm{R}}^{\mathrm{R}} \int_{-\sqrt{\mathrm{R}^{2}-\mathrm{x}^{2}}^{2}}^{\sqrt{\mathrm{R}^{2}-\mathrm{x}^{2}}^{2}} \frac{1}{\sqrt{\pi \cdot \mathrm{R}^{2}}} \cdot \exp \left(-\mathrm{i} \cdot \mathrm{p}_{\mathrm{x}} \cdot \mathrm{x}\right) \cdot \exp \left(-\mathrm{i} \cdot \mathrm{p}_{\mathrm{y}} \cdot \mathrm{y}\right)dy\;dx \quad \mathrm{P}_{\mathrm{j}, \mathrm{k}} :=\left(|\Phi\mathrm{p}_{\mathrm{x}_{\mathrm{j}}}, \mathrm{p}_{\mathrm{y}_{k}})|\right)^{2}
\nonumber \]
Display the Airy diffraction pattern.
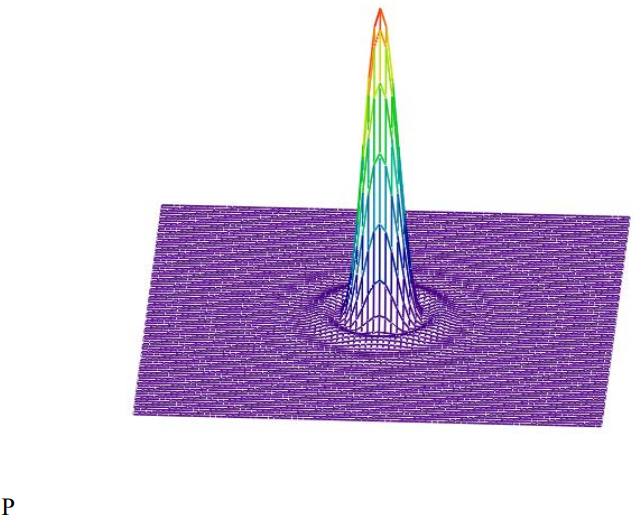
Truncating the high intensity central disk provides a better picture of the outer maxima and minima.
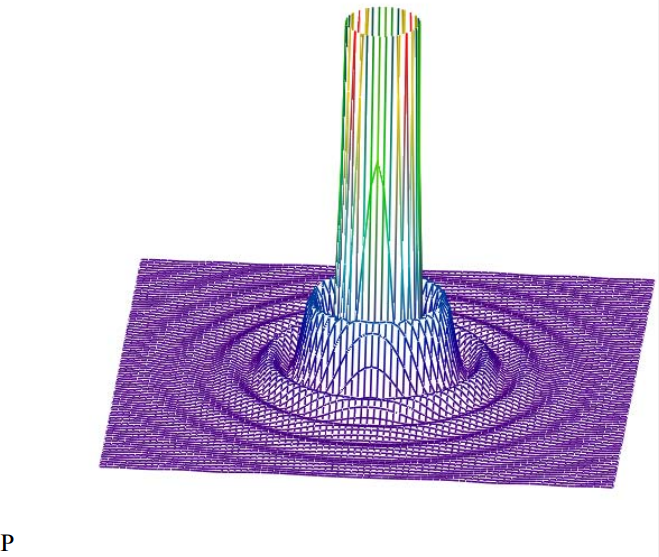
Examining a radial slice of the Airy diffraction pattern provides a simple illustration of the uncertainty principle. Assume that the position uncertainty is given by the diameter of the hole and that the momentum uncertainty is given by the momentum range of the central disk.
\[
\mathrm{py} :=0 \quad \mathrm{px} :=-100,-99 \ldots 100 \quad \Phi(\mathrm{px}, \mathrm{py}, \mathrm{R}) :=\frac{1}{\pi} \cdot \int_{-\mathrm{R}}^{\mathrm{R}} \int_{-\sqrt{\mathrm{R}^{2}-\mathrm{x}^{2}}}^{\sqrt{\mathrm{R}^{2}-\mathrm{x}^{2}}} \frac{1}{\sqrt{\pi \cdot \mathrm{R}^{2}}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \mathrm{x} \cdot \mathrm{x}) \cdot \exp (-\mathrm{i} \cdot \mathrm{py} \cdot \mathrm{y})dy\;dx
\nonumber \]
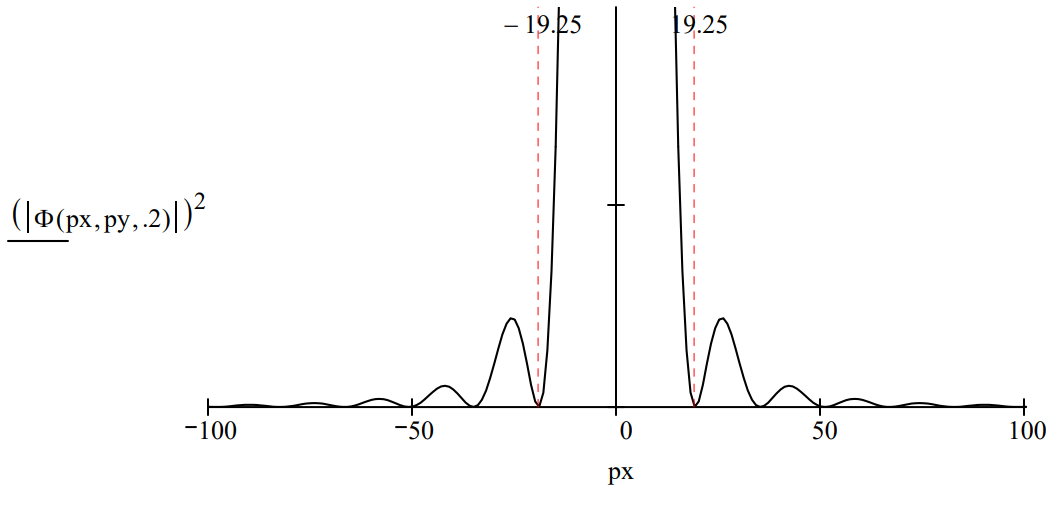
For a diameter of 0.4 the position-momentum uncertainty product is:
\[0.4 \cdot 38.5 = 15.4 \nonumber \]
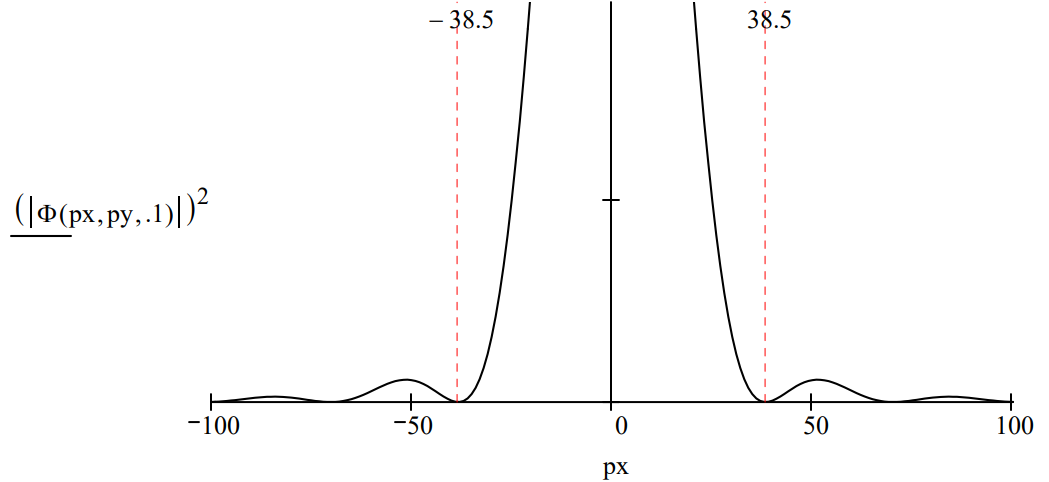
For a diameter of 0.2 the position-momentum uncertainty product is:
\[0.2 \cdot 77.0 = 15.4 \nonumber \]
The reciprocal relationship between the uncertainty in position and momentum is clearly revealed in this example.
The Double-Slit Experiment

Coordinate wave function:
\[
| \Psi \rangle=\frac{1}{\sqrt{2}}[ |x_{1}\rangle+| x_{2} \rangle ]
\nonumber \]
Momentum wave function for infinitesimally thin slits:
\[
\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle]=\frac{1}{2 \sqrt{\pi}}\left[\exp \left(-\frac{i p x_{1}}{\hbar}\right)+\exp \left(-\frac{i p x_{2}}{\hbar}\right)\right]
\nonumber \]
Position of first slit:
\[x_{1} : = 0 \nonumber \]
Position of second slit:
\[x_{2} : = 1 \nonumber \]
Momentum wave function for finite slits:
\[\Psi (p) : = \frac{\int_{\mathrm{x}_{1}-\frac{\delta}{2}}^{\mathrm{x}_{1}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x} +\int_{\mathrm{x}_{2}-\frac{\delta}{2}}^{\mathrm{x}_{2}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x}}{\sqrt{2}} \nonumber \]
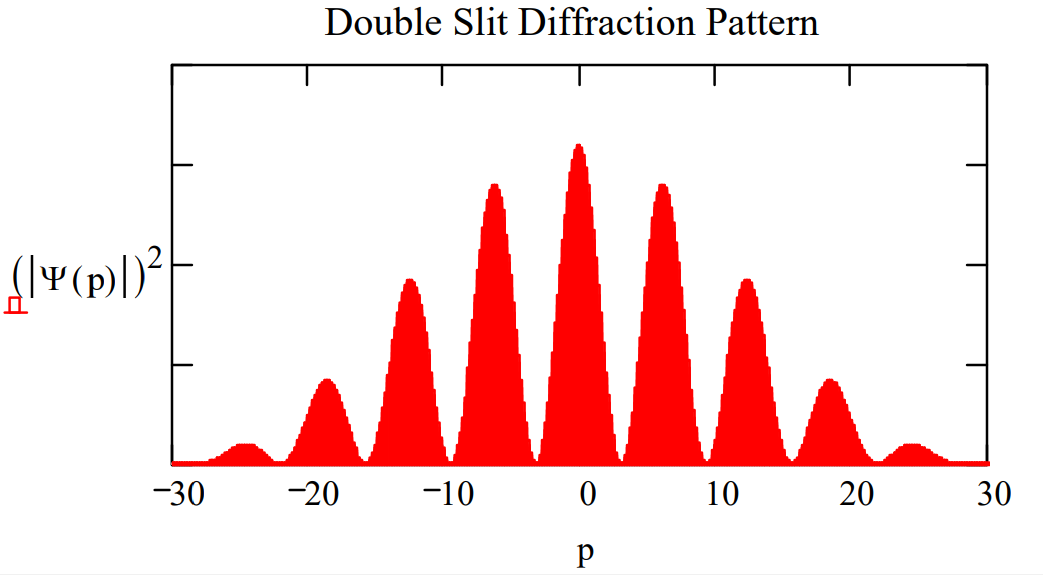
According to the Encyclopedia Britannica, Fresnel and Arago “using an apparatus based on Young’s experiment” observed that “two beams polarized in mutually parallel planes never yield fringes.” In the following tutorial this phenomenon is examined from the quantum mechanical perspective and a critique of the concept of the quantum eraser is provided.
Which Path Information and the Quantum Eraser
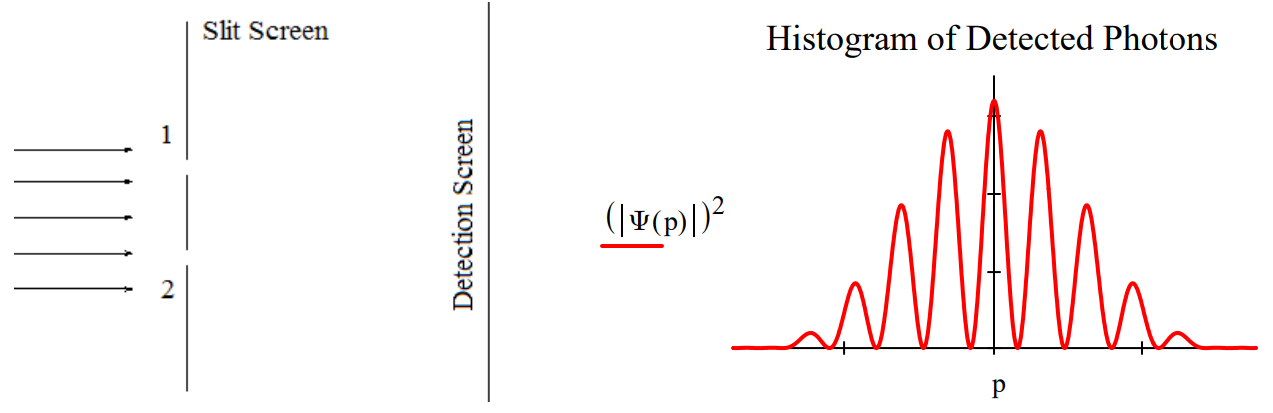
This tutorial examines the real reason which‐path information destroys the double‐slit diffraction pattern and how the so‐called ʺquantum eraserʺ restores it. The wave function for a photon illuminating the slit screen is written as a superposition of the photon being present at both slits simultaneously. The double‐slit diffraction pattern is calculated by projecting this superposition into momentum space. This is a Fourier transform for which the mathematical details can be found in the Appendix.
\[
| \Psi \rangle=\frac{1}{\sqrt{2}}[ |x_{1}\rangle+| x_{2} \rangle ] \qquad \Psi(p)=\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle]
\nonumber \]
Attaching polarizers to the slits creates an entangled superposition of the photon being at slit 1 with vertical polarization and at slit 2 with horizontal polarization. This leads to the following momentum distribution at the detection screen. The interference fringes have disappeared leaving a single‐slit diffraction pattern.
\[
| \Psi^{\prime} \rangle=\frac{1}{\sqrt{2}}[ |x_{1}\rangle | V \rangle+| x_{2} \rangle | H \rangle ] \qquad \Psi^{\prime}(p)=\langle p | \Psi^{\prime}\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle | V\rangle+\langle p | x_{2}\rangle | H \rangle ]
\nonumber \]
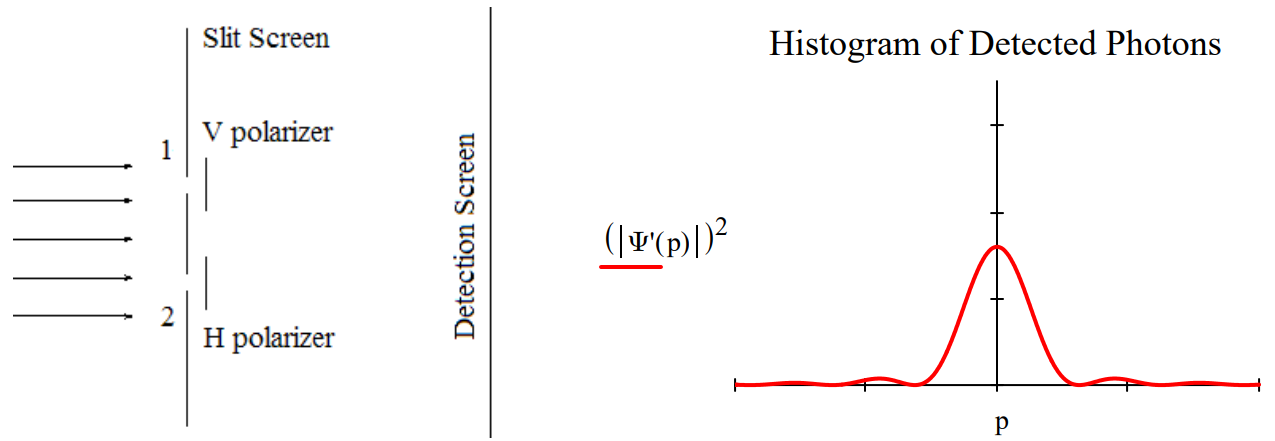
The usual explanation for this effect is that it is now possible to know which slit the photons went through, and that such knowledge destroys the interference fringes because the photons are no longer in a superposition of passing through both slits, but rather a mixture of passing through one slit or the other.
However, a better explanation is that the superposition persists with orthogonal polarization tags, and because of this the interference (cross) terms in the momentum distribution, \(\left|\Psi^{\prime}(p)\right|^{2}\), vanish leaving a pattern at the detection screen which is the sum of two single‐slit diffraction patterns, one from the upper slit and the other from the lower slit.
That this is a reasonable interpretation is confirmed when a so‐called quantum eraser, a polarizer (D) rotated clockwise by 45 degrees relative to the vertical, is placed before the detection screen.
\[
\Psi^{\prime \prime}(p)=\langle D | \Psi^{\prime}(p)\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle\langle D | V\rangle+\langle p | x_{2}\rangle\langle D | H\rangle]=\frac{1}{2}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle]
\nonumber \]

The diagonal polarizer is called a quantum eraser because it appears to restore the interference pattern lost because of the which‐path information provided by the V/H polarizers. However, it is clear from this analysis that the diagonal polarizer doesnʹt actually erase, it simply passes the diagonal component of \(| \Psi^{'} \rangle\) which then shows an attenuated (by half) version of the original interference pattern produced by \(| \Psi \rangle\).
Placing an anti‐diagonal polarizer (rotated counterclockwise by 45 degrees relative to the vertical) before the detection screen causes a 180 degree phase shift in the restored interference pattern.
\[
\Psi^{\prime \prime}(p)=\langle A | \Psi^{\prime}(p)\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle\langle A | V\rangle+\langle p | x_{2}\rangle\langle A | H\rangle]=\frac{1}{2}[\langle p | x_{1}\rangle-\langle p | x_{2}\rangle]
\nonumber \]
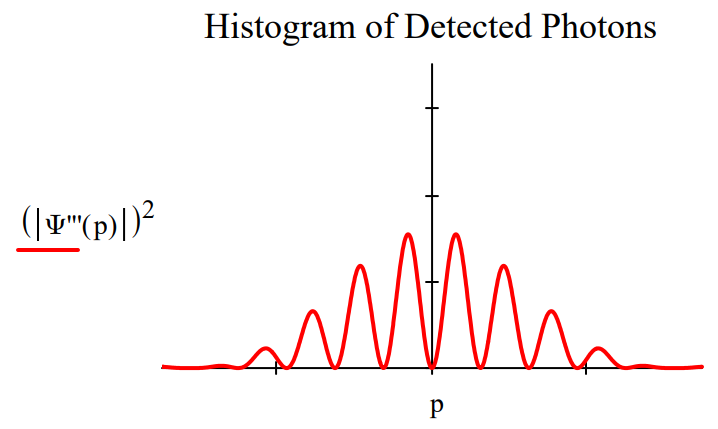
This phase shift is inconsistent with any straightforward explanation based on the concept of erasure of which‐path information. Erasure implies removal of which‐path information. If which‐path information has been removed shouldnʹt the original interference pattern be restored without a phase shift?
- Appendix:
-
The V/H polarization which‐path tags and the D/A polarization ʺerasersʺ in vector format:
\[
| \mathrm{V} \rangle=\left( \begin{array}{l}{1} \\ {0}\end{array}\right) \quad | \mathrm{H} \rangle=\left( \begin{array}{l}{0} \\ {1}\end{array}\right) \quad | \mathrm{D} \rangle=\frac{1}{\sqrt{2}} \left( \begin{array}{l}{1} \\ {1}\end{array}\right) \quad | \mathrm{A} \rangle=\frac{1}{\sqrt{2}} \left( \begin{array}{c}{1} \\ {-1}\end{array}\right) \\ \langle\mathrm{D} | \mathrm{V}\rangle=\langle\mathrm{D} | \mathrm{H}\rangle=\langle\mathrm{A} | \mathrm{V}\rangle=\frac{1}{\sqrt{2}}\quad \langle\mathrm{A} | \mathrm{H}\rangle=-\frac{1}{\sqrt{2}}
\nonumber \]For infinitesimally thin slits the momentum‐space wave function is,
\[
\Psi(p)=\langle p | \Psi\rangle=\frac{1}{\sqrt{2}}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle]=\frac{1}{\sqrt{2}}\left[\frac{1}{\sqrt{2 \pi}} \exp \left(-i p x_{1}\right)+\frac{1}{\sqrt{2 \pi}} \exp \left(-i p x_{2}\right)\right]
\nonumber \]Assuming a slit width \(\delta\) the calculations of \(\Psi(p), \Psi^{ʹ}(p), \Psi^{ʹʹ}(p)\) and \(\Psi^{ʹʹʹ}(p)\) are carried out as follows:
Position of first slit: \(x_{1} \equiv 0\) Position of second slit: \(x_{2} \equiv 1\) Slit width: \(\delta \equiv 0.2\) \[
\Psi(p)\equiv\frac{1}{\sqrt{2}} \cdot\left(\int_{x_{1}-\frac{\delta}{2}}^{x_{1}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x+\int_{x_{2}-\frac{\delta}{2}}^{x_{2}+\frac{\delta}{2}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-i \cdot p \cdot x) \cdot \frac{1}{\sqrt{\delta}} d x\right]
\nonumber \]For \(\Psi^{ʹ}(p)\) the V/H polarization which‐path tags are added to the two terms of \(\Psi (p)\)
\[
\Psi^{\prime}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \cdot\left[\int_{\mathrm{x}_{1}-\frac{\delta}{2}}^{\mathrm{\mathrm{x}_{1}+\frac{\delta}{2}}} \frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x} \cdot \left( \begin{array}{l}{1} \\ {0}\end{array}\right)+\int_{x_{2}-\frac{\delta}{2}}^{x_{2}+\frac{\delta}{2}}\frac{1}{\sqrt{2 \cdot \pi}} \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{x}) \cdot \frac{1}{\sqrt{\delta}} \mathrm{d} \mathrm{x} \cdot \left( \begin{array}{l}{0} \\ {1}\end{array}\right) \right]
\nonumber \]\(\Psi^{ʹʹ}(p)\) is the projection of \(\Psi^{ʹ}(p)\) onto a diagonal polarizer \(\langle D |\).
\[
\Psi^{\prime \prime}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \cdot \left( \begin{array}{l}{1} \\ {1}\end{array}\right)^{\mathrm{T}} \cdot \Psi^{\prime}(\mathrm{p})
\nonumber \]\(\Psi^{ʹʹʹ}(p)\) is the projection of \(\Psi^{ʹ}(p)\) onto an anti‐diagonal polarizer \(\langle A |\).
\[
\Psi^{\prime \prime \prime}(\mathrm{p}) \equiv \frac{1}{\sqrt{2}} \cdot \left( \begin{array}{c}{1} \\ {-1}\end{array}\right)^{\mathrm{T}} \cdot \Psi^{\prime}(\mathrm{p})
\nonumber \]Rewriting \(\Psi^{ʹ}(p)\) in terms of \(| D \rangle\) and \(| A \rangle\) clearly shows the origin of the phase difference between the \(\left(|\Psi^{\prime \prime}(\mathrm{p})|\right)^{2}\) and \(\left(|\Psi^{\prime \prime \prime}(\mathrm{p})|\right)^{2}\) interference patterns.
\[
\Psi^{\prime}(p)=\langle p | \Psi^{\prime}\rangle=\frac{1}{2}[\langle p | x_{1}\rangle+\langle p | x_{2}\rangle) | D \rangle+(\langle p | x_{1}\rangle-\langle p | x_{2}\rangle) | A \rangle ]
\nonumber \]

