1.100: Analysis of the Stern-Gerlach Experiment
- Page ID
- 158606
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The purpose of this tutorial is to analyze the Stern-Gerlach experiment using matrix mechanics. The figure below is taken (and modified) from Thomas Engel's text, Quantum Chemistry & Spectroscopy.
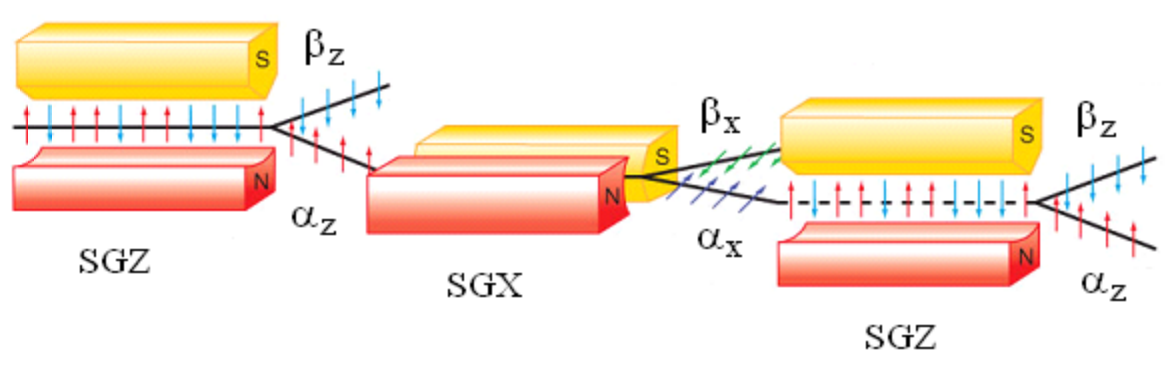
Silver atoms are deflected by an inhomogeneous magnetic field because of the two-valued magnetic moment associated with their unpaired 5s electron ([Kr]5s14d10). The beam of silver atoms entering the Stern-Gerlach magnet oriented in the z-direction (SGZ) on the left is unpolarized. This means it is a mixture of randomly spin-polarized Ag atoms. As such, it is impossible to write a quantum mechanical wavefunction for this initial state.
This situation is exactly analogous to the three-polarizer demonstration described in a previous tutorial. Light emerging from an incadescent light bulb is unpolarized, a mixture of all possible polarization angles, so we can't write a wave function for it. The first Stern-Gerlach magnet plays the same role as the first polarizer, it forces the Ag atoms into one of measurement eigenstates - spin-up or spin-down in the z-direction. The only difference is that in the three-polarizer demonstration only one state was created - vertical polarization. Both demonstrations illustrate an important quantum mechanical postulate - the only values that are observed in a measurement are the eigenvalues of the measurement operator.
To continue with the analysis of the Stern-Gerlach demonstration we need vectors to represent the various spin states of the Ag atoms. We will restrict our attention to the x- and z- spin directions, although the spin states for the y-direction are also available.
Spin Eigenfunctions
| Spin-up in the z-direction: | \(\alpha_{Z} :=\left(\begin{array}{l}{1} \\ {0}\end{array}\right)\) |
| Spin-down in the z-direction: | \(\beta_{\mathrm{z}} :=\left(\begin{array}{l}{0} \\ {1}\end{array}\right)\) |
| Spin-up in the x-direction: | \(\alpha_{\mathrm{x}} :=\frac{1}{\sqrt{2}} \cdot\left(\begin{array}{l}{1} \\ {1}\end{array}\right)\) |
| Spin-down in the x-direction: | \(\beta_{\mathrm{x}} :=\frac{1}{\sqrt{2}} \cdot\left(\begin{array}{c}{1} \\ {-1}\end{array}\right)\) |
After the SGZ magnet, the spin-up beam (deflected toward the magnet's north pole) enters a magnet oriented in the x-direction, SGX. The \(\alpha_{z}\) beam splits into \(\alpha_{x}\) and \(\beta_{x}\) beams of equal intensity. This is because it is a superposition of the x-direction spin eigenstates as shown below.
\[
\frac{1}{\sqrt{2}} \cdot\left[\frac{1}{\sqrt{2}} \cdot\left(\begin{array}{c}{1} \\ {1}\end{array}\right)+\frac{1}{\sqrt{2}} \cdot\left(\begin{array}{c}{1} \\ {-1}\end{array}\right)\right] \rightarrow\left(\begin{array}{c}{1} \\ {0}\end{array}\right) \qquad \frac{1}{\sqrt{2}} \cdot\left(\alpha_{\mathrm{x}}+\beta_{\mathrm{x}}\right) \rightarrow\left(\begin{array}{c}{1} \\ {0}\end{array}\right)
\nonumber \]
Next the \(\alpha_{x}\) beam is directed toward a second SGZ magnet and splits into two equal \(\alpha_{z}\) and \(\beta_{z}\) beams. This happens because \(\alpha_{x}\) is a superposition of the \(\alpha_{z}\) and \(\beta_{z}\) spin states.
\[
\frac{1}{\sqrt{2}} \cdot\left[\left(\begin{array}{l}{1} \\ {0}\end{array}\right)+\left(\begin{array}{l}{0} \\ {1}\end{array}\right)\right]=\left(\begin{array}{l}{0.707} \\ {0.707}\end{array}\right) \qquad \frac{1}{\sqrt{2}} \cdot\left(\alpha_{\mathrm{z}}+\beta_{\mathrm{z}}\right)=\left(\begin{array}{c}{0.707} \\ {0.707}\end{array}\right)
\nonumber \]
Operators
We can also use the Pauli operators (in units of h/4\(pi\)) to analyze this experiment. The matrix operators associated with the two Stern-Gelach magnets are shown below.
SGZ operator:
\[
\mathrm{SGZ} :=\left(\begin{array}{cc}{1} & {0} \\ {0} & {-1}\end{array}\right)
\nonumber \]
SGX operator:
\[
\operatorname{SGX} :=\left(\begin{array}{ll}{0} & {1} \\ {1} & {0}\end{array}\right)
\nonumber \]
The spin states \(\alpha_{z}\) and \(\beta_{z}\) are eigenfunctions of the SGZ operator with eigenvalues +1 and -1, respectively:
\[
S G Z \cdot \alpha_{z}=\alpha_{z} \qquad \operatorname{SGZ} \cdot \alpha_{z}=\left(\begin{array}{l}{1} \\ {0}\end{array}\right)
\nonumber \]
\[
S G Z \cdot \beta_{z}=-\beta_{z} \qquad \operatorname{SGZ} \cdot \beta_{\mathrm{z}}=\left(\begin{array}{c}{0} \\ {-1}\end{array}\right)
\nonumber \]
The spin states \(\alpha_{x}\) and \(\beta_{x}\) are eigenfunctions of the SGX operator with eigenvalues +1 and -1, respectively:
\[
S G X \cdot \alpha_{x}=\alpha_{x} \qquad \mathrm{SGX} \cdot \alpha_{\mathrm{x}}=\left(\begin{array}{c}{0.707} \\ {0.707}\end{array}\right)
\nonumber \]
\[
S G X \cdot \beta_{x}=-\beta_{x} \qquad \mathrm{SGX} \cdot \beta_{\mathrm{x}}=\left(\begin{array}{c}{-0.707} \\ {0.707}\end{array}\right)
\nonumber \]
The spin states \(\alpha_{x}\) and \(\beta_{x}\) are not eigenfunctions of the SGZ operator as is shown below.
\[
S G Z \cdot \alpha_{x}=\beta_{x} \qquad \mathrm{SGZ} \cdot \alpha_{\mathrm{x}}=\left(\begin{array}{c}{0.707} \\ {-0.707}\end{array}\right)
\nonumber \]
\[
S G Z \cdot \beta_{x}=\alpha_{x} \qquad \mathrm{SGZ} \cdot \beta_{\mathrm{x}}=\left(\begin{array}{c}{0.707} \\ {0.707}\end{array}\right)
\nonumber \]
And, of course, the spin states \(\alpha_{z}\) and \(\beta_{z}\) are not eigenfunctions of the SGX operator as is shown below.
\[
S G X \cdot \alpha_{z}=\beta_{z} \qquad \mathrm{SGX} \cdot \alpha_{\mathrm{z}}=\left(\begin{array}{l}{0} \\ {1}\end{array}\right)
\nonumber \]
\[
S G X \cdot \beta_{z}=\alpha_{z} \qquad \operatorname{SGX} \cdot \beta_{2}=\left(\begin{array}{l}{1} \\ {0}\end{array}\right)
\nonumber \]
The Predicted Results After the SGX Magnet
The probability that an \(\alpha_{z}\) Ag atom will emerge spin-up after passing through a SGX magnet:
\[
\left|\left\langle\alpha_{x}|S G X| \alpha_{z}\right\rangle\right|^{2}=1 / 2 \qquad\left(|\alpha_{x}^{\mathrm{T}} \cdot \operatorname{SGX} \cdot \alpha_{2}|\right)^{2} \rightarrow \frac{1}{2}
\nonumber \]
The probability that an \(\alpha_{z}\) Ag atom will emerge spin-down after passing through a SGX magnet:
\[
\left|\left\langle\beta_{x}|\operatorname{SGX}| \alpha_{z}\right\rangle\right|^{2}=1 / 2 \qquad\left(|\beta_{\mathrm{x}}^{\mathrm{T}} \cdot \operatorname{SGX} \cdot \alpha_{2}|\right)^{2} \rightarrow \frac{1}{2}
\nonumber \]
The Predicted Results After the Final SGZ Magnet
The probability that an \(\alpha_{x}\) Ag atom will emerge spin-up after passing through a SGZ magnet:
\[
\left|\left\langle\alpha_{z}|\operatorname{SGZ}| \alpha_{x}\right\rangle\right|^{2}=1 / 2 \qquad\left(|\alpha_{2}^{\mathrm{T}} \cdot \operatorname{SGZ} \cdot \alpha_{\mathrm{x}}|\right)^{2} \rightarrow \frac{1}{2}
\nonumber \]
The probability that an \(\alpha_{x}\) Ag atom will emerge spin-down after passing through a SGZ magnet:
\[
\left|\left\langle\beta_{z}|\operatorname{SGZ}| \alpha_{x}\right\rangle\right|^{2}=1 / 2 \qquad\left(|\beta_{2}^{\mathrm{T}} \cdot \operatorname{SGZ} \cdot \alpha_{\mathrm{x}}|\right)^{2} \rightarrow \frac{1}{2}
\nonumber \]
The Predicted Results for the First SGZ Magnet
Now we deal with the most difficult part of the analysis. How does quantum mechanics predict what will happen when an unpolarized spin beam encounters the initial SGZ magnet. As mention earlier, an unpolarized spin beam is a mixture of all possible spin polarizations. We proceed by introducing the density operator, which is a more general quantum mechanical construct that can be used to represent both pure states and mixtures, as shown below.
\[
\hat{\rho}_{\text {pure}}=|\Psi\rangle\langle\Psi| \qquad \hat{\rho}_{m i x e d}=\sum p_{i}\left|\Psi_{i}\right\rangle\left\langle\Psi_{i}\right|
\nonumber \]
In the equation on the right, pi is the fraction of the mixture in the state \(\Psi_{i}\). It is not difficult to elucidate the origin of the density operator and its utility in quantum mechanical calculations. The expectation value for a pure state \(\Psi\) for the measurement operator A is traditionally written as follows.
\[
\langle A\rangle=\langle\Psi|\hat{A}| \Psi\rangle
\nonumber \]
Expansion of \(\Psi\) in the eigenfunctions of the measurement operator, followed by rearrangement of the brackets yields the calculation of the expectation value of A in terms of the product of density operator and the measurement operator, A.
\[
\langle A\rangle=\langle\Psi|\hat{A}| \Psi\rangle=\sum\langle\Psi|\hat{A}| a\rangle\langle a | \Psi\rangle=\sum_{d}\langle a | \Psi\rangle\langle\Psi|\hat{A}| a\rangle=\sum\langle a|\hat{\rho} \hat{A}| a\rangle=\operatorname{Trace}(\hat{\rho} \hat{A})
\nonumber \]
We now show that the traditional method and the method using the trace function give the same result for the z-direction spin eigenfunctions.
\[
\begin{matrix} \alpha_{\mathrm{z}}^{\mathrm{T}} \cdot \mathrm{SGZ} \cdot \alpha_{\mathrm{z}}=1 & \operatorname{tr}\left(\alpha_{\mathrm{z}} \cdot \alpha_{\mathrm{z}}^{\mathrm{T}} \cdot \operatorname{SGZ}\right)=1 \\ \beta_{\mathrm{Z}}^{\mathrm{T}} \cdot \mathrm{SGZ} \cdot \beta_{\mathrm{z}}=-1 & \operatorname{tr}\left(\beta_{\mathrm{Z}} \cdot \beta_{\mathrm{Z}}^{\mathrm{T}} \cdot \mathrm{SGZ}\right)=-1 \end{matrix}
\nonumber \]
An unpolarized beam can be written as a 50-50 mixture of any of the orthogonal spin eigenfunctions - \(\alpha_{z}\) and \(\beta_{z}\), or \(\alpha_{x}\) and \(\beta_{x}\), or \(\alpha_{y}\) and \(\beta_{y}\). Thus, according to the previous definition the density operator for an unpolarized spin beam is as follows.
\[
\hat{\rho}_{\operatorname{mix}}=\frac{1}{2}|\alpha_{z}\rangle\langle\alpha_{z}|+\frac{1}{2}| \beta_{z}\rangle\langle\beta_{z}|=\frac{1}{2}| \alpha_{x}\rangle\langle\alpha_{x}|+\frac{1}{2}| \beta_{x}\rangle\langle\beta_{x}|=\frac{1}{2}| \alpha_{y}\rangle\langle\alpha_{y}|+\frac{1}{2}| \beta_{y}\rangle\langle\beta_{y}|
\nonumber \]
Fifty percent of the silver atoms are deflected toward the north pole (\(\alpha_{z}\), eigenvalue +1) and fifty percent toward the south pole (\(\beta_{z}\), eigenvalue -1). Therefore, the expectation value should be zero as is calculated below using both z- and x- spin directions.
\[
\operatorname{tr}\left[\left(\frac{1}{2} \cdot \alpha_{2} \cdot \alpha_{2}^{T}+\frac{1}{2} \cdot \beta_{z} \cdot \beta_{z}^{T}\right) \cdot \operatorname{SGZ}\right]=0 \qquad \operatorname{tr}\left[\left(\frac{1}{2} \cdot \alpha_{x} \cdot \alpha_{x}^{T}+\frac{1}{2} \cdot \beta_{x} \cdot \beta_{x}^{T}\right) \cdot \operatorname{SGZ}\right]=0
\nonumber \]
An equivalent method of obtaining the same result is shown below.
\[
\frac{1}{2} \cdot \alpha_{z}^{T} \cdot \operatorname{SGZ} \cdot \alpha_{z}+\frac{1}{2} \cdot \beta_{z}^{T} \cdot \operatorname{SGZ} \cdot \beta_{z}=0 \qquad \frac{1}{2} \cdot \alpha_{z}^{T} \cdot \operatorname{SGZ} \cdot \alpha_{z}+\frac{1}{2} \cdot \beta_{z}^{T} \cdot \operatorname{SGZ} \cdot \beta_{z}=0
\nonumber \]

