1.82: The Position‐Momentum Uncertainty Relation in the Hydrogen Atom

The hydrogen atom coordinate and momentum wave functions can be used to illustrate the uncertainty relation involving position and momentum.

The 1s wave function is used to calculate the average distance of the electron from the nucleus.

\[
\Psi_{1 s}(\mathrm{r}) :=\frac{1}{\sqrt{\pi}} \cdot \exp (-\mathrm{r}) \qquad \mathrm{r}_{1 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{r} \cdot \Psi_{1 \mathrm{s}}(\mathrm{r})^{2} \cdot 4 \cdot \pi \cdot \mathrm{r}^{2} \mathrm{d} \mathrm{r} \qquad r_{1 s}=1.500
\nonumber \]

The Fourier transform of the 1s wave function yields the momentum wave function. The momentum wave function is used to calculate the average magnitude of the electron momentum.

\[
\Phi_{1 \mathrm{s}}(\mathrm{p}) :=\frac{1}{\sqrt{8 \cdot \pi^{3}}} \cdot \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2 \cdot \pi} \Psi_{\mathrm{ls}}(\mathrm{r}) \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \mathrm{r} \cdot \cos (\theta)) \cdot \mathrm{r}^{2} \cdot \sin (\theta) \mathrm{d} \phi \mathrm{d} \theta \mathrm{dr} \rightarrow 2 \cdot \frac{2^{\frac{1}{2}}}{\pi \cdot[(-1)+\mathrm{i} \cdot \mathrm{p}]^{2} \cdot(1+\mathrm{i} \cdot \mathrm{p})^{2}} \\ \mathrm{p}_{1 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{p} \cdot\left(\left|\Phi_{1 \mathrm{s}}(\mathrm{p})\right|\right)^{2} \cdot 4 \cdot \pi \cdot \mathrm{p}^{2} \mathrm{d} \mathrm{p} \qquad \mathrm{p}_{1 \mathrm{s}}=0.849
\nonumber \]

The 2s wave function is used to calculate the average distance of the electron from the nucleus.

\[
\Psi_{2 s}(r) :=\frac{1}{\sqrt{32 \cdot \pi}} \cdot(2-r) \cdot \exp \left(-\frac{r}{2}\right) \qquad \mathrm{r}_{2 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{r} \cdot \Psi_{2 \mathrm{s}}(\mathrm{r})^{2} \cdot 4 \cdot \pi \cdot \mathrm{r}^{2} \mathrm{dr} \qquad \mathrm{r}_{2 \mathrm{s}}=6.000
\nonumber \]

The Fourier transform of the 2s wave function yields the momentum wave function. The momentum wave function is used to calculate the average magnitude of the electron momentum.

\[
\Phi_{2 \mathrm{s}}(\mathrm{p}) :=\frac{1}{\sqrt{8 \cdot \pi^{3}}} \cdot \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2 \cdot \pi} \Psi_{2 \mathrm{s}}(\mathrm{r}) \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \cos (\theta)) \cdot \mathrm{r}^{2} \cdot \sin (\theta) \mathrm{d} \phi \mathrm{d} \theta \mathrm{dr} \rightarrow \frac{-16}{\pi} \cdot \frac{(-1)+4 \cdot p^{2}}{[(-1)+2 \cdot i \cdot p]^{3} \cdot(1+2 \cdot i \cdot p)^{3}} \\ \mathrm{p}_{2 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{p} \cdot\left(\left|\Phi_{2 \mathrm{s}}(\mathrm{p})\right|\right)^{2} \cdot 4 \cdot \pi \cdot \mathrm{p}^{2} \mathrm{d} \mathrm{p} \qquad \mathrm{p}_{2 \mathrm{s}}=0.340
\nonumber \]

The 3s wave function is used to calculate the average distance of the electron from the nucleus

\[
\Psi_{3 s}(\mathrm{r}) :=\frac{1}{81 \cdot \sqrt{3 \cdot \pi}} \cdot\left(27-18 \cdot \mathrm{r}+2 \cdot \mathrm{r}^{2}\right) \exp \left(\frac{-\mathrm{r}}{3}\right) \qquad r_{3 s} :=\int_{0}^{\infty} r \cdot \Psi_{3 s}(r)^{2} \cdot 4 \cdot \pi \cdot r^{2} d r \qquad r_{3 s}=13.500
\nonumber \]

The Fourier transform of the 3s wave function yields the momentum wave function. The momentum wave function is used to calculate the average magnitude of the electron momentum.

\[
\Phi_{3 \mathrm{s}}(\mathrm{p}) :=\frac{1}{\sqrt{8 \cdot \pi^{3}}} \cdot \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2 \cdot \pi} \Psi_{3 \mathrm{s}}(\mathrm{r}) \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \cos (\theta)) \cdot \mathrm{r}^{2} \cdot \sin (\theta) \mathrm{d} \phi \mathrm{d} \theta \mathrm{dr} \rightarrow 18 \cdot \frac{2^{2}}{\pi} \cdot 3^{\frac{1}{2}} \cdot \frac{1-30 \cdot \mathrm{p}^{2}+81 \cdot \mathrm{p}^{4}}{[(-1)+3 \cdot \mathrm{i} \cdot \mathrm{p}]^{4} \cdot(1+3 \cdot \mathrm{i} \cdot \mathrm{p})^{4}} \\ \mathrm{p}_{3 \mathrm{s}} :=\int_{0}^{\infty} \mathrm{p} \cdot\left(\left|\Phi_{3 s}(\mathrm{p})\right|\right)^{2} \cdot 4 \cdot \pi \cdot \mathrm{p}^{2} \mathrm{d} \mathrm{p} \qquad \mathrm{p}_{3 \mathrm{s}}=0.218
\nonumber \]

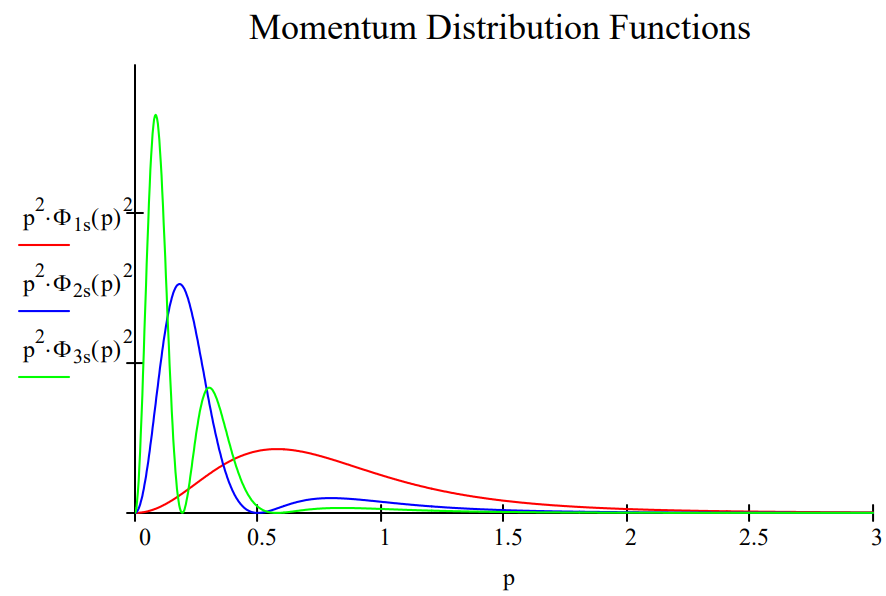
These results can be summarize in both tabular and graphical form.

\[
\left(\begin{array}{ccc}{\text { Orbital}} & \text{ AveragePosition} & \text{ AverageMomentum } \\ {1 \mathrm{s}} & {1.5} & {0.849} \\ {2 \mathrm{s}} & {6.0} & {0.340} \\ {3 \mathrm{s}} & {13.5} & {0.218}\end{array}\right)
\nonumber \]

The table shows that the average distance of the electron from the nucleus increases from 1s to 3s, indicating an increase in the uncertainty in the location of the electron. At the same time the average magnitude of electron momentum decreases from 1s to 3s, indicating a decrease in momentum uncertainty. The spatial and momentum distribution functions shown below illustrate this effect graphically.