1.81: Hydrogen Atom and Helium Ion Spatial and Momentum Distribution Functions Illustrate the Uncertainty Principle
- Page ID
- 157388
The uncertainty principle is revealed by a comparison of the coordinate and momentum wave functions for one‐electron species such as the hydrogen atom and the helium ion.
The coordinate 1s wave function for one‐electron species as a function of nuclear charge is given by the following function.
\[
\Psi(z, r) :=\sqrt{\frac{z^{3}}{\pi}} \cdot \exp (-z \cdot r)
\nonumber \]
The Fourier transform of the coordinate wave function yields the momentum wave function.
\[
\Phi(\mathrm{z}, \mathrm{p}) :=\frac{1}{\sqrt{8 \cdot \pi^{3}}} \cdot \int_{0}^{\infty} \int_{0}^{\pi} \int_{0}^{2 \cdot \pi} \Psi(\mathrm{z}, \mathrm{r}) \cdot \exp (-\mathrm{i} \cdot \mathrm{p} \cdot \cos (\theta)) \cdot \mathrm{r}^{2} \cdot \sin(\theta) \mathrm{d} \phi \mathrm{d} \theta \mathrm{dr} \Bigg|_{\text{assume,}\; z > 0}^{\text{simplify}} \rightarrow 2 \cdot \frac{2^{\frac{1}{2}}}{\pi} \cdot \frac{z^{\frac{5}{2}}}{z^{4}+2 \cdot z^{2} \cdot p^{2}+p^{4}}
\nonumber \]
Plots of the spatial and momentum radial distribution functions for the hydrogen atom (z=1) and helium ion (z=2) clearly illustrate the uncertainty principle.
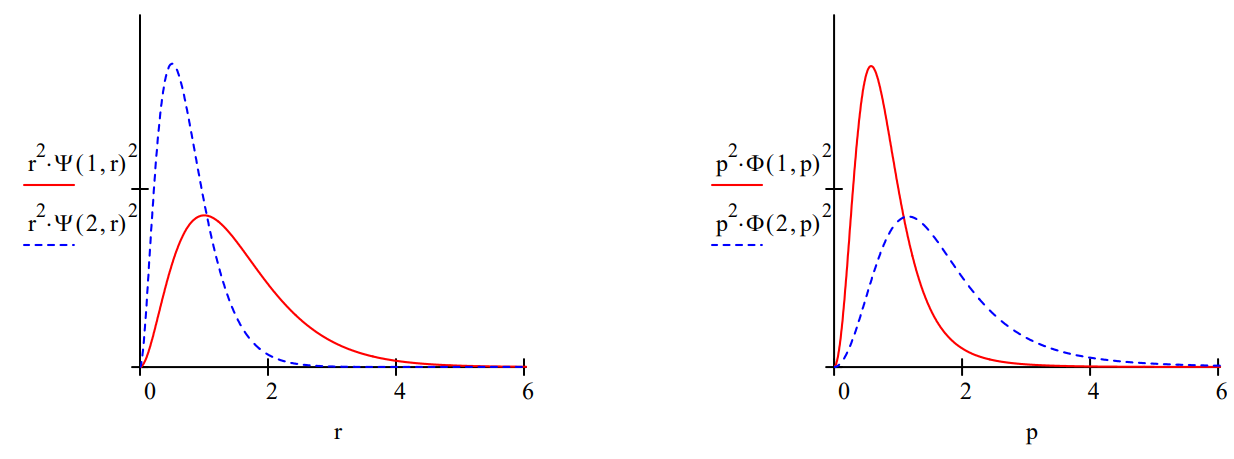
Relative to the hydrogen atom, the helium ionʹs coordinate distribution function is localized closer to the nucleus, meaning less uncertainty in electron position. Consequently, its momentum distribution is more delocalized than that for the hydrogen atom, meaning more uncertainty in electron momentum.

