21.2: The 3rd Law of Thermodynamics Puts Entropy on an Absolute Scale
- Page ID
- 14477
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)In the unlikely case that we have \(C_p\) data all the way from 0 K we could write:
\[ S(T) = S(0) + \int_{0}^{T} C_p dT \nonumber \]
It is tempting to set the \(S(0)\) to zero and make the entropy thus an absolute quantity. As we have seen with enthalpy, it was not really possible set \(H(0)\) to zero. All we did was define \(ΔH\) for a particular process, although if \(C_p\) data are available we could construct an enthalpy function (albeit with a floating zero point) by integration of \(C_P\) (instead of \(C_p/T\)!).
Still for entropy \(S\) the situation is a bit different than for \(H\). Here we can actually put things on an absolute scale. Both Nernst and Planck have proposed to do so. Nernst postulated that for a pure and perfect crystal \(S\) should indeed to go to zero as \(T\) goes to zero. For example, sulfur has two solid crystal structure, rhombic and monoclinic. At 368.5 K, the entropy of the phase transition from rhombic to monoclinic, \(S_{(rh)}\rightarrow S_{(mono)}\), is:
\[\Delta_\text{trs}S(\text{368.5 K})=1.09\;\sf\frac{J\cdot mol}{K} \nonumber \]
As the temperature is lowered to 0 K, the entropy of the phase transition approaches zero:
\[\lim_{T\rightarrow 0}\Delta_rS=0 \nonumber \]
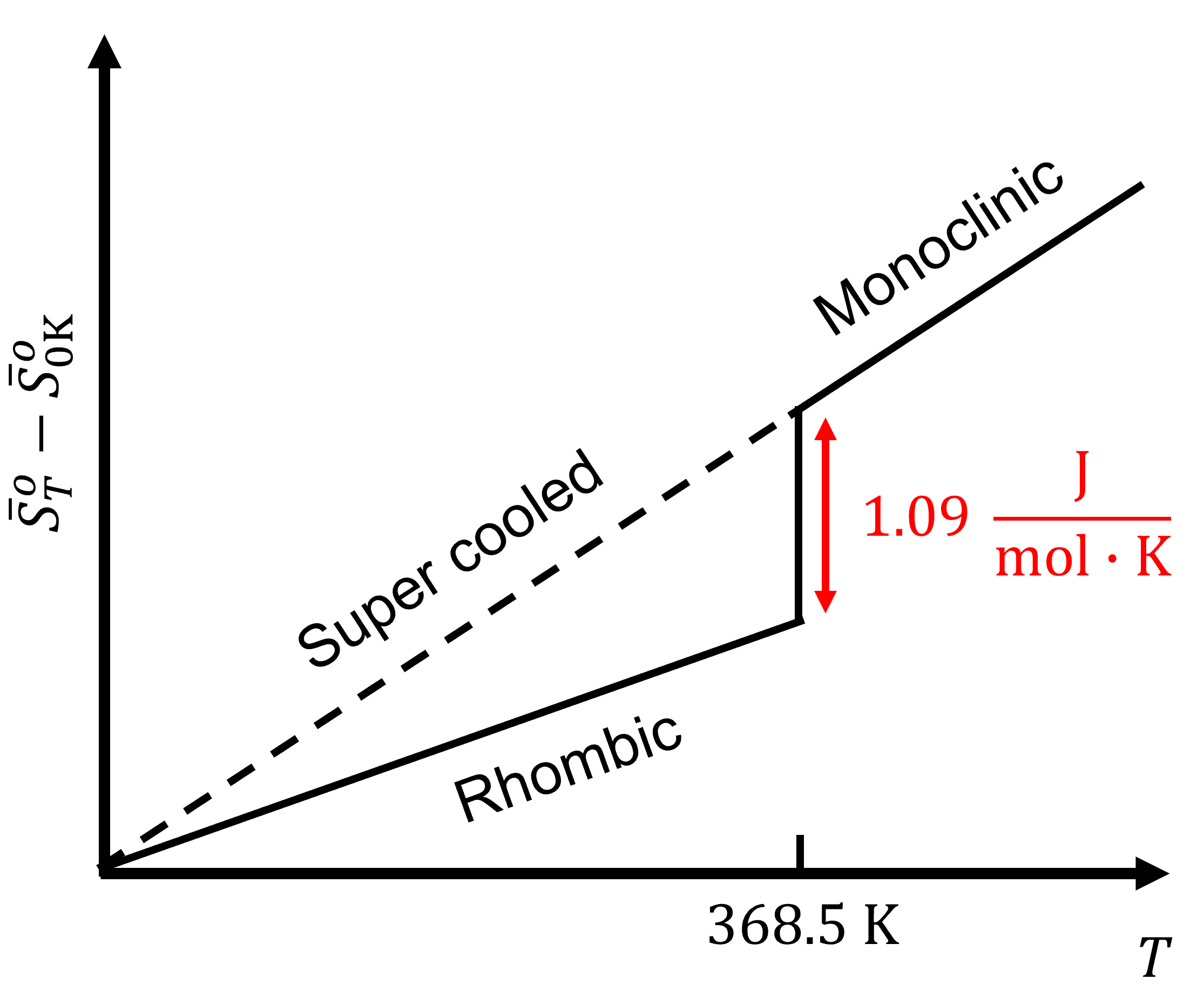
This shows that the entropy of the two crystalline forms are the same. The only way is if all species have the same absolute entropy at 0 K. For energy dispersal at 0 K:
- Energy is as concentrated as it can be.
- Only the very lowest energy states can be occupied.
For a pure, perfect crystalline solid at 0 K, there is only one energetic arrangement to represent its lowest energy state. We can use this to define a natural zero, giving entropy an absolute scale. The third Law of Thermodynamics states that the entropy of a pure substance in a perfect crystalline form is 0 \(\sf\frac{J}{mol\cdot K}\) at 0 K:
\[{\bar{S}}_{0\text{ K}}^\circ=0 \nonumber \]
This is consistent with our molecular formula for entropy:
\[S=k\ln{W} \nonumber \]
For a perfect crystal at 0 K, the number of ways the total energy of a system can be distributed is one (\(W=1\)). The \(\ln{W}\) term goes to zero, resulting in the perfect crystal at 0 K having zero entropy.
It is certainly true that for the great majority of materials we end up with a crystalline material at sufficiently low materials (although there are odd exceptions like liquid helium). However, it should be mentioned that a completely perfect crystal can only be grown at zero Kelvin! It is not possible to grow anything at 0 K however. At any finite temperature the crystal always incorporates defects, more so if grown at higher temperatures. When cooled down very slowly the defects tend to be ejected from the lattice for the crystal to reach a new equilibrium with less defects. This tendency towards less and less disorder upon cooling is what the third law is all about.
However, the ordering process often becomes impossibly slow, certainly when approaching absolute zero. This means that real crystals always have some frozen in imperfections. Thus there is always some residual entropy. Fortunately, the effect is often too small to be measured. This is what allows us to ignore it in many cases (but not all).
We could state the Third law of thermodynamics as follows:
The entropy of a perfect crystal approaches zero when T approaches zero (but perfect crystals do not exist).
Another complication arises when the system undergoes a phase transition, e.g. the melting of ice. As we can write:
\[Δ_{fus}H= q_P \nonumber \]
If ice and water are in equilibrium with each other the process is quite reversible and so we have:
\[Δ_{fus}S = \dfrac{q_{rev}}{T}= \dfrac{Δ_{fus}H}{T} \nonumber \]
This means that at the melting point the curve for \(S\) makes a sudden jump by this amount because all this happens at one an the same temperature. Entropies are typically calculated from calorimetric data (\(C_P\) measurements e.g.) and tabulated in standard molar form. The standard state at any temperature is the hypothetical corresponding ideal gas at one bar for gases.
In table 21.3 a number of such values are shown. There are some clear trends. E.g. when the noble gas gets heavier this induces more entropy. This is a direct consequence of the particle in the box formula: It has mass in the denominator and therefore the energy levels get more crowded together when m increases: more energy levels, more entropy.
The energy levels get more crowded together when \(m\) increases: more energy levels, more entropy
Tabulation of \(H\), \(S\) and \(G\). Frozen entropy
There are tables for \(H^\circ(T)-H^\circ(0)\), \(S^\circ(T)\) and \(G^\circ(T)-H^\circ(0)\) as a function of temperature for numerous substances. As we discussed before the plimsoll defines are standard state in terms of pressure (1 bar) and of concentration reference states, if applicable, but temperature is the one of interest.
For most substances the Third Law assumption that \(\lim{S^\circ(T)}\) for \(T\rightarrow 0 = 0\) is a reasonable one but there are notable exceptions, such as carbon monoxide. In the solid form, carbon monoxide molecules should ideally be fully ordered at absolute zero, but because the sizes of the carbon atoms and the oxygen atoms are very close and the dipole of the molecule is small, it is quite possible to put in a molecule 'upside down', i.e. with the oxygen on a carbon site and vice versa. At higher temperatures, at which the crystal is formed, this lowers the Gibbs energy (\(G\)) because it increases entropy. In fact we could say that if we could put each molecule into the lattice in two different ways, the number of ways \(W_{disorder}\) we can put N molecules in into the lattice is 2N. This leads to an additional contribution to the entropy of
\[S_{disorder} = k\,\ln{W_{disorder}}= N k \ln 2 = R \ln 2 = 5.7\, \frac{\text{J}}{\text{mol}\cdot\text{K}}) \nonumber \]
Although at lower temperatures the entropy term in \(G = H-TS\) becomes less and less significant and the ordering of the crystal to a state of lower entropy should become a spontaneous process, in reality the kinetics are so slow that the ordering process does not happen and solid CO therefore has a non-zero entropy when approaching 0 K.
In principle all crystalline materials have this effect to some extent, but CO is unusual because the concentration of 'wrongly aligned' entities is of the order of 50% rather than say 1 in 1013 (a typical defect concentration in say single crystal silicon).

