19.3: Work and Heat are not State Functions
- Page ID
- 13701
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Heat and work are path functions
Heat (\(q\)) and work (\(w\)) are path functions, not state functions:
- They are path dependent.
- They are energy transfer → they are not intrinsic to the system.
Functions that depend on the path taken, such as work (\(w\)) and heat (\(q\)), are referred to as path functions.
Reversible versus irreversible
Let's consider a piston that is being compressed at constant temperature (isothermal) to half of its initial volume:
- Start with cylinder 1 liter, both external and internal pressure 1 bar.
- Peg the piston in a fixed position.
- Put cylinder in a pressure chamber with \(P_{ext}=2\) bar.
- Suddenly pull the peg.

The piston will shoot down till the internal and external pressures balance out again and the volume is 1/2 L. Notice that the external pressure was maintained constant at 2 bar during the peg-pulling and that the internal and external pressures were not balanced at all time. In a \(P-V\) diagram of an ideal gas, \(P\) is a hyperbolic function of \(V\) under constant temperature (isothermal), but this refers to the internal pressure of the gas. It is the external one that counts when computing work and they are not necessarily the same. As long as \(P_{external}\) is constant, work is represented by a rectangle.
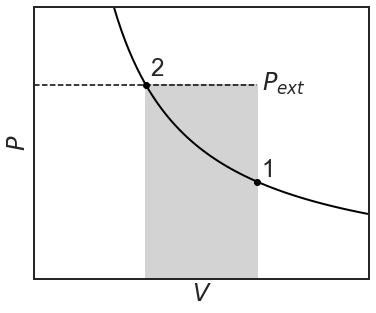
The amount of work being done is equal to the shaded region and in equation:
\[w=-\int^{V_2}_{V_1}{PdV}=-P_{ext}(V_2-V_1)=-P\Delta V \nonumber \]
This represents the maximum amount of work that can be done for an isothermal compression. Work is being done on the system, so the overall work being done is positive. Let's repeat the experiment, but this time the piston will compress reversibly over infinitesimally small steps where the \(P_{ext}=P_{system}\):
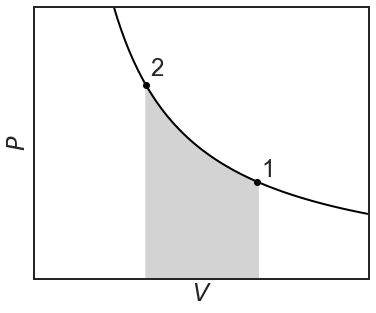
For an ideal gas, the amount of work being done along the reversible compression is:
\[w=-\int^{V_2}_{V_1}{PdV}=-nRT\int^{V_2}_{V_1}{\frac{1}{V}}=-nRT\ln{\left(\frac{V_2}{V_1}\right)} \nonumber \]
The amount of work being done to the two systems are not the same in the two diagrams (see the gray areas). Work is not a state, but a path function, as it depends on the path taken. You may say, what's the big difference. In both cases, the system is compressed from state 1 to state 2. The key is the word suddenly. By pegging the position in place for the first compression, we have created a situation where the external pressure is higher than the internal pressure (\(P_{ext}>P\)). Because work is done suddenly by pulling the peg out, the internal pressure is struggling to catch up with the external one. During the second compression, we have \(P_{ext}=P\) at all times. It's a bit like falling off a cliff versus gently sliding down a hill. Path one is called an irreversible path, the second a reversible path.
A reversible path is a path that follows a series of states at rest (i.e., the forces are allowed to balance at all times). In an irreversible one the forces only balance at the very end of the process.
Notice that less work is being done on the reversible isothermal compression than the one-step irreversible isothermal compression. In fact, the minimum amount of work that can be done during a compression always occurs along the reversible path.
Isothermal Expansion
Let's consider a piston that is being expanded at constant temperature (isothermal) to twice of its initial volume:
- Start with cylinder 1 liter in a pressure chamber with both an external and internal pressure of 2 bar.
- Peg the piston in a fixed position.
- Take the cylinder out of the pressure chamber with Pext= 1 bar.
- Suddenly pull the peg.

The piston will shoot up till the internal and external pressures balance out again and the volume is 2 L. Notice that the external pressure was maintained constant at 1 bar during the peg-pulling and that the internal and external pressures were not balanced at all time.
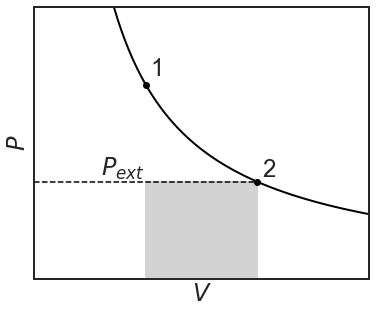
The amount of irreversible work being done is again equal to the shaded region and the equation:
\[w=-P\Delta V=-P_{ext}(V_2-V_1)=-P\Delta V \nonumber \]
This represents the minimum amount of work that can be done for an isothermal expansion. Work is being done on the system, so the overall work being done is negative. Let's repeat the experiment, but this time the piston will compress reversibly over infinitesimally small steps where the \(P_{ext}=P_{system}\):

Notice that not only is more work is being done than the one-step irreversible isothermal expansion, but it is the same amount of work being done as the reversible isothermal compression. This is the maximum amount of work that can be done during an expansion.

