19.2: Pressure-Volume Work
- Page ID
- 13700
Work in general is defined as a product of a force \(\textbf{F}\) and a path element \(\textbf{ds}\). Both are vectors and work is computed by integrating over their inner product:
\[w = \int \textbf{F} \cdot \textbf{ds} \nonumber \]
Moving an object against the force of friction as done in the above dissipation experiment is but one example of work:
\[w_{friction} = \int \textbf{F}_\text{friction} \cdot \textbf{ds} \nonumber \]
We could also think of electrical work. In that case we would be moving a charge e (e.g. the negative charge of an electron) against an electrical (vector) field \(\textbf{E}\). The work would be:
\[w_{electical} = \int e \textbf{E} \cdot \textbf{ds} \nonumber \]
Other examples are the stretching of a rubber band against the elastic force or moving a magnet in a magnetic field etc, etc.
Pressure-volume (\(PV\)) work
In the case of a cylinder with a piston, the pressure of gas molecules on the inside of the cylinder, \(P\), and the gas molecules external to the piston, \(P_\text{ext}\) both exert a force against each other. Pressure, (\P\), is the force, \(F\), being exerted by the particles per area, \(A\):
\[P=\frac{F}{A} \nonumber \]
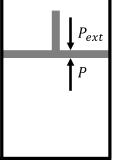
We can assume that all the forces generated by the pressure of the particles operate parallel to the direction of motion of the piston. That is, the force moves the piston up or down as the movement of the piston is constrained to one direction. The piston moves as the molecules of the gas rapidly equilibrate to the applied pressure such that the internal and external pressures are the same. The result of this motion is work:
\[w_{volume} = \int \left( \dfrac{F}{A} \right) (A\,ds) = \int P\,dV \label{Volume work}\]
This particular form of work is called pressure-volume (\(PV\)) work and will play an important role in the development of our theory. Notice however that volume work is only one form of work.
It is important to create a sign convention at this point: positive heat, positive work is always energy you put in into the system. If the system decides to remove energy by giving off heat or work, that gets a minus sign.
In other words: you pay the bill.
To comply with this convention we need to rewrite volume work (Equation \(\ref{Volume work}\)) as
\[w_{PV} = - \int \left( \dfrac{F}{A} \right) (A\,ds) = - \int P\,dV \nonumber \]
Hence, to decrease the volume of the gas (\(\Delta V\) is negative), we must put in (positive) work.
Thermodynamics would not have come very far without cylinders to hold gases, in particular steam. The following figure shows when the external pressure, \(P_\text{ext}\), is greater than and less than the internal pressure, \(P\), of the piston.
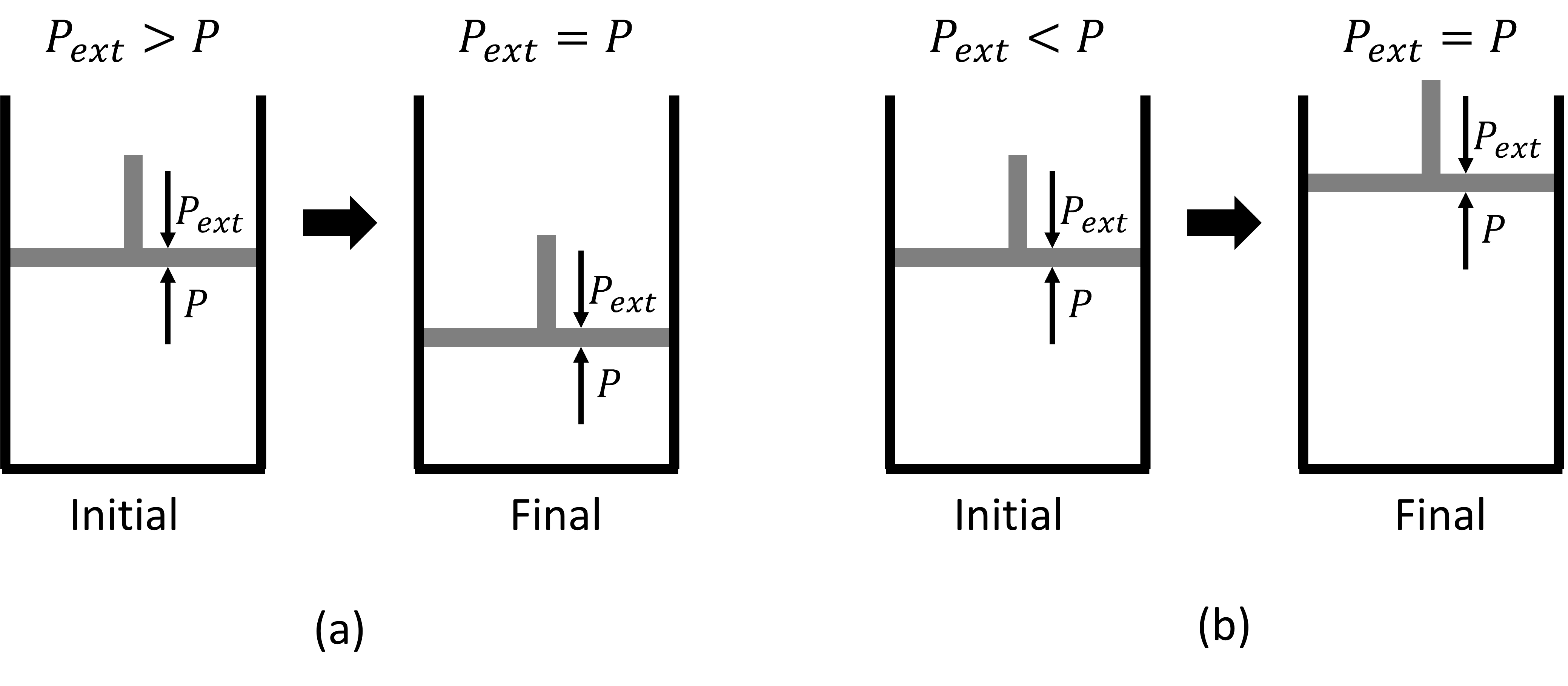
If the pressure, \(P_\text{ext}\), being exerted on the system is constant, then the integral becomes:
\[w = -P_\text{ext}\int_{V_{initial}}^{V_{final}}dV = -P_\text{ext}\Delta V \label{irreversible PV work} \]
Since the system pressure (inside the piston) is not the same as the pressure exerted on the system, the system is not in a state of equilibrium and cannot be shown directly on and \(PV\) diagram. This type of process is called an irreversible process. For a system that undergoes irreversible work at constant external pressure, we can show the amount of work being done on a \(PV\) diagram despite not being able to show the process itself.

Note that the external pressure, \(P_\text{ext}\), exerted on the system is constant. If the external pressure changes during the compression, we must integrate over the whole range:
\[ w = - \int_{V_{initial}}^{V_{final}}P_\text{ext}(V)\, dV \nonumber \]

