16.E: The Properties of Gases (Exercises)
- Page ID
- 13655
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)These are homework exercises to accompany Chapter 16 of McQuarrie and Simon's "Physical Chemistry: A Molecular Approach" Textmap.
Q16.10
One liter of N2 (g) at 2.1 bar and two liters of Ar(g) at 3.4 bar are mixed in a 4.0-L flask to form an ideal-gas mixture. Calculate the value of the final pressure of the mixture if the initial and final temperature of the gases are the same. Then, repeat this calculation if the initial temperatures of the N2 (g) and Ar(g) are 304 K and 402 K, respectively, and the final temperature of the mixture is 377 K. (Assume ideal-gas behavior.)
S16.10
Using the ideal gas law, we can find the number of moles of each gas.
\( n_{N_2} = \dfrac{P_{N_2} V_{N_2}}{RT} = \dfrac{(2.1x10^{5} Pa)*(1x10^{-3} m^3)}{RT} = \dfrac{210 Pa * m^3}{RT} \)
\( n_{Ar} = \dfrac{P_{Ar} V_{Ar}}{RT} = \dfrac{(3.4x10^{5} Pa)*(2x10^{-3} m^3)}{RT} = \dfrac{680 Pa * m^3}{RT} \)
The total moles of gas in the final mixture is the sum of the moles of each gas in the mixture, which is
\( \dfrac{210 Pa * m^3}{RT} + \dfrac{680 Pa * m^3}{RT} = \dfrac{890 Pa * m^3}{RT} \)
Therefore,
\( P = \dfrac{nRT}{V} = \dfrac{890 Pa * m^3}{0.0040 m^3} = 2.2 x 10^5 Pa = 2.2 bar \)
Now, considering the initial temperatures of the gases are different from each other and from the final temperature of the mixture, we calculate the total number of moles to be
\( n_{total} = n_{N_2} + n_{Ar} = \dfrac{210 Pa * m^3}{R*(304 K)} + \dfrac{680 Pa * m^3}{R*(402 K)} \)
Substituting this into the ideal gas law, we get the final pressure to be
\( P= [ \dfrac{210 Pa * m^3}{R*(304 K)} + \dfrac{680 Pa * m^3}{R*(402 K)} ] * \dfrac{R*(377 K)}{0.0040 m^3} = 2.2 x 10^5 Pa = 2.2 bar \)
Q16.12
What is the molar Gas Constant in units of cm3 torr K-1 mol-1.
S16.12
We know \(R=0.082058 L\cdot atm\cdot mol^{-1}K^{-1}\)
using dimensional analysis:
\[R=0.082058 L\cdot atm\cdot mol^{-1}K^{-1}\times \frac{760torr}{1 atm} \times \frac{1 dm^3}{1L} \times \frac{1 dm^3}{1000cm^3}\]
\[R=0.0623639 cm^3\cdot atm\cdot mol^{-1}K^{-1}\]
Q16.13
Use the van der Waals equation to plot the compressibility factor, Z, against P for methane for T = 180 K, 189 K, 190 K, 200 K, and 250 K.
S16.13
First, calculate Z as a function of \(\bar{V}\) and \(P\) as a function of \(\bar{V}\) and plot \(Z\) versus \(P\)
For methane, a = 2.3026 \(dm^{6}\cdot bar\cdot mol^{-2} \) and b = 0.043067 \(dm^{3}\cdot mol^{-1} \)
\[ Z = \dfrac{P\bar{V}}{RT} \]
and the van der Waals equation of state is:
\[ P = \dfrac{RT}{\bar{V} - b} - \dfrac{a}{\bar{V}^2}\]
Then create a parametric plot of Z versus P for the suggested temperatures as shown below.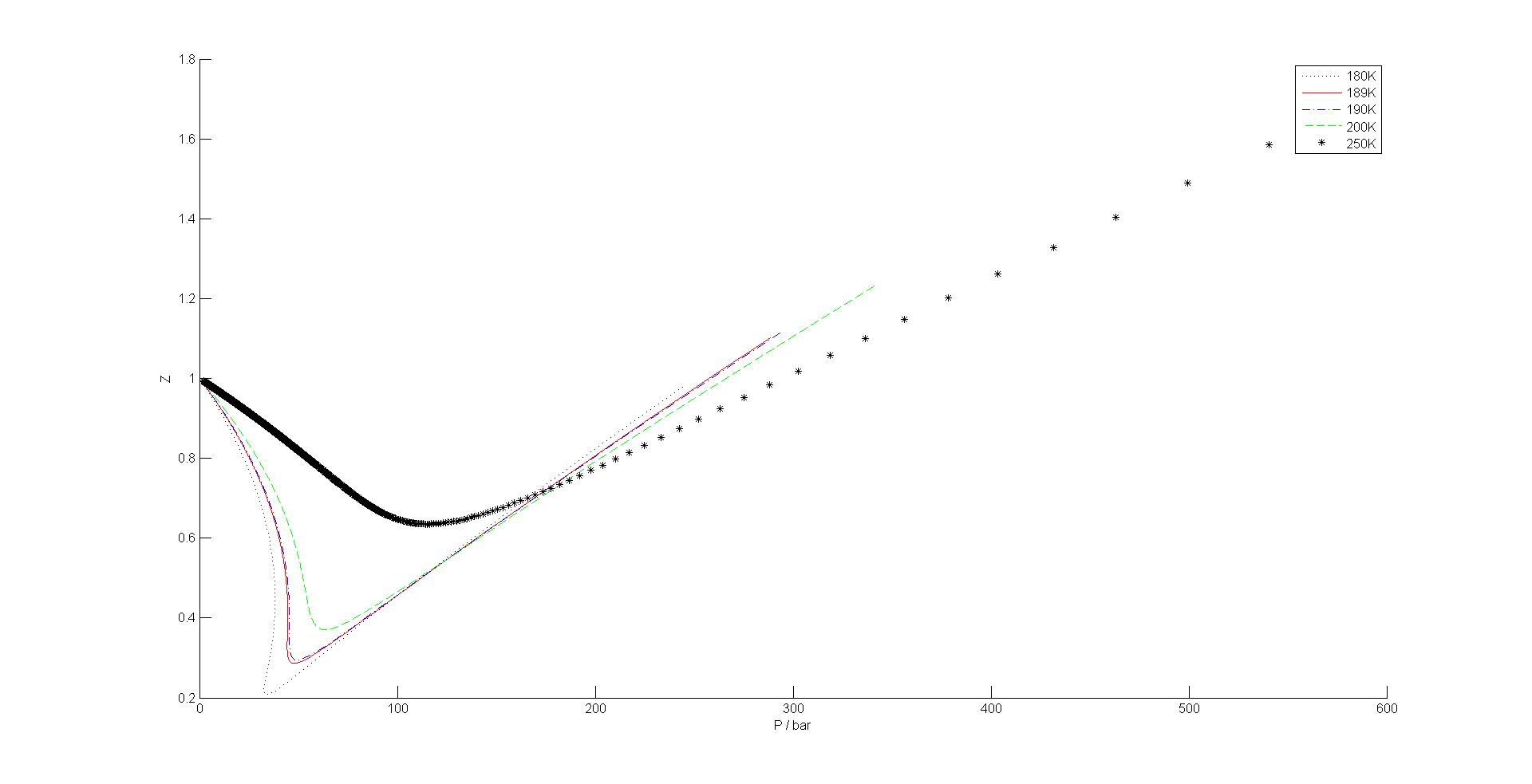
Q16-15
Define the equation that could be solved by using the Netwon-Raphson method to find the molar volume of O2 at 300K and 200atm. Use the van der Waals anf Redlich-Kwong equations.
Constants:
- van der Waals: $$a = 1.3820 dm^{6}*bar*mol,b=0.031860 dm^{3}*mol^{-1}$$
- Redlich-Kwong: $$A = 17.411 dm^{6}*bar*mol^{-2}*K^{1/2},B=0.022082 dm^{3}*mol^{-1}$$
S16.15
Solving van der Waals equation for volume produces:
$$\bar{V}^{3} - (b + \dfrac{RT}{P})\bar{V}^{2} + \dfrac{a}{P}\bar{V} - \dfrac{ab}{P}=0\]
Plugging in constants gives:
$$\bar{V}^{3} - 0.15486\bar{V}^{2} + 0.00691\bar{V} - 0.00022015=0\]
which can be solved numerically to find molar volume.
The Redlich-Kwong equation can be written as a cubic in volume:
$$\bar{V}^{3} - \dfrac{RT}{P}\bar{V}^{2} - \left(B^{2} + \dfrac{BRT}{P} - \dfrac{A}{T^{1/2}P}\right)\bar{V} - \dfrac{AB}{T^{1/2}P} = 0\]
Plugging in constants gives:
$$\bar{V}^{3} - 0.123\bar{V}^{2} + 0.001822\bar{V} - 0.00011099 = 0\]
which can be solved numerically to find molar volume.
Q16.16
Compare the Redlich-Kwong and the van der Waals equations for ethane. Take the molar volume to be 0.09416 .
S16.16
van der Waals:
$$P = \dfrac{RT}{\bar{V}-b}-\dfrac{a}{(\bar{V})^2}\]
Reference Table 16.3 for a, b
$$P = \dfrac{0.083145*400}{.09416-0.065144}-\dfrac{5.5818}{(0.09416)^2}\]
Redlich-Kwong equation of state improved the accuracy of the van der Waals equation by adding a temperature dependence for the attractive term:
$$P = \dfrac{RT}{\bar{V}-B} - \dfrac{A}{T^(\dfrac{1}{2})\bar{V}(\bar{V}+B)}\]
Reference Table 16.4 for A, B
$$P = \dfrac{0.083145*400}{0.09416-0.045153} - \dfrac{98.831}{400^(\dfrac{1}{2})0.09416*(0.09416+0.62723)}\]
Q16.17
\[p=\dfrac{RT}{\dfrac{V}{n}-b}-\dfrac{a}{\sqrt{T}\dfrac{V}{n}\big( \dfrac{V}{n}+b\big) }\]
\[ \big (p+\dfrac{n^{2}a}{V^{2}} \big) (V-nb)=nRT\]Use the equations above to calculate the temperature of a system with \(1.5 \ mol\) of methane at \(300 \ K\) confined to a volume of \(100 \ cm^{3}\). Compare the two calculated pressures.
S16.17
\(R = 82.057338 \dfrac{cm^{2} atm }{K \ mol} \)
Redlich-Kwong constants: \(a = 31.59\times 10^{6} \ (atm)(K^{\frac{1}{2}})\big( \dfrac{cm^{3}}{mol} \big) ^{2} \) and \(b = 29.6 \ \dfrac{cm^{3}}{mol}\)
Van der Waals constants: \(a = 2.25 \times 10^{6} \ (atm) \big( \dfrac{cm^{3}}{mol} \big) ^{2} \) and \(b = 42.8 \ \dfrac{cm^{3}}{mol}\)
Redlich-Kwong equation: \(p=\dfrac{82.057338 \dfrac{cm^{2} atm }{K \ mol} \ 300\ K}{\dfrac{100 \ cm^{3}}{1.5 \ mol}-29.6 \ \dfrac{cm^{3}}{mol}}-\dfrac{31.59 \times 10^{6} \ (atm)(K^{\frac{1}{2}})\big( \dfrac{cm^{3}}{mol} \big) ^{2}}{\sqrt{300 \ K}\dfrac{100 \ cm^{3}}{1.5 \ mol}\big( \dfrac{100 \ cm^{3}}{1.5 \ mol}+29.6 \ \dfrac{cm^{3}}{mol}\big) } = 379.95\ atm\)
Van der Waals equation: \( p =\dfrac{(1.5 \ mol)(82.057338 \dfrac{cm^{2} atm }{K \ mol})(300\ K)}{(100 \ cm^{3})-(1.5\ mol)(42.8 \ \dfrac{cm^{3}}{mol})} -\dfrac{(1.5\ mol)^{2}(2.25 \times 10^{6} \ (atm) \big( \dfrac{cm^{3}}{mol} \big) ^{2} )}{(100 \ cm^{3})^{2}} = 525.2\ atm\)
There is a \(145.25\ atm\) difference in the calculated pressures.
Q16.20
The following equation can be used to relate the pressure of propane to its density at temperatures below 400 K:
\[ P = 33.258\rho - 7.5884\rho^{2} + 1.0306\rho^{3} - 0.058757\rho^{4} - 0.0033566\rho^{5} + 0.00060696\rho^{6} \]
where the pressure (P) is in bar and the density ( \(\rho \)) is in \(\frac{mol}{L} \) and ranges from \( 0 \frac{mol}{L} \leq \rho \leq 12.3 \frac{mol}{L} \).
Calculate and plot the pressure for the given density range using:
- the equation given above
- the Van der Waals equation of state
- the Redlich-Kwong equation of state
Compare your results from the above parts.
S16.20
a.) Straight forward to calculate.
Even though straight forward, should still put solution for students.
graph plotted using matlab.
b.) The following constants were used in the equation below:
\(a = 9.3919 \dfrac{L^{2} bar}{mol^{2}} \) and \(b = 0.09049 \dfrac{L}{mol} \)
\[P_{VDW} = \dfrac{RT}{\overline{V}-b} - \dfrac{a}{\overline{V}^{2}} \]
c.) The following constants were used in the equation below:
\(a = 183.01 \dfrac{L^{2} bar}{mol^{2}} \) and \(b = 0.06272 \dfrac{L}{mol} \)
\[P_{RK} = \dfrac{RT}{\overline{V}-b} - \dfrac{a}{\sqrt{T}\overline{V} (\overline{V}+b)} \]
As can be seen by the plot, the Van der Waals equation of state deviates greatly from the empirical fit at higher densities. The Redlich-Kwong equation provides a reasonable approximation to the empirical data. (All calculations were done in MATLAB, and the above plot was produced by me)
Q16.21
Use the data below to evaluate the van der waals and Redlich Kwong constants for benzene.
| Species | Tc/K | Pc/bar | Pc/atm | Vnc/L mol-1* | PcVnc/RTc |
|---|---|---|---|---|---|
| Benzene | 561.75 | 48.758 | 48.120 | 0.256 | 0.26724 |
*n to indicate molar volume
Van Der Waals
\(a = \dfrac{27(RT_c)^2}{64P_c} \,and \,b = \dfrac{RT_c}{8P_c}\)
Redlich-Kwong
\(A = 0.42748\dfrac{R^2T_c^{\dfrac{5}{2}}}{P_c} \,and \,B = 0.08664\dfrac{RT_c}{P_c}\)
S16.21
Van Der Waals
a = \(\dfrac{27*(0.083145 dm^3 \cdot bar \cdot mol^{-1}K^{-1})^2*(561.75 K)^2}{64*48.758 bar} = {\bf 18.8754 \, dm^6 \cdot atm \cdot mol^{-2}}\)
b = \(\dfrac{(0.083145 dm^3 \cdot bar \cdot mol^{-1}K^{-1})^2*(561.75 K)^2}{8*48.758 bar} = {\bf 5.5927 \, dm^3 \cdot mol^{-1}}\)
Redlich-Kwong
\(A = 0.42748*\dfrac{(0.083145 dm^3 \cdot bar \cdot mol^{-1}K^{-1})^2*(561.75 K)^{\dfrac{5}{2}}}{48.758 bar} = {\bf 453.315 \, dm^6 \cdot atm \cdot mol^{-2}\cdot K^{\dfrac{1}{2}}} \)
\(B = 0.42748*\dfrac{(0.083145 dm^3 \cdot bar \cdot mol^{-1}K^{-1})^2*(561.75 K)^2}{48.758 bar} = {\bf 19.126\, dm^3 \cdot mol^{-1}}\)
Q16.22
Show that the van der Waals equation for argon at T = 142.69 K and P = 35.00 atm can be written as
\[\overline {V}^3 - 0.3664\overline {V}^2+0.001210=0 \]
where, for convenience, we have suppressed the units in the coefficients. Use the Newton-Raphson method (MathChapter G) to find the three roots to this equation, and calculate the values of the density of liquid and vapor in equilibrium with each other under these conditions.
S16.22
Using Table 16.3, we can get the values of a and b for argon to use in Van der Waals equation of state.
By doing this, you can isolate \( \overline {V} \) in van der Waals equation of state. Next, by applying the Newton-Raphson method to the function given by van der Waals equation (which is only dependent on \( \overline {V} \) ), and the derivative of the function, we find the roots to the equation. On the case here, the smallest root represents the molar volume of liquid argon, and the largest root represents the molar volume of vapor argon.
Q16.23
Calculate the Volume occupied by \(50\ kg\) of propane at \(50^{\circ}C\) and \(35\ bar\), using the Redlich-Kwong equation of state and the Peng-Robinson equation of state.
S16.23
Redlich-Kwong equation of state:
\[P = \frac{RT}{v-b} - \frac{a}{v(v+b)}\]
\(v\) is volume of gas per mole.
we have \(T = 50^{\circ} C = 323\ K\) , \(P = 35\ bar = 35 \times (10^5) Pa\)
For propane, we have \(P_{c} =42.4924\ bar = 42.4924 \times 10^5 Pa\) and \(T_{c} = 369.522\ K\)
so we have \(a = \frac{0.42748 R^2 T_{c}^{2.5}}{P_{c}T^{0.5}}\) ;
\(b = \frac{0.08664 * R*T_{c}}{P_{c}}\)
so, \(a = \frac{0.42748 (8.314^2) 369.522^{2.5}}{42.4924 \times 10^5(323^{0.5})} = 1.015603\)
\(b = \frac{(0.08664) (8.314)(369.522)}{42.4924 \times 10^5} = 6.2640829 \times 10^{-5}\)
so, \(P = \frac{RT}{v-b} - \frac{a}{v(v+b)}\)
\((35*(10^5)) = \frac{(8.314)(323)}{ v-(6.2640829 \times 10^{-5})} - \frac{1.015603}{v(v+6.2640829 \times 10^{-5})}\)
The only real solution is
\(v = 0.00010933 \frac{m^3}{mol}\)
so In \(50\ Kg\) propane, number of moles = \(\frac{50*1000}{44.10 } = 1133.78684\)
total volume occupied by \(50\ Kg\) propane at the specified conditions = \((1133.78684)(0.00010933) = 0.1239569 m^3 = 123.9569\) Liters is the answer.
Peng - Robinson's equation of state:
\(P = \frac{RT} {v-b} -\frac{ a}{v(v+b) + b(v-b)}\)
\(a = 0.45724R^2 * T_{c}^2 * \frac{\alpha}{P_c}\)
\(b = 0.0778 R \frac{T_c}{P_c}\)
\(\alpha = 1 + S(1- \sqrt{T_r})\)
\(S = 0.37464 + 1.54226w -0.26992w^2\)
\(T_r = \frac{T}{T_c}\)
we have \(P = 35 \times 10^5 Pa\) and \(T = 323\ K\)
\(P_c =42.4924\ bar = 42.4924 \times 10^5 Pa\) and \(T_c = 369.522\ K\)
we have accentric factor = \(w = 0.152\).
\(T_r = \frac{T}{T_c} = \frac{323}{369.522} = 0.87410\)
\(S = 0.37464 + (1.54226)(0.152) -(0.26992)(0.152^2) =0.602827\)
\(\alpha = 1 + 0.602827*(1- \sqrt{0.87410}) = 1.0392240523\)
\(a = (0.45724)(8.314^2 )( 369.522^2 )\frac{ 1.0392240523}{42.4924 \times 10^5} = 1.055462444\)
\(b = (0.0778 ) (8.314)\frac{369.522} {42.4924 \times 10^5} = 0.0000562494\)
so, by the equation of state:
\((35 \times 10^5) = \frac{(8.314)(323)}{v-0.0000562494} - \frac{1.055462444}{v(v+ 0.0000562494+ 0.0000562494(v- 0.0000562494)}\)
\(v = 0.0000988504 \frac{m^3}{mol}\)
so In \(50\ Kg\) propane, number of moles = \(\frac{(50)(1000)}{44.10} = 1133.78684\)
total volume occupied by \(50\ Kg\) propane at the specified conditions = \((1133.78684)(0.0000988504) = 0.1120752 m^3 = 112.0752\) Liters is the answer.
Q16.25
A way to obtain the expressions for the van der Waals constants is to make \((\frac{\partial P}{\partial\bar{V}})_T\) and \((\frac{\partial^2 P}{\partial\bar{V}^{2}})_T\) zero at the critical point, but why do they equal to zero at critical point? Obtain the equation \(\bar{V_c}\) = \(3b\)from this procedure.
S16.25
\((\frac{\partial P}{\partial\bar{V}})_T\) = 0
\((\frac{\partial^2 P}{\partial\bar{V}^{2}})_T\) = 0
\((\frac{\partial P}{\partial\bar{V}})_T\) = \(\frac{\partial}{\partial\bar{V}}\) \((\frac{RT}{\bar{V}-b} - \frac{a}{\bar{T}^{2}})_T\)
= \(RT\) \((-\frac{1}{(\bar{V}-b)^{2}})\) - \(a\) \((\frac{-2}{\bar{V}^{3}})\)
= \(-\frac{RT}{(\bar{V}-b)^{2}}\) +\(\frac{2a}{\bar{V}^{3}}\)
At critical point,
\(\frac{RT_c}{(\bar{V_c}-b)^2}\) = \(\frac{2a}{\bar{V_c}^{3}}\) by equating \((\frac{\partial P}{\partial\bar{V}})_T\) = 0.
By differentiating the equation \(RT\) \((-\frac{1}{(\bar{V}-b)^{2}})\) - \(a\) \((\frac{-2}{\bar{V}^{3}})\) with respect to \(\bar{V}\),
\((\frac{\partial^{2} P}{\partial\bar{V}^{2}})_T\) = \(\frac{\partial}{\partial \bar{V}}\) \((-\frac{RT}{(\bar{V}-b)^2}\) +\(\frac{2a}{\bar{V}^{3}})_T\)
= \(RT\) \((-\frac{2}{(\bar{V}-b)^{3}})\) + \(2a\) \((\frac{-3}{\bar{V}^{4}})\)
= \(\frac{2RT}{(\bar{V}-b)^{3}}\) - \(\frac{6a}{\bar{V}^{4}}\)
At critical point,
\(\frac{2RT_c}{(\bar{V_c}-b)^{3}}\) = \(\frac{6a}{\bar{V_c}^{4}}\) by equating \((\frac{\partial^2 P}{\partial\bar{V}^{2}})_T\) = 0.
Now,
\(\frac{\frac{2a}{\bar{V_c}^{3}}}{\frac{6a}{\bar{V_c}^{4}}}\) = \(\frac{\frac{RT_c}{(\bar{V_c}-b)^2}}{\frac{2RT_c}{(\bar{V_c}-b)^{3}}}\)
\(\frac{\bar{V_c}}{3}\) = \(\frac{(\bar{V_c}-b)}{2}\)
\(\bar{V_c}\) = \(3b\)
Q16.26
Show that the Redlich-Kwong equation can be rewritten in the following form:
\[\bar(V)^3 - \frac{RT}{P}\bar{V}^2 - (B^2 + \frac{BRT}{P} - \frac{A}{PT^{1/2}})\bar{V} - \frac{AB}{PT^{1/2}} = 0 \]
S16.26
Starting with the Redlich-Kwong equation and manipulating it we get the following:
\[P = \frac{RT}{\bar{V}-B} - \frac{A}{T^{1/2}\bar{V}(\bar{V} + B)}\]
\[ P(\bar{V}-B)T^{1/2}\bar{V}(\bar{V} + B) = RT^{3/2}\bar{V}(\bar{V} + B) - A(\bar{V}-B)\]
\[ PT^{1/2}\bar{V}(\bar{V}^2 - B^2) = RT^{3/2}\bar{V}^2 + RT^{3/2}\bar{V}B - A\bar{V} + AB\]
\[\bar(V)^3 - \frac{RT}{P}\bar{V}^2 - (B^2 + \frac{BRT}{P} - \frac{A}{PT^{1/2}})\bar{V} - \frac{AB}{PT^{1/2}} = 0 \]
Q16.27
Use the results of the previous question, Q16.26, to derive Equations 16.14.
\((a) \bar{V}_{c} = 3.8473B \), \((b) P_{c} = .029894\dfrac{A^{2/3}R^{1/3}}{B^{5/3}}\), and \((c) T_{c} = .34504\left(\frac{A}{BR}\right) ^{2/3}\)
The following are solved from Q16.26 and are necessary to solve for Equation 16.14:
\[1) B = .25992\bar{V}_{c} \] \[2) A = 0.42748\dfrac{R^{2}T^{5/2}_{c}}{P_{c}}\] \[3) \dfrac{P_{c}\bar{V_{C}}}{RT_{c}} = \frac{1}{3} \]
S16.27
From equation (1) we see that solving for \(\bar{V}_{c}\) yields the first equation \[\bar{V}_{c} = 3.8473B \].
From equation (2) we can rewrite the expression with some manipulation as \[ A = .42748RT^{3/2}_{c}\left(\frac{RT_{c}}{P_{c}\bar{V}_{c}}\right)\bar{V}_{c} \]
Substituting equation (3) and 16.14a into the previous equation gives the expression \[A = 3(.42748)RT^{3/2}_{c}(3.8473B) \]
Lastly, solving for \(T_{c}\) gives the equation for 16.14c \[T_{c} = .34504\left(\frac{A}{BR}\right) ^{2/3}\]
Finally, solving for equation 16.14b we must substitute the previously solved 16.14c into equation (2),solving for \(P_{c}\)
\[P_{c} = 0.42748\dfrac{R^{2}T^{5/2}_{c}}{A} = \left(\frac{.42748}{A}\right)R^{2}\left[.34504\left(\frac{A}{BR}\right)^{2/3}\right]^{5/2} = .029894\dfrac{A^{2/3}R^{1/3}}{B^{5/3}}\]
which is equation 16.14b.
Q16.28
Derive the Van der Waals cubic equation of state from
\[\big( P+\frac{a}{\bar{V}^2}\big)\big(\bar{V}-b\big)=RT\]
S16.28
The Van der Waal equation can be rewritten in terms of \(Z\):
\[Z=\frac{P\bar{V}}{RT}=\frac{\bar{V}}{\bar{V}-b}-\frac{a}{RT\bar{V}}\]
solving for \(\bar{V}\)
\[\bar{V}^3-\big(b+\frac{RT}{P}\big)\bar{V}^2 + \frac{a}{P}\bar{V}-\frac{ab}{P}=0\]

