12.2: Symmetry Elements and Operations Define the Point Groups
- Page ID
- 13485
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Symmetry Elements
A symmetry operation is an action that leaves an object looking the same after it has been carried out. For example, if we take a molecule of water and rotate it by 180° about an axis passing through the central O atom (between the two H atoms) it will look the same as before. Each symmetry operation has a corresponding symmetry element, which is the axis, plane (2-dimensional), line (1-dimensional) or point (0-dimensional) with respect to which the symmetry operation is carried out:

The symmetry element consists of all the points that stay in the same place when the symmetry operation is performed. In a rotation, the line of points that stay in the same place constitute a symmetry axis; in a reflection the points that remain unchanged make up a plane of symmetry. The symmetry of a molecule or ion can be described in terms of the complete collection of symmetry operations it possesses. The symmetry elements that a molecule (and any other 3-D object) may possess are discussed below.
Symmetry Operations
The symmetry of a molecule or ion can be described in terms of the complete collection of symmetry operations it possesses. There are five types of operations:
- Identity, \(E\)
- Rotation, \(C_n\)
- Reflection, \(\sigma\)
- Inversion, \(i\)
- Improper Rotation, \(S_n\)
Symmetry Operations
A symmetry operation is a permutation of atoms such that the molecule is transformed into a state indistinguishable from the starting state.
Identity Symmetry, \(E\)
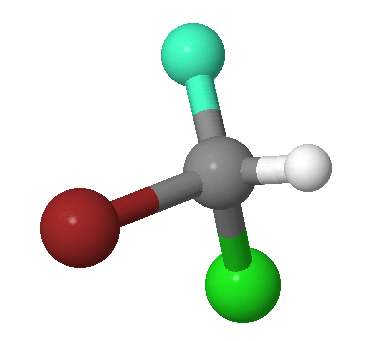
The identity operator, \(E\), consists of doing nothing, and the corresponding symmetry element is the entire molecule. Every molecule possesses at least this operation. For example, the \(\ce{CHFClBr}\) molecule in Figure 12.2.1 . The identify symmetry operation is not indicated since all molecule exhibit this symmetry.
\(n\)-fold Axis of Rotation, \(C_n\)
The rotation operation (sometimes called proper rotation), \(C_n\), rotates an object about an axis by \(2\pi/n\) radians or \(360^{\circ}/n\). Rotation by \(C_n\) leaves the molecule unchanged. The \(H_2O\) molecule has a \(C_2\) axis (Figure 12.2.2 ). Molecules can have more than one \(C_n\) axis, in which case the one with the highest value of \(n\) is called the principal axis. In some high symmetry systems, there may be more than one principal axis. Note that by convention, rotations are counterclockwise about the axis. \(C_n\) rotations are indicated via vectors with labels as indicated below.
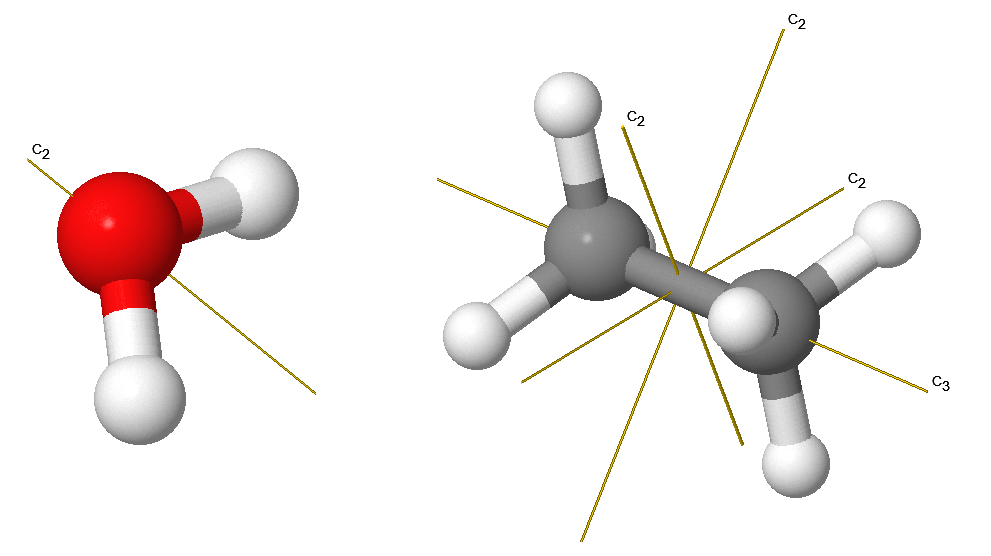
We always want to express rotations in their simplest equivalent fractions of \(m/n\):
\[ C_4^2=C_2 \]
\[ C_6^4=C_3^2 \]
\[ C_8^6=C_4^3 \]
Rotating an object \(n\) times brings the object back to the original object and is equivalent to the identity operation, \(E\):
\[ C_n^n = E \nonumber \]
Linear molecules have a very high rotational symmetry: \(C_\infty\). Examples include diatomics such as \(\text{CO}\), \(\text{NO}\), and \(\text{CO}_2\).
Reflection, \(\sigma\)
Reflection, \(\sigma\), defines the bilateral symmetry about a plane (mirror plane / reflection plane). Reflection in the plane leaves the molecule looking the same. In a molecule that also has an axis of symmetry, a mirror plane that includes the axis is called a vertical mirror plane and is labeled \(\sigma_v\), while one perpendicular to the axis is called a horizontal mirror plane and is labeled \(\sigma_h\). A vertical mirror plane that bisects the angle between two \(C_2\) axes is called a dihedral mirror plane, \(\sigma_d\). If no principal axis exist, \(\sigma_h\) is defined as the plane of the molecule. \(\sigma\) symmetry is indicated as a plane on molecules; since they often bisect atoms, which should be clearly indicated.
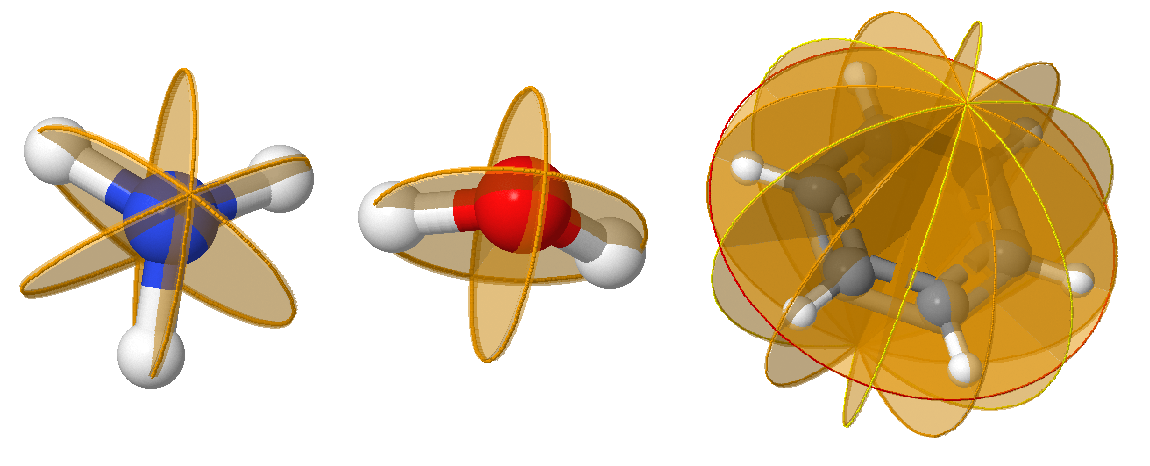
For any mirror plane, performing two successive reflections about the same plane brings objects back to their original configuration:
\[ \sigma\sigma=\sigma^2=E \nonumber \]
Inversion, \(i\)
Inversion, \(i\), through the center of symmetry leaves the molecule unchanged. Inversion consists of passing each point through the center of inversion and out to the same distance on the other side of the molecule. If inversion symmetry exists, a line drawn from any atom through the center will connect with an equivalent atom at an equivalent distance from the center. Examples of molecules with centers of inversion is shown in Figure 12.2.4 . Centers of inversion are indicated via a point, which may or may not overlap with an atoms. The inversion center is always located at the central point of the molecule and there can only be one inversion center in any system. The centers of inversion in the examples below do not overlap with atoms.
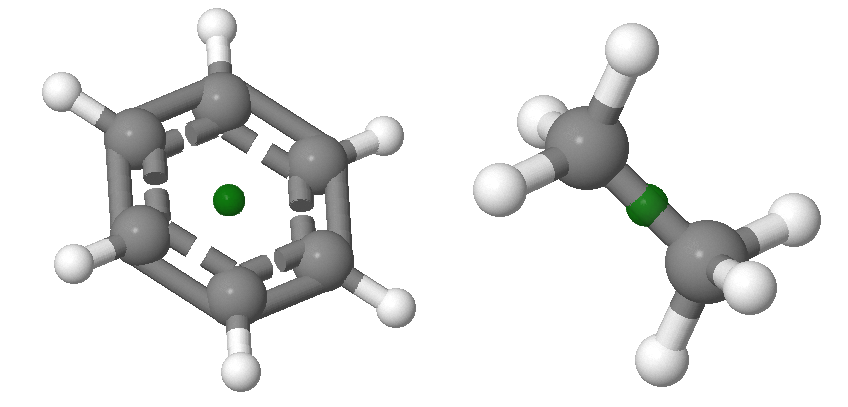
Performing inversion twice in succession brings every point back to its original position:
\[ ii=i^2=E \nonumber \]
Molecules with no inversion symmetry are said to be centrosymmetric.
\(n\)-fold Axis of Improper Rotation, \(S_n\)
Improper rotations, \(S_n\), are also called rotation-reflections. The rotation-reflection operation consists of rotating by \(C_n\) about an axis, followed by reflecting in a plane perpendicular to the same axis. Improper rotation symmetry is indicated with both an axis and a plan as demonstrated in the examples in Figure 12.2.5 .
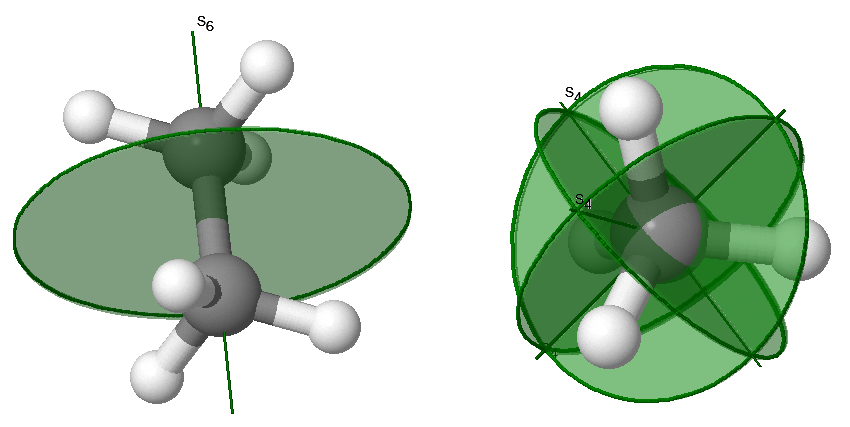
\(S_1\) is the same as reflection and \(S_2\) is the same as inversion.
The lowest-order improper rotation that is not a simpler operation is \(S_3\). The pattern of successive operations depends on if \(n\) is even or odd. The general relationships for \(S_n\) operations are:
- If \(n\) is even, \(S_n^n=E\)
- Molecule returns to original orientation configuration after each full rotation
- There are an even number of rotation operators and reflection operators
- If \(n\) is odd, \(S_n^n=\sigma\) and \(S_n^{2n}=E\)
- First full rotation:
- Molecular does not return to original configuration after first rotation
- There are an odd number of rotation operators and reflection operators
- Second full rotation:
- Molecule returns to original orientation configuration
- There are an even number of rotation operators and reflection operators
- First full rotation:
- When \(m\) is even, there is always a corresponding proper rotation (\(C_n\)):
- \(S_n^m=C_n^m\) when \(m<n\)
- \(S_n^m=C_n^{m-n}\) when \(m>n\) (2nd rotation)
- If \(S_n\) with even \(n\) exists, \(C_{n/2}\) exists
- If \(S_n\) with odd \(n\) exists, then both \(C_n\) and \(\sigma\) perpendicular to \(C_n\) exist
Summary of Symmetry Operations
The identity \(E\) and rotations \(C_n\) are symmetry operations that could actually be carried out on a molecule. For this reason they are called proper symmetry operations. Reflections, inversions and improper rotations can only be imagined (it is not actually possible to turn a molecule into its mirror image or to invert it without some fairly drastic rearrangement of chemical bonds) and as such, are termed improper symmetry operations. These five symmetry operations are tabulated in Table 12.2.1 .
| Symbol Elements | Description | Symbol Operator | Symbol |
|---|---|---|---|
| \(E\) | identity | \(\hat{E}\) | no change |
| \(C_n\) | \(n\)-fold axis of rotation | \(\hat{C}_n\) | Rotation by \(360°/n\) leaves the molecule unchanged |
| \(\sigma\) | plane of symmetry | \(\hat{\sigma}\) | Reflection in the plane leaves the molecule unchanged |
| \(i\) | center of symmetry. | \(\hat{i}\) | Inversion through the center of symmetry leaves the molecule unchanged. |
| \(S_n\) | \(n\)-fold improper rotation | \(\hat{S}_n\) | The rotary reflection operation consists of rotating through an angle \(360°/n\) about the axis, followed by reflecting in a plane perpendicular to the axis. |
Defining the Coordinate System
Conventionally, when imposing a set of Cartesian axes on a molecule (as we will need to do later on in the course), the \(z\) axis lies along the principal axis of the molecule, the \(x\) axis lies in the plane of the molecule (or in a plane containing the largest number of atoms if the molecule is non-planar), and the \(y\) axis makes up a right handed axis system.
Generally, the following conventions are observed to define the coordinate system:
- The origin of the coordinate system is located at the central atom or the center of the molecule.
- The \(z\)-axis is collinear with the highest-order rotational axis (principal axis).
- For planar molecules, if the z-axis is perpendicular to the molecular plane:
- The \(x\)-axis lies in the plane of the molecule and passes through the greatest number of atoms.
- The \(x\)-axis stands perpendicular to the plane
- For non-planar molecules, once the z-axis has been defined, the x-axis is the usually chosen so that the xz plane contains as many atoms as possible.
Molecular Point Groups
It is only possible for certain combinations of symmetry elements to be present in a molecule (or any other object). As a result, we may group together molecules that possess the same symmetry elements and classify molecules according to their symmetry. These groups of symmetry elements are called point groups (due to the fact that there is at least one point in space that remains unchanged no matter which symmetry operation from the group is applied). There are two systems of notation for labeling symmetry groups, called the Schönflies and Hermann-Mauguin (or International) systems. Schönflies notation is used by chemists and spectroscopists, while Crystallographers prefer Hermann-Mauguin notation.The symmetry of individual molecules is usually described using the Schönflies notation, which is used below. The common point groups can be categorized into the following:
- Nonrotational groups
- Single-axis rotationa groups
- Dihedral groups
- Cubic groups
Some of the point groups share their names with symmetry operations, so be careful you do not mix up the two. It is usually clear from the context which one is being referred to.
Nonrotational groups
Nonrotational groups represent the lowest symmetry groups. They include:
\(C_1\) - Contains only the identity (a \(C_1\) rotation is a rotation by 360° and is the same as the identity operation, \(E\)). Molecules that belongs to the \(C_1\) group have no symmetry and are therefore asymmetric.
- Example: CHDFCl
\(C_i\) - Contains the identity \(E\) and a center of inversion \(i\).
- Example: C2H2F2Cl2
\(C_S\) - Contains the identity \(E\) and a plane of reflection \(\sigma\).
Single-axis rotation groups
Single-axis rotation groups are examples of cyclic groups. In cyclic groups, all of the operators commute (Abelian). In their multiplication tables, elements appear along right-to-left diagonals. Knowing this pattern makes it easy to construct multiplication tables! Single-axis rotational groups include:
\(C_n\) - Contains the identity and an \(n\)-fold axis of rotation.
\(C_{nv}\) - Contains the identity, an \(n\)-fold axis of rotation, and \(n\) vertical mirror planes \(\sigma_v\).

\(C_{nh}\) - Contains the identity, an \(n\)-fold axis of rotation, and a horizontal reflection plane \(\sigma_h\) (note that in \(C_{2h}\) this combination of symmetry elements automatically implies a center of inversion).
\(S_n\) - Contains the identity and one \(S_n\) axis. Note that molecules only belong to \(S_n\) if they have not already been classified in terms of one of the preceding point groups (e.g. \(S_2\) is the same as \(C_i\), and a molecule with this symmetry would already have been classified).
Dihedral groups
The dihedral groups have \(n\) two-fold axes perpendicular to the principal \(n\)-fold axis. These \(C_2\) axis are called dihedral axes. Dihedral groups groups include:
\(D_n\) - Contains the identity, an \(n\)-fold axis of rotation, and \(n\) 2-fold rotations about axes perpendicular to the principal axis.
\(D_{nd}\) - Contains the same symmetry elements as \(D_n\) with the addition of \(n\) dihedral mirror planes.
\(D_{nh}\) - Contains the same symmetry elements as \(D_n\) with the addition of a horizontal mirror plane.
- There are \(n\)-fold vertical mirror places (\(\sigma_v\))
- Includes \(n\)-fold improper axis when \(n>2\)
- They are centrosymmetric when \(n\) is even
\(D_{\infty h}\) - Same as \(D_{nh}\), except the principal rotational axis is an infinite-fold \(C_\infty\).
- This is the point group for all linear centrosymmetric linear molecules (e.g. H2, CO2)

Cubic groups
The following groups are the cubic groups, which contain more than one principal axis. The cubic groups are associated with polyhedra that are geometrically related to the cube. All are characterized by the presence of multiple, intersecting, high-order rotational axes. They separate into the tetrahedral groups (\(T_d\), \(T_h\) and \(T\)) and the octahedral groups (\(O\) and \(O_h\)).
\(T_d\) - Contains all the symmetry elements of a regular tetrahedron, including the identity, 4 \(C_3\) axes, 3 \(C_2\) axes, 6 dihedral mirror planes, and 3 \(S_4\) axes e.g. \(\ce{CH_4}\).
- Example: Methane, \(\ce{C_4}\)
\(T\) - Same as for \(T_d\) but no planes of reflection.
\(T_h\) - Same as for \(T\) but contains a center of inversion.
\(O_h\) - The group of the regular octahedron.
- Example: Sulfur hexafluoride, \(\ce{SF_6}\)
\(O\) - Same as for \(O_h\), but with no planes of reflection.
\(I_h\) - Icoshedral, a geometric shape with 20 faces.
- Example: Buckminsterfullerene, (\(\ce{C_{60}}\))
Summary of groups
The final group is the full rotation group \(R_3\), which consists of an infinite number of \(C_n\) axes with all possible values of \(n\) and describes the symmetry of a sphere. Atoms (but no molecules) belong to \(R_3\), and the group has important applications in atomic quantum mechanics. However, we won’t be treating it any further here.
| Nonaxial groups | C1 | Cs | Ci | - | - | - | - | - | - |
|---|---|---|---|---|---|---|---|---|---|
| Cn groups | C2 | C3 | C4 | C5 | C6 | C7 | C8 | - | - |
| Dn groups | D2 | D3 | D4 | D5 | D6 | D7 | D8 | - | - |
| Cnv groups | C2v | C3v | C4v | C5v | C6v | C7v | C8v | - | - |
| Cnh groups | C2h | C3h | C4h | C5h | C6h | - | - | - | - |
| Dnh groups | D2h | D3h | D4h | D5h | D6h | D7h | D8h | - | - |
| Dnd groups | D2d | D3d | D4d | D5d | D6d | D7d | D8d | - | - |
| Sn groups | S2 | - | S4 | - | S6 | S8 | S10 | S12 | |
| Cubic groups | T | Th | Td | O | Oh | I | Ih | - | - |
| Linear groups | C∞v | D∞h | - | - | - | - | - | - | - |
Once you become more familiar with the symmetry elements and point groups described above, you will find it quite straightforward to classify a molecule in terms of its point group. In the meantime, the flowchart shown below provides a step-by-step approach to the problem.
1Though the Hermann-Mauguin system can be used to label point groups, it is usually used in the discussion of crystal symmetry. In crystals, in addition to the symmetry elements described above, translational symmetry elements are very important. Translational symmetry operations leave no point unchanged, with the consequence that crystal symmetry is described in terms of space groups rather than point groups.
Symmetry and Physical Properties
Carrying out a symmetry operation on a molecule must not change any of its physical properties. It turns out that this has some interesting consequences, allowing us to predict whether or not a molecule may be chiral or polar on the basis of its point group.
For a molecule to have a permanent dipole moment, it must have an asymmetric charge distribution. The point group of the molecule not only determines whether the molecule may have a dipole moment, but also in which direction(s) it may point. If a molecule has a \(C_n\) axis with \(n > 1\), it cannot have a dipole moment perpendicular to the axis of rotation (for example, a \(C_2\) rotation would interchange the ends of such a dipole moment and reverse the polarity, which is not allowed – rotations with higher values of \(n\) would also change the direction in which the dipole points). Any dipole must lie parallel to a \(C_n\) axis.
Also, if the point group of the molecule contains any symmetry operation that would interchange the two ends of the molecule, such as a \(\sigma_h\) mirror plane or a \(C_2\) rotation perpendicular to the principal axis, then there cannot be a dipole moment along the axis. The only groups compatible with a dipole moment are \(C_n\), \(C_{nv}\) and \(C_s\). In molecules belonging to \(C_n\) or \(C_{nv}\) the dipole must lie along the axis of rotation.
One example of symmetry in chemistry that you will already have come across is found in the isomeric pairs of molecules called enantiomers. Enantiomers are non-superimposable mirror images of each other, and one consequence of this symmetrical relationship is that they rotate the plane of polarized light passing through them in opposite directions. Such molecules are said to be chiral,2 meaning that they cannot be superimposed on their mirror image. Formally, the symmetry element that precludes a molecule from being chiral is a rotation-reflection axis \(S_n\). Such an axis is often implied by other symmetry elements present in a group.
For example, a point group that has \(C_n\) and \(\sigma_h\) as elements will also have \(S_n\). Similarly, a center of inversion is equivalent to \(S_2\). As a rule of thumb, a molecule definitely cannot have be chiral if it has a center of inversion or a mirror plane of any type (\(\sigma_h\), \(\sigma_v\) or \(\sigma_d\)), but if these symmetry elements are absent the molecule should be checked carefully for an \(S_n\) axis before it is assumed to be chiral.
The word chiral has its origins in the Greek word for hand (\(\chi\)\(\epsilon\)\(\rho\)\(\iota\), pronounced ‘cheri’ with a soft ch as in ‘loch’). A pair of hands is also a pair of non-superimposable mirror images, and you will often hear chirality referred to as ‘handedness’ for this reason.
Summary
All molecules can be described in terms of their symmetry or lack thereof, which may contain symmetry elements (point, line, plane). Identity, rotation, reflection, and inversion are symmetry operations (movement of the molecules such that after the movement, all the atoms of the molecules is coincidental with equivalent atom of the molecule in original).


