5.2: Second Order Ordinary Differential Equations - Oscillations
- Page ID
- 106828
This section is also available in video format: http://tinyurl.com/kq7mrcq
The motion of a frictionless pendulum
We will now use what we learned so far to solve a problem of relevance in the physical sciences. We’ll start with the problem of the pendulum, and as we already discussed in Section 3.2, even if the pendulum is not particularly interesting as an application in chemistry, the topic of oscillations is of great interest due to the fact that atoms in molecules vibrate around their bonds.
The problem of the pendulum was introduced in Figure 3.5, which is reprinted again below:
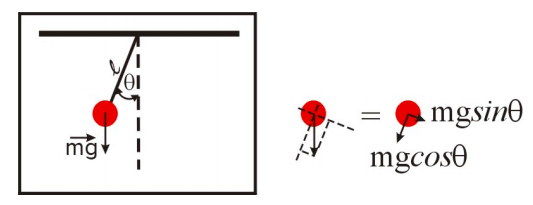
If you took a university physics course, you may recognize that Newton’s second law yields:
\[ \label{eqn2} ml\frac{d^2\theta}{dt^2}+mg\sin{\theta}=0\]
This, unfortunately, is a non-linear differential equation (the dependent variable, \(\theta\), appears as the argument of a transcendental function). As we discussed in Section 3.2, this ODE has no analytical solution. It is possible to solve this equation numerically (and you will do it in the lab), but we cannot get an equation that is the solution of this ODE. We also discussed that we can obtain analytical solutions if we assume that the angle \(\theta\) is small at all times. This means that the solution we get is valid only if the pendulum oscillates very close to the line normal to the ceiling. You may be thinking that studying such a system is boring and useless, but again, as we discussed in Section 3.2, for most molecules at moderate temperatures the displacement of the atoms around their equilibrium position is very small. That is why studying oscillations of systems close to equilibrium makes sense for a chemist.
We already discussed that if \(\theta<<1\), then \(\sin{\theta}\approx\theta\) (see Figure 3.4). Equation \ref{eqn2} can then be simplified to:
\[ \frac{d^2\theta}{dt^2}+\frac{g}{l}\theta=0\]
This equation is linear in \(\theta\), is homogeneous, and has constant coefficients (\(g\) is the acceleration of gravity and \(l\) the length of the rod). The auxiliary equation of this ODE is:
\[\alpha^2+\frac{g}{l}=0 \nonumber\]
and therefore,
\[\alpha=\pm i \sqrt{\frac{g}{l}} \nonumber\]
The general solution is
\[\theta(t)=c_1 e^{\alpha_1t}+c_2 e^{\alpha_2t} \nonumber\]
\[\theta(t)=c_1 e^{i(g/l)^{1/2}t}+c_2 e^{-i(g/l)^{1/2}t} \nonumber\]
We will get the values of the arbitrary constants from the initial conditions. Let’s assume that at time zero the value of \(\theta\) was \(\theta_0<<1\), and the value of \(d\theta/dt\), which is a measure of the velocity, was \(\theta'(0)=0\). Physically, it means that at time zero we are holding the pendulum still. At this point we can either use Euler relationships to simplify our result into a cosine and a sine, or use the initial conditions and use Euler’s relationship later. Either way will work, and how you choose to proceed is a matter of personal taste. Let’s apply the initial conditions now:
\[\theta(t)=c_1 e^{i(g/l)^{1/2}t}+c_2 e^{-i(g/l)^{1/2}t}\rightarrow\theta(0)=c_1+c_2=\theta_0 \nonumber\]
\[\theta'(t)=c_1i(g/l)^{1/2} e^{i(g/l)^{1/2}t}-c_2i(g/l)^{1/2} e^{-i(g/l)^{1/2}t} \nonumber\]
\[\theta'(0)=c_1i(g/l)^{1/2}-c_2i(g/l)^{1/2}=0\rightarrow c_1=c_2 \nonumber\]
Therefore, \(c_1=c_2=\theta_0/2\), and our particular solution is:
\[\theta(t)=\frac{\theta_0}{2}\left(e^{i(g/l)^{1/2}t}+e^{-i(g/l)^{1/2}t}\right) \nonumber\]
From Euler’s relationship we know that \(e^{ix}+e^{-ix}=2cos{x}\), so
\[ \label{eqn3} \theta(t)=\theta_0\cos{\left(\left(\frac{g}{l}\right) ^{1/2}t\right)}\]
This is of course the familiar periodic function that you saw in your physics course. Remember that we got here by assuming \(\theta<<1\) at all times.
As we saw in Section 1.4, the period of the function \(\cos(nx)\) is \(2\pi/n\). The period of the function \(\theta_0\cos{\left(\left(\frac{g}{l}\right) ^{1/2}t\right)}\) is therefore \(P=2\pi \left(\frac{l}{g} \right)^{1/2}\). The period has units of time, and it tells us the time that it takes for the pendulum to complete a whole cycle (see Figure \(\PageIndex{2}\)).
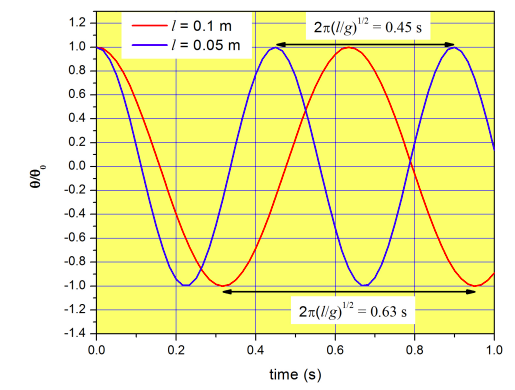
We can also calculate the frequency of the motion, which is just the reciprocal of the period. If the period is the amount of time you need to wait to complete a full cycle, the reciprocal is the number of cycles per unit time. For example, if it takes a pendulum with \(l=0.1 m\) 0.63 seconds to complete a cycle, this means that we get 1.58 cycles per second. The frequency has units of reciprocal time.
The fact that pendula with different lengths have different periods was used by a very creative mind to produce the beautiful display showcased a the lobby of the PSF building at ASU (right across the elevators). There are some videos on YouTube demonstrating the idea (search for pendulum waves), but the one in the physics department at ASU is much more impressive, so go and check it out if you haven’t done so yet.
The pendulum in a viscous medium
The problem we just saw assumed that there was no friction, so the pendulum will oscillate forever without changing the amplitude. Let’s make the problem more realistic from the physical point of view and add a term that accounts for frictional resistance. The force due to friction is usually proportional to the velocity, so this new force introduces a term that depends on the first derivative of \(\theta\):
\[ \frac{d^2\theta}{dt^2}+\gamma \frac{d\theta}{dt}+\frac{g}{l}\theta=0\]
The constant \(\gamma\) depends on the medium, and it will be larger in e.g. water (more friction) than in air (less friction). The auxiliary equation is now
\[\alpha^2+\gamma \alpha+\frac{g}{l}=0 \nonumber\]
and the two roots are:
\[\alpha_{1,2}=\frac{-\gamma \pm\sqrt{\gamma^2-4g/l}}{2} \nonumber\]
and we see that the result will depend on the relative values of \(\gamma^2\) and \(4g/l\). We will analyze the case \(\gamma^2<4g/l\) first (low friction regime). It is useful to always think about what one expects before doing any math. Think about the pendulum without friction, and imagine you do the same experiment in air (small friction). How do you think the plot of \(\theta(t)\) vs \(t\) would look like?
Coming back to the math, let’s call \(a=\sqrt{4g/l-\gamma^2}\) to simplify notation. In the low friction case, \(a\) will be a real number. The two roots will therefore be:
\[\alpha_{1,2}=\frac{-\gamma \pm ia}{2} \nonumber\]
and the general solution will be
\[\theta(t)=c_1 e^{\alpha_1 t}+c_1 e^{\alpha_2 t} \nonumber\]
\[\theta(t)=c_1 e^{-\gamma t/2}e^{ia t/2}+c_2 e^{-\gamma t/2}e^{-ia t/2} \nonumber\]
\[\theta(t)=e^{-\gamma t/2}\left(c_1 e^{ia t/2}+c_2 e^{-ia t/2}\right) \nonumber\]
At this point we can either use the initial conditions and use Euler’s relationship later, or we can use Euler’s equations now and the initial conditions later. Either way should work.
\[\theta(t)=e^{-\gamma t/2}\left[\left(c_1 \cos{(ta/2)} +c_1 i \sin{(ta/2)}+c_2 \cos{(ta/2)} -c_2 i \sin{(ta/2)}\right)\right] \nonumber\]
\[\theta(t)=e^{-\gamma t/2}\left[(c_1+c_2) \cos{(ta/2)} +(c_1-c_2) i \sin{(ta/2)}\right] \nonumber\]
and grouping and re-naming constants:
\[\theta(t)=e^{-\gamma t/2}\left[c_3 \cos{(ta/2)} +c_4\sin{(ta/2)}\right] \nonumber\]
We will now evaluate \(c_3\) and \(c_4\) from the initial conditions. Let’s assume again that \(\theta(0)=\theta_0\) and \(\theta'(0)=0\). Evaluating the previous equation at \(t=0\):
\[\theta(0)=c_3=\theta_0 \nonumber\]
so we have
\[\theta(t)=e^{-\gamma t/2}\left[\theta_0 \cos{(\frac{ta}{2})} +c_4\sin{(\frac{ta}{2})}\right] \nonumber\]
\[\theta'(t)=e^{-\gamma t/2}\left[-\frac{\theta_0 a}{2} \sin{(\frac{ta}{2})} +\frac{c_4 a}{2}\cos{(\frac{ta}{2})}\right]-\frac{\gamma}{2}e^{-\gamma t/2}\left[\theta_0 \cos{(\frac{ta}{2})} +c_4\sin{(\frac{ta}{2})}\right] \nonumber\]
\[\theta'(0)=c_4\frac{a}{2}-\theta_0\frac{\gamma}{2}=0 \nonumber\]
\[c_4=\frac{\gamma \theta_0}{a} \nonumber\]
and therefore
\[\theta(t)=e^{-\gamma t/2}\left[\theta_0 \cos{\left(\frac{ta}{2}\right)} +\frac{\gamma \theta_0}{a}\sin{\left(\frac{ta}{2}\right)}\right] \nonumber\]
\[ \theta(t)=\theta_0 e^{-\gamma t/2}\left[ \cos{\left(\frac{ta}{2}\right)} +\frac{\gamma }{a}\sin{\left(\frac{ta}{2}\right)}\right]\]
If everything went well this equation should simplify to Equation \ref{eqn3} for the case \(\gamma=0\). Recall that \(a=\sqrt{4g/l-\gamma^2}\), so if \(\gamma=0\):
\[\theta(t)=\theta_0 \left[ \cos{\left(\frac{ta}{2}\right)}\right] \nonumber\]
\[\theta(t)=\theta_0 \left[ \cos{\left(\sqrt{\frac{g}{l}}t\right)}\right] \nonumber\]
This of course does not prove that our solution is correct, but it is always good to see that we recover a known equation for a particular case (in this case \(\gamma=0\)).
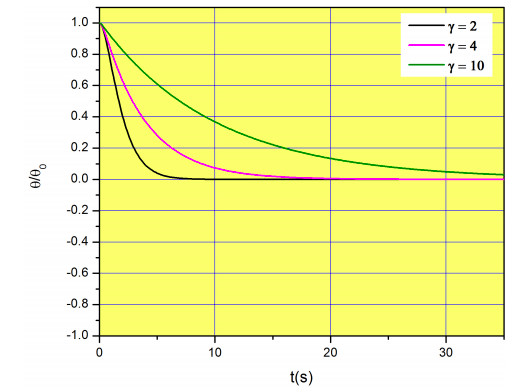
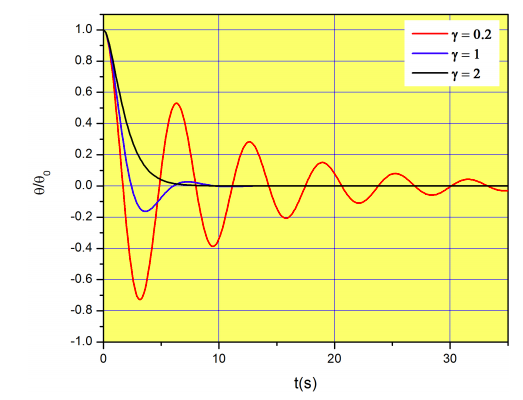
Figure \(\PageIndex{3}\) shows \(\theta(t)/\theta_0\) for three cases with \(g/l=1\) (i.e. a cord of length 9.8 m) and increasing values of friction. Remember that we are assuming that \(\theta\) is small.
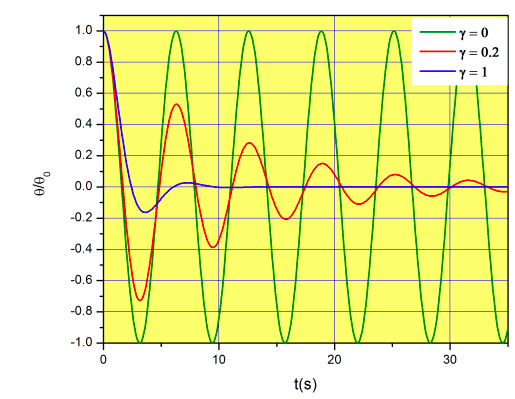
So far we have analyzed the case \(\gamma^2<4g/l\). As we increase the friction coefficient, we will reach the point where \(\gamma^2=4g/l\). Look at Figure \(\PageIndex{3}\), and think about what you would see when this happens. Mathematically, we will have two repeated roots:
\[\alpha_{1,2}=\frac{-\gamma \pm\sqrt{\gamma^2-4g/l}}{2}=-\frac{\gamma }{2} \nonumber\]
so \(\theta(t)=e^{-\gamma t/2}\) is a solution, but we need to find an independent solution through the method of reduction of order. We know that the general solution will be (Section 2.2):
\[\theta(t)=(c_1+c_2 t)e^{-\gamma t/2} \nonumber\]
The arbitrary constants will be calculated from the initial conditions:
\[\theta(0)=(c_1)=\theta_0 \nonumber\]
\[\theta'(t)=-\frac{\gamma}{2}(\theta_0+c_2 t)e^{-\gamma t/2}+c_2e^{-\gamma t/2} \nonumber\]
\[\theta'(0)=-\frac{\gamma}{2}(\theta_0)+c_2=0 \nonumber\]
\[c_2=\frac{\gamma}{2}\theta_0 \nonumber\]
Therefore,
\[\theta(t)=(c_1+c_2 t)e^{-\gamma t/2} \nonumber\]
\[\theta(t)=(\theta_0+\frac{\theta_0 \gamma}{2} t)e^{-\gamma t/2}=\theta_0(1+\frac{\gamma}{2} t)e^{-\gamma t/2} \nonumber\]
The behavior of \(\theta(t)\) is shown in Figure \(\PageIndex{4}\) in black. This regime is called critically damped because it represents the point where the oscillations no longer occur as \(\gamma\) increases. If we continue increasing the frictional coefficient, the pendulum will approach \(\theta=0\) slower and slower, but will never cross to the other side (\(\theta<0\)). Let’s find the mathematical expression for \(\theta(t)\) for the case \(\gamma^2>4g/l\). The two roots are now different and real:
\[\alpha_{1,2}=\frac{-\gamma \pm\sqrt{\gamma^2-4g/l}}{2} \nonumber\]
and the general solution is therefore
\[\theta(t)=c_1e^{\alpha_1t}+c_2e^{\alpha_2t} \nonumber\]
\[\theta(t)=c_1e^{(-\gamma+b)t/2}+c_2e^{(-\gamma-b)t/2}; \; b=\sqrt{\gamma^2-4g/l} \nonumber\]
The first initial condition is \(\theta(0)=\theta_0\):
\[\theta(0)=c_1+c_2=\theta_0 \nonumber\]
The second initial condition is \(\theta'(t)=0\):
\[\theta'(t)=c_1\left(\frac{-\gamma+b}{2}\right)e^{(-\gamma+b)t/2}+c_2\left(\frac{-\gamma-b}{2}\right)e^{(-\gamma-b)t/2} \nonumber\]
\[\theta'(0)=c_1\left(\frac{-\gamma+b}{2}\right)+c_2\left(\frac{-\gamma-b}{2}\right)=0\nonumber \]
\[\theta'(0)=-(c_1+c_2)\gamma+(c_1-c_2)b=0 \nonumber\]
the first initial condition yielded \(c_1+c_2=\theta_0\) so
\[\theta'(0)=-\theta_0\gamma+(c_1-c_2)b=0 \nonumber\]
\[(c_1-c_2)=\theta_0\gamma/b \nonumber\]
The two initial conditions gave two relationships between \(c_1\) and \(c_2\):
\[c_1+c_2=\theta_0 \nonumber\]
\[(c_1-c_2)=\theta_0\gamma/b \nonumber\]
Solving this system of two equations with two unknowns:
\[c_1=\frac{\theta_0}{2}\left(1+\frac{\gamma}{b} \right) \nonumber\]
\[c_2=\frac{\theta_0}{2}\left(1-\frac{\gamma}{b} \right) \nonumber\]
And finally we can write the particular solution as:
\[\theta(t)=c_1e^{(-\gamma+b)t/2}+c_2e^{(-\gamma-b)t/2}; \; b=\sqrt{\gamma^2-4g/l} \nonumber\]
\[\theta(t)=\frac{\theta_0}{2}\left(1+\frac{\gamma}{b} \right)e^{(-\gamma+b)t/2}+\frac{\theta_0}{2}\left(1-\frac{\gamma}{b} \right)e^{(-\gamma-b)t/2}; \; b=\sqrt{\gamma^2-4g/l} \nonumber\]
\[ \theta(t)=\frac{\theta_0}{2}e^{-\gamma t/2}\left[\left(1+\frac{\gamma}{b} \right)e^{b t/2}+\left(1-\frac{\gamma}{b} \right)e^{-b t/2}\right]\]
Figure \(\PageIndex{5}\) shows results with \(g/l=1\), and three different values of \(\gamma\). Notice that \(\gamma=2\) corresponds to the critically damped regime.