4.E: Exercises
- Page ID
- 41330
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Q4.9
What is the entropy changed when 10.2 moles of diatomic gas is cooled from a temperature of 25 °C to 10 °C at constant pressure?
Q4.9
Determine the value of 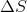 while reversibly heating 5 moles of an ideal gas from 25 °C to 73 °C at constant volume.
while reversibly heating 5 moles of an ideal gas from 25 °C to 73 °C at constant volume.
S4.9
At constant volume, dqrev = CV dT.
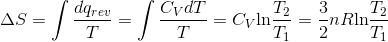
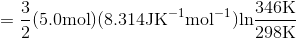
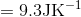
Q4.10
If 1.50 moles of an ideal gas were compressed isothermally from 6.6 L to 2.5 L:
- What is
Ssys when compressed irreversibly?
Ssys when done reversibly?
- What do the values mean for the overall process?
S4.10
- \(\bigtriangleup S_{sys}=nR\ln\dfrac{V_2}{V_1}\rightarrow \bigtriangleup S_{sys}=(1.5mol)(8.314\dfrac{L\cdot atm}{mol\cdot K})(\ln\dfrac{2.5L}{6.6L})=-12.1 \dfrac{kJ}{mol}\)
- The change in entropy of the system is the same whether an irreversible or reversible process is being carried out.
- The negative value means that the reaction that was carried out was unfavorable. Entropy increases as molecules become more disordered.
Q4.13
Nitrogen gas is reversibly heated at constant pressure of 101.3 kPa. The molar heat capacity of nitrogen gas is:
Cp = A + BT + CT2, where A = 27.4 J/mol-K, B = 5.23 x 10-3 J/mol-K2, and C = -0.0300 x 10-7 J/mol-K3.
Assuming N2 is an ideal gas, calculate the change in entropy when 42 g of N2(g) is heated from 250 K to 350 K.
Q4.21
Imagine you are to carry out the isothermal and reversible gas expansion with an ideal gas. You have 0.5 moles of the gas at 280K. You wish to expand this gas from its initial volume of 2 liters to a new volume of 8 liters. What would your values for heat, work, change in entropy, and change in internal energy have to be? What if you wanted to instead carry his experiment out as isothermal and irreversible with 2.0 atm of external pressure?
Q4.22
Consider 0.50 moles of an ideal gas at 30oC. It expands from a pressure of 4.5 atm to a pressure of 2.0 atm at the same temperature.
- For a reversible process, find the entropy change for the surrounding.
- For an irreversible process, calculate the entropy change for the universe which against a constant external pressure of 2.0 atm.
S4.22
a) Reversible process:
delta S of system =(\dfrac{q}{T}\)=(\dfrac{-W}{T}\)=(\dfrac{-1}{T}*(-nRT\ln\dfrac{V2}{V1})\)=(\nR\ln\dfrac{P1}{P}\)
qsys/T = - Wsys/T = -1/T *(-nRT\ln (V2/V1) = nR\ln (P1/P2)
= 0.5 moles * 8.3145 Jmol-1K-1 * \ln(4.5/2)
= 3.37 J/K
delta S of surrounding = -3.37 J/K
b) Irreversible process:
delta S of system is 3.37 J/K
Delta S(surrouding)=(\dfrac{-1}{T}*P2*V2*(1-\dfrac{V1}{V2})\)= (\-nR(1-\dfrac{P2}{P1})\)
delta S of surrounding = -1/T * P2*V2*(1 - V1/V2) = -nR(1 - P2/P1)
=-0.5 * 8.3145 *(1-2/4.5)=2.31 J/K
delta of the universe is : 3.37 J/K +2.31J/K=5.68 J/K
Q4.23
Calculate ΔSsys for the heating of 2.00 moles of nitrogen from 25ºC to 200ºC. The heat capacity of oxygen is:
Cp = (3.268 + 0.00325T) J K-1 mol-1
S4.23
\[\Delta S = \int n\dfrac{\bar{C_{P}}}{T}dT\]
\[\Delta S = \int_{(25+273)K}^{(200+273)K} (2 mol)\dfrac{(3.268 + 0.00325T)J \ mol^{-1} \ K^{-1}}{T}dT\]
\[\Delta S = \int_{298K}^{473K} (\dfrac{6.536}{T}+ 0.0065)J \ mol^{-1}dT\]
\[\Delta S = {(6.536}\ln(T)+ 0.0065T)_{298}^{473}J \ mol^{-1}\]
\[\Delta S = 4.16 J \ mol^{-1}\]
Q4.27
The value of 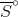 (CO2(aq)) is less than that of
(CO2(aq)) is less than that of 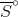 (CO2(g)) at 298 K. (Note: Refer to table below). Would this be the case at a temperature of 0 K as well?
(CO2(g)) at 298 K. (Note: Refer to table below). Would this be the case at a temperature of 0 K as well?
| Substance | 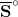 / J K-1 mol-1 / J K-1 mol-1 |
| CO2(g) | 213.6 |
| CO2(aq) | 117.6 |
S4.27
Since the gaseous form of a compound always has a greater enthalpy than the more ordered liquid or aqueous form, this would still be the case at a temperature of 0 K as well.
Q4.27
Is the standard entropy of CO2(g) higher than the standard entropy of CO2(s) at 298 K? What about at 0 K?
Q4.28
You have an ideal gas that expands 3.56 L with the initial volume at 22 L. All you know is that you have 0.45 moles and that the temperature is 22 ºC. What is the change in Gibbs free energy for this system?
S4.28
.gif?revision=1&size=bestfit&width=142&height=40)
.gif?revision=1&size=bestfit&width=93&height=39)
.gif?revision=1&size=bestfit&width=410&height=38)
=167.3
Q4.28
0.70 moles of an ideal gas expands adiabatically from 1.0 atm to 2.5 atm at a temperature of 30ºC. Calculate the values of q, w, U,
S, and
G.
S4.28
\(q=0\) \(w=-nRT\ln\dfrac{P_1}{P_2}=-(.70mol)(8.314\dfrac{J}{mol\cdot K})(303K)(\ln\dfrac{1.0atm}{2.5atm})(\dfrac{1kJ}{1000kJ}=1.62\dfrac{kJ}{mol}\)
\(\bigtriangleup U=w=1.62\dfrac{kJ}{mol}\)
\(\bigtriangleup S_{univ}=\bigtriangleup S_{sys}=nR\ln\dfrac{P_1}{P_2}=(.70mol)(8.314\dfrac{J}{mol\cdot K})\ln\dfrac{1.0atm}{2.5atm}=-5.33\dfrac{J}{mol}\)
\(dH=VdP\rightarrow \dfrac{dH}{dP}= nRT\ln\dfrac{P_2}{P_1}=(.70mol)(8.314\dfrac{J}{mol\cdot K}(303K)(\ln\dfrac{2.5atm}{1.0atm}(\dfrac{1kJ}{1000J}\)
\(=1.62\dfrac{kJ}{mol}\)
\(\bigtriangleup G= \bigtriangleup H- T\bigtriangleup S= 1.62 \times 10^3\dfrac{J}{mol}-(303K)(-5.33\dfrac{J}{mol/cdot K}=3234\dfrac{J}{mol}\)
\(=3.23\dfrac{kJ}{mol}\)
Q4.30
Use the values listed listed below to calculate the value of ΔrG° for the following reaction:
pyruvate(aq) → 2 lactate ion(aq) + 2H+(aq)
(ΔfG°[pyruvate(aq)] = -472.4 kJ mol-1, ΔfG°[lactate ion] = -516.7 kJ mol-1). Is pyruvate or the lactate ion favored under standard conditions? Explain.
Q4.30
Use the values listed listed below to calculate the value of ΔrG° for the following reaction:
pyruvate(aq) → 2 lactate ion(aq) + 2H+(aq)
(ΔfG°[pyruvate(aq)] = -472.4 kJ mol-1, ΔfG°[lactate ion] = -516.7 kJ mol-1)
Q4.31
A scientist measures studies the thermodynamics of a protein of interest. He interested in finding the Free Energy of unfolding in the quaternary structure of protein at a concentration of 5µM. He finds that the Gibbs free energy of the reaction -0.84 Kcal/mol. Why does the scientist want to know the value of (\Delta G\) Explain how the reaction proceeds.
S4.31
The value of (\Delta G\) of the reaction will let the scientist know how likely the reaction of the unfolding of the protein is to occur. If (\Delta G\) is negative the reaction will go forward, towards the unfolded state. In this case (\Delta G\) is negative so the reaction goes forward to the unfolding of the protein.
Q4.32
For the reaction
\[H_{2 (g)} + Cl_{2 (g)} \rightarrow 2HCl_{(g)}\]
Using the formula ∆rG = ∆fG (products)-∆fG (reactants) to compute the Gibbs energy of the reaction?
Q4.34
Consider the conversion of graphite carbon into diamond
\[C_{(graphite)}\rightarrow C_{(diamond)}\]
- Determine \(\Delta rH^o\) and \(\Delta rS^(o)\) for the reaction. Is the conversion spontaneous at any temperature?
- The molar volume of graphite is \(2.1cm^3\) greater than diamond in density.
- If you apply pressure on graphite at \(25^{o}C\), can you convert graphite to diamond? If so, determine the required pressure to make the process spontaneous.
S4.34
(a)
$$\Delta rH^{o}=\Delta _f\bar{H}^{o}[C_{(diamond)}]-\Delta _f\bar{H}^{o}[C_{(graphite)}]\]
$$=1.90Kjmol^{-1}-0kjmol^{-1}\]
$$=1.90kj\,mol^{-1}\]
$$\Delta rS^{o}=\Delta S^{o}[C_{(diamond)}]-\Delta S^{o}[C_{(graphite)}]\]
$$=2.4J\,K^{-1}mol^{-1}-5.7JK^{-1}mol^{-1}\]
$$=-3.3J\,K^{-1}mol^{-1}\]
At \(0^oC\),
$$\Delta rG^{o}=\Delta rH^o-(273K)\Delta rS^{o}\]
$$=(1.90kj\,mol^{-1})-(273K)(-3.3\times10^{-3}kj\,K^{-1}mol^{-1})\]
$$=2.8834kj\,mol^{-1}\]
(b)
Step 1:
$$G_2=G_1+V(P_2-P_1)\]
Step 2: (Hint: Apply molar quantities)
$$\bar{G}_2=\bar{G}_1+\bar{V}\Delta P\]
Step 3: (Hint: Apply the equation to diamond and graphite)
$$\bar{G}_2[Graphite]=\bar{G}_1[graphite]+\bar{V}[graphite]\Delta P\]
$$\bar{G}_2[diamond]=\bar{G}_1[diamond]+\bar{V}[diamond]\Delta P\]
Step 4: (Hint: Combine the equations)
$$\Delta rG_2=\Delta rG_1+[\bar{V}[diamond]-\bar{V}[graphite]]\Delta P\]
Step 5: (Hint: At \(25^oC,P_1=1bar\; so\; \Delta rG_1=\Delta rG^o=2.883kj\,mol^{-1}\))
$$\Delta rG_2=2.883kj\,mol^{-1}+(-2.1cm^3mol^{-1})\Delta P(\dfrac{1L}{1000cm^{3}})(\dfrac{1atm}{1.01 bar})(\dfrac{101.3J}{1L\,atm})(\dfrac{1kj}{1000J})\]
$$\Delta rG_2=2.883kj\,mol^{-1}-2.1\times10^{-4}\Delta P\,kj\,bar^{-1}mol^{-1}\]
Step 6: (Hint: To make the process spontaneous)
$$\Delta rG_2=2.883kj\,mol^{-1}-2.1\times10^{-4}\Delta P\,kj\,bar^{-1}mol^{-1}\lt0\]
$$2.883kj\,mol^{-1}\lt2.1\times10^{-4}\Delta P\,kj\,bar^{-1}mol^{-1}\]
$$\Delta P\lt\dfrac{2.883kj\,mol^{-1}}{2.1\times10^{-4}}=1.4\times10^{4} bar\]
Q4.36
Predict the signs of \(\Delta H,\Delta S\) and \(\Delta G\) of the system for the following processes at 1atm:
- Ice melt at 200 K
- Ice melt at 273.15 K
- Ice melt at 300 K
S4.36
\(\Delta H\) is positive for all because melting is endothermic. \(\Delta S\) is positive for all because going from solid to liquid is becoming more disordered. \(\Delta G\) for (a) is positive because reaction is not spontaneous when melting at below the melting point, \(\Delta G\) for (b) is 0 because reaction is in equilibrium at the melting point, \(\Delta G\) for (c) is negative because reaction is spontaneous when melting at above the melting point.
| (a) | (b) | (c) | |
| \(\Delta H\) | + | + | + |
| \(\Delta S\) | + | + | + |
| \(\Delta G\) | + | 0 | - |
Q4.37
Crystals of AgCl(s) form spontaneously when aqueous solutions of silver(I)nitrate and sodium chloride are combined. What can you deduce about the signs of the changes in enthalpy and entropy?
Q4.38
The formation reaction to form magnesium oxide is as follow:
\[ \ce{Mg(s) + 1/2 O_2 (g) \rightarrow MgO(s) }\]
Verify the equation ΔG° = ΔH° + TS° using values from Appendix
Hint: Gibbs free definition above is free energy of the whole reaction, not free energy of formation
S4.38
\[\Delta_{r}\bar{G}^{\circ} = \sum \Delta_f\bar{G}^{\circ}[products] - \sum \Delta_f\bar{G}^{\circ}[reactants] = -569.5 \dfrac{kJ}{mol} -0-0 = {\color{red}-569.5 \dfrac{kJ}{mol}}\]
\[\Delta_{r}\bar{H}^{\circ} = \sum \Delta_f\bar{H}^{\circ}[products] - \sum \Delta_f\bar{H}^{\circ}[reactants] = -601.8 \dfrac{kJ}{mol} -0-0 = -601.8 \dfrac{kJ}{mol} \]
\[\Delta_{r}\bar{S}^{\circ} = \sum \Delta_{f}\bar{S}^{\circ} [products] - \sum \Delta_{f}\bar{S}^{\circ} [reactants] = (26.78 - 32.68 - \dfrac{205.0}{2})\dfrac{J}{mol \cdot K} = -108.4 \]
\[\Delta_{r}\bar{H}^{\circ} - T\Delta_{r}\bar{S}^{\circ} = -601.8 \dfrac{kJ}{mol} - (298K)(-0.1084 \dfrac{kJ}{mol \cdot K}) = {\color{red}-569.5 \dfrac{kJ}{mol}}\]
The answers agree therefore the equation is true.
Q4.39a
At 49ºC, a particular reaction is spontaneous. What would be the smallest possible value of ΔrS for the reaction if ΔrH was 10 kJ?
S4.39a
Use the following equation
\[ \Delta G = \Delta H - T \Delta S\]
Since the process is spontaneous:
Note: Don't forget to flip the inequality when dividing by a negative number.
\[ \begin{align} \Delta G &< 0 \\ \Delta H - T \Delta S &< 0 \\ (10 \ kJ) - (322 \ K) \Delta S &< 0 \\ - (322 \ K) \Delta S &< 10 \ kJ \\ \Delta S &>0.031 \end{align}\]
Thus the minimum value is the closest number above 0.031 kJ K-1.
Click here for more information on Gibb's free energy.
Q4.39b
Calculate the minimum change in entropy of reaction for a spontaneous process at 340K with an enthalpy change of reaction equal to 800 J. Your answer must be in KJ/K and have 2 significant figures.
Q4.39c
The entropy change for a reaction is found to be 47.50 J/K. The enthalpy change for the reaction is 21.25 KJ. At what temperature is this reaction spontaneous?
S4.39c
\[\Delta _{r}G=\Delta _{r}H-T\Delta _{r}S\]
Because we want to find the temperature at equilibrium we set the Gibbs Free Energy equal to 0. Thus:
\[\Delta _{r}H=T\Delta _{r}S\]
\[T=\frac{\Delta _{r}H}{\Delta _{r}S}=\frac{21.25\times 10^{3}J}{47.50\frac{J}{K}}=447.4K\]
Q4.40a
The standard Gibbs energy change, ∆rGo, for the reaction is +108 kJ. What can you deduce about the state of reaction when the reactants are mixed together?
S4.40a
When the two gases are mixed, there is no interaction between them. So, the products would not form.
Q4.40b
A scientist mixes together a set of reagents which are known to undergo a reaction with a negative change in Gibbs’ free energy in a beaker. When the scientist comes back in a few hours, they find by looking at the beaker that the reaction does not appear to have proceeded. What are two reasons that the scientist would not observe a change after two hours?
S4.40b
The Gibbs' free energy is an indicator of a reaction's favorability, but does not indicate that that reaction will proceed quickly. If the rate constant for the reaction is low, or the concentration of one or more of the reagents is low, the reaction might not proceed at a pace that the scientist would observe over a few hours or even longer.
Q4.41
If water changes from a liquid to a gas at 50ºC and 0.123 bar, what must the pressure be to convert water from a liquid to a gas at 75ºC? The molar enthalpy of vaporization for water (ΔvapH) is 42.3 kJ mol-1
S4.41
\[\ln \left( \dfrac{P_{2}}{P_{1}} \right) = \dfrac{\Delta \bar{H}_{vap}}{R} \left( \dfrac{1}{T_{1}}-\dfrac{1}{T_{2}} \right) \]
\[T_1= \left( 50 + 273 \right) K = 323\,K\]
\[T_2 = \left( 75 + 273 \right) K= 348\,K\]
\[\ln \left( \dfrac{P_{2}}{0.123\,bar} \right) = \dfrac{42.3\times 10^3\,J mol^{-1} }{8.314 J \ mol^{-1} \ K^{-1}} \left( \dfrac{1}{323\,K}-\dfrac{1}{348\,K} \right) \]
\[\ln \left( \dfrac{P_{2}}{0.123\,bar} \right) = 1.132\]
\[\dfrac{P_{2}}{0.123\,bar} = 3.10\]
\[P_{2}= 0.381 \,bar\]
Q4.42
What is the change in pressure when ice melts ast room temperature if the density of ice is 0.919 g/ml and the ΔfusH = 6.01 KJ/mol?
Q4.42
Calculate the freezing point depression of ice if a pressure of 450 atm is exerted on it by a car that weighs 1500-kg. Note: The molar volumes are as follows: molar volume of liquid water is 18.03 mL mol-1 and the molar volume of ice is 19.65 mL mol-1.
S4.42
Use the slope of the S-L curve from the phase diagram:
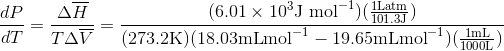
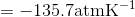
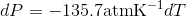
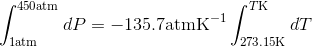
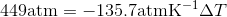
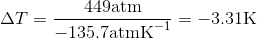
This means that the freezing point depression determined for when 450 atm of pressure is applied to ice by a car is 3.30 K.
Q4.43
Here is a phase diagram for carbon.
- What phase will carbon be if temperature is increased at constant pressure from the triple point between the vapor, liquid, and graphite?
- At 1.0 GPa and 5000 K, what phase will carbon be in?

S4.43
- Carbon will be in its vapor phase if the temperature is increased from the lower triple point.
- At 1.0 GPa and 5000 K, carbon will be in the liquid phase.
Q4.46
Look at the phase diagram of water. Which phase is more dense, liquid or solid? How can you tell by just looking at the graph?
The link below contains a phase diagram of water:
S4.46
Through looking at the phase diagram, we can see that the liquid phase is more dense. You can see this because the line separating the two phases is negative.
Q4.48
Explain what happens to ΔvapH as the temperature increases significantly.
Q4.49
You go on an adventure and find yourself stranded on the top of a mountain where the air pressure is 0.68 atm. You find water but you want to make sure is safe to drink so you want to boil the water. At what temperature would you expect the water to start boiling? Hint: The molar heat of vaporization of H2O is 41.0 kJ mol-1
Q4.50
At higher altitude, water is boiled faster than at lower altitude. The reason is because the pressure is smaller. Given the heat of vaporization of water at 100oC is 42.0 KJ/mol. Calculate the temperature to boil the water at a place where air pressure is 0.7 atm?
Q4.52
The equations are as follows
- \(dS=\dfrac{CpdT}{T}\)
- \(\Delta S=\dfrac{\Delta H }{T}\)
- \(S_0=0\)
- \(dS=\dfrac{dq}{T}\)
Determine the conditions needed for each equation.
S4.52
- Constant pressure
- Constant pressure and temperature
- Absolute 0, no residual entropy, pure crystalline
- reversible process
Q4.54
Calculate the entropy change when nitrogen gas is heated from 25°C to 75°C while simultaneously allowed to expand from 0.562 L to 1.245 L. Assume ideal gas behavior.
S4.54
1. Find how many moles of gas we have: \(PV=nRT\)
\[n=\dfrac{PV}{RT}=\dfrac{1 atm*0.562L}{(0.08206L*atm/K*mol)(298.15K)}=0.02297mol \]
2. entropy change during expansion:
\[Delta S=nR\ln{\dfrac{V_2}{V_1}}=(0.02297mol)(8.314J/K*mol)\ln{\dfrac{1.245L}{0.562L}}=0.1519J/K\]
3. entropy change during heating at constant volume:
\[\begin{align*}\Delta S&=n\bar{C}_v\ln{\dfrac{T_2}{T_1}}=n(\dfrac{5}{2}R)\ln{\dfrac{T_2}{T_1}}\\
&=(0.02297mol)(\dfrac{5}{2})(8.314J/K*mol)\ln{\dfrac{348.15K}{283.15K}}=0.0987J/K\end{align*}\]
4. Combine 2&3:
\[\Delta S_{tot}=\Delta S_{expansion}+\Delta S_{heating}=0.1519J/K+0.0987J/K=0.2506J/K\]
Q4.54
A \(4 \times 10^{-2}\) moles sample of Xenon (Xe) is heated from 300 K to 400 K in a 1 L container at 1.5 atm. What will be the change in entropy if Xe is able to expand to twice the volume of the container?
Q4.55
Photosynthesis depends upon the absorption of visible light. However, the infrared radiation can not be used for photosynthesis. Explain why.
S4.55
The infrared light : Cells do absorb the photon of infrared radiation, but it could not provide enough energy to do work in a biological system.
Whereas, for the visible light, each photon of visible light contains just enough energy to excite the electrons of molecules.
Photosynthesis is carried out by using the visible light.
Q4.56a
An amount of ideal diatomic gas is expanded from 4.8 atm to 1.7 atm while experiencing the change of temperature from 35°C to 128ºC. The change in entropy of the gas expansion process is 15.0 J/K. Determine the ΔU, ΔH, and ΔS of the entire process. Assume the temperature is not enough to unleash the rotational and vibrational energy of the gas.
Hint: Break the problem into 2 processes (isothermic and isobaric)
S4.56a
Step 1: Consider the isothermal process of the ideal gas (expanding from 4.8 atm to 1.7atm at constant temperature of 35°C
ΔU = 0, ΔH = 0, ΔS = 15.0 J/K
\[\Delta S = nRln\dfrac{V_2}{V_1} = nRln\dfrac{P_1}{P_2}\]
\[n = \dfrac{\Delta S}{Rln\dfrac{P_1}{P_2}} = \dfrac{15.0 \dfrac{J}{K}}{( 8.314 \dfrac{J}{mol \cdot K})ln\dfrac{4.8 atm}{1.7 atm}} = 1.738 moles\]
Step 2: Consider the change in temperature at constant pressure of 1.7 atm
\[\Delta H = C_p \Delta T = \dfrac{7}{5}nR\Delta T = \dfrac{7}{5} (1.738 moles)(8.314\dfrac{J}{K\cdot mol})(128-35)K = 1.88 \times 10^{3} J\]
\[\Delta U = \Delta H - nR\Delta T = (1.88 \times 10^{3} J ) -(1.738 moles)(8.314 \dfrac{J}{K \cdot mol})(128-35)K = 537 J\]
\[\Delta S = C_p ln\dfrac{T_2}{T_1} = \dfrac{7}{5}nRln\dfrac{T_2}{T_1} = \dfrac{7}{5}(1.738 moles)(8.314 \dfrac{J}{K \cdot mol})ln\dfrac{(128+273)K}{(35+273)K} = 5.34 \dfrac{J}{K}\]
For the entire process
\[ \Delta H = 0 J + 1.88 \times 10^3 J = {\color{red}1.88 \times 10^3 J} \]
\[ \Delta U = 0 J + 537 J = {\color{red}537 J} \]
\[ \Delta S = 15.0 \dfrac{J}{K} + 5.34 \dfrac{J}{K} = {\color{red}20.34 \dfrac{J}{K}} \]
Q4.56b
Calculate the ΔU, ΔH, and ΔS of 3.00 moles of an ideal monatomic gas that are compressed from 7.00 L to 1.00 L while being heated from 25 ºC to 100 ºC.
S4.56b
Break the process down into two steps: isothermal compression from 7 L to 1 L at 298 K and heating at a constant pressure from 298 K to 373 K.
a. Compression:
Because the compressions is isothermal, ΔU=0 & ΔH=0 for this step
\[\Delta S = nR\ln(\dfrac{V_{2}}{V_{1}})=(3mol)(8.314J\ mol^{-1}\ K^{-1})\ln(\dfrac{1}{7})\]
\[\Delta S = -48.5 J \ K^{-1}\]
b. Heating:
\[\Delta H = C_{P}\Delta T = \dfrac{5}{2}nR\Delta T=\dfrac{5}{2}(3 mol)(8.314 J\ mol^{-1}\ K^{-1})(373-298)K\]
\[\Delta H = 4677 J\]
\[\Delta U = \Delta H - nR\Delta T = 4677 J - (3mol)(8.314 J\ mol^{-1}\ K^{-1})(373-298)K\]
\[\Delta U = 2806 J\]
\[\Delta S = C_{P}\ln(\dfrac{T_{2}}{T_{1}}) = \dfrac{5}{2}nR\ln(\dfrac{T_{2}}{T_{1}})\]
\[\Delta S = \dfrac{5}{2}(3mol)(8.314 J\ mol^{-1}\ K^{-1})\ln(\dfrac{373}{298}) = 14.0 J \ K^{-1}\]
c. For entire process
\[\Delta H = 0J + 4677 J= 4.68kJ\]
\[\Delta U = 0J+ 2806 J=2.81kJ\]
\[\Delta S = -48.5 J \ K^{-1}+14.0 J \ K^{-1} = -34.5 J \ K^{-1}\]
Q4.57a
Briefly provide examples and descriptions for each of the three laws of thermodynamics.
S4.57a
- The first law is the conservation of mass and energy. Basically you can't create anything out of thin air and perpetual motion machines are impossible.
- The second law states how entropy is always increasing and the entropy of the universe can never become negative. In other words things will always attempt to go to equilibrium. This is seen commonly when batteries run out. You never see a battery charge itself spontaneously because that would violate the second law.
- The third law states how a pure crystalline structure at 0 K will essentially have 0 entropy. The third law is visualized by knowing how frozen and solid materials have less entropy because the molecules within can only vibrate.
Q4.57b
The three laws of thermodynamics are often generally stated to be:
- Energy and matter cannot be created or destroyed.
- The entropy of the universe is always increasing.
- At absolute zero, the entropy of a system is zero.
With this knowledge, which of the three laws of thermodynamics apply to the examples below? There may be more than one.
a.) A graduate student in UC davis claims to have created the world's first perpetual motion engine. This machine produces no heat and can be used, (he claims), to power the campus for the next decade! This is not possible.
b.) .gif?revision=1&size=bestfit&width=100&height=45)
If TF becomes 0, entropy becomes undefined. Hence, it is not possible to reach absolute zero.
c.) In an adiabatic gas expansion where:
\[\Delta U=Q+w\]
No thermal energy or matter is exchanged. Hence:
\[\Delta U=w\]
d.) In an imperfect crystal of CO, carbon monoxide, there are multiple energy states at 0K. Thus, it experiences residual entropy and, quite unusually, follows:
\[\lim _{T\to0K}S>0\]
S4.57b
a.) first and second laws; The existence of the perpetual motion machine violates the first and second laws of thermodynamics. Because
\[\Delta U=Q+w\]
and heat is a form of entropy, a perpetual motion machine does not increase the entropy of the universe. By definition, a machine which does work must do less work than it has internal energy.
b.) second and third law; In order for absolute zero to be reached, the system would have to be removed from the universe. Because
\[\Delta S=n\bar{C}_{p}ln\left ( \frac{T_{2}}{T_{1}} \right )\]
and entropy must always increase, a system within the universe would always be at a temperature lower than its surroundings and hence could experience heat transfer which would mitigate the absolute zero condition.
c.) first law; Energy which is "lost" from the system due to lack of heat transfer is compensated by the system doing more work.
d.) third law; In a perfect crystal, where there is only one energy state, there is no residual entropy at 0K
Q4.58
The standard enthalpy of formation of ice is -291.83 kJ/mol and its standard molar entropy is 41.0 J/(mol K). The standard enthalpy of formation of liquid water is -285.83 kJ/mol and its standard molar entropy is 69.95 J/(mol K). Estimate the melting point of water based on this information. What would you expect the value be? Do your values match? What assumptions made during this calculation could be responsible for the difference?
Q4.61
In a reversible adiabatic expansion, what do you expect to happen to the volume? What about the temperature?
S4.61
We expect both volume and temperature to increase.
Q4.63
Aniline can hydrogen bond, whereas benzene is nonpolar. Explain why, contrary to our expectation, benzene melts at a higher temperature than aniline. Why is the boiling point of aniline higher than that of benzene?
Q4.64
Molar Gibbs energies of solid, liquid and vapor depend on temperature and pressure. (a) Briefly explain how temperature affects molar Gibbs energy. (b) Explain how pressure changes affect molar Gibbs energy. Why is water an exemption?
S4.64
- At a constant pressure the phase with the lowest molar Gibbs energy is the most stable phase at that temperature. At high temperatures the vapor phase has the lowest molar Gibbs energy, therefore it is the most stable. As temperature decreases, liquid becomes the stable phase, and at even lower temperatures, solid becomes the most stable phase.
- From the equation \(\left (\dfrac{\partial \Delta G}{\partial P} \right )=\bar{V}\) we observe that the molar volume affects the molar Gibbs energy depending on pressure. In this case the vapor phase has the greatest increase in molar Gibbs energy because the molar volume is much larger than that of liquids and solids. In general, an increase in external pressure will raise both the melting point and the boiling point of a substance. The exception to this, is water. This is because the molar volume of ice is actually greater than that of liquid water. Thus, for water an increase in pressure will lower the melting point.
Q4.65
When ice melts to liquid water, entropy is increasing and the the surrounding becomes cooler since ice absorbs heat. Explain the relationship between those two facts.
Q4.66
For any spontaneous endothermic process, what must be true about the entropy of the process?
Q4.67
For the following situation take a rubber band and stretch it quickly. It will feel warm. Next stretch it out for a few seconds and then release it. Consequently, it will feel cool. Why do you think this happens? Explain thermodynamically.
S4.67
\[\Delta G =\Delta H-T\Delta S\]
The warming effect: Stretching the rubber band creates a nonspontaneous process \((\Delta G\gt0)\) and \(-(\Delta G\lt 0)\). The warming effect means that \(\Delta H\lt0)\). This makes \(\Delta S\) negative. T must be positive and \(\Delta S\) must be negative. This tells us that the rubber band under tension is more disordered in its natural state.
The cooling effect: If theres no tension and the rubber band snaps back to its natural state, \(\Delta G\) is negative and \(-\Delta G\) is positive. Since it cools the \(\Delta H\gt0\) so \(T\Delta S\) is positive. Entropy increases when the rubber band goes from stretched state to natural state.
Q4.69
Cold packs utilizes the chemical reaction of water and ammonium nitrate (or similar substances) to turn cold. Predict the signs of \(\Delta H, \Delta S\) and \(\Delta G\) for the reaction when the membrane that separates the two substances in a cold pack breaks.
S4.69
The reaction is spontaneous so \(\Delta G\) is negative; the cold pack feels cold because it's taking in heat so \(\Delta H\) is positive; \(\Delta S\) is positive because disorder increases as ammonium nitrate breaks down to ammonium ion and nitrate ion.
Q4.71
At what temperature will toluene have a vapor pressure of 517 torr. The normal boiling point of toluene is 110.6°C with the molar enthalpy of vaporization being 35.2 kJ/mol. (Hint: Use Clausius-Clapeyron equation).
S4.71
\[ ln\dfrac{P_2}{P_1} = \dfrac{\Delta _vap \bar H}{R} (\dfrac{1}{T_2} - \dfrac{1}{T_1}) \]
\[ ln\dfrac{517 torr}{760 torr} = \dfrac{35.2 \times 10^3 \dfrac{J}{mol}}{8.314 \dfrac{J}{K \cdot mol}} (\dfrac{1}{T_2} - \dfrac{1}{(110.6+273)K}) \]
\[ \Rightarrow {\color{red}T_2 = 397.5 K = 124^{\circ}C} \]
Q4.72a
You have discovered a way to create a new organic compound of the formula \(C_xH_yN_zO_α\). What measurements would you need to take to find out values for the following:properties:
\[ \triangle_{f}\overline{H}^{\circ} = \ ? \ \ \triangle _{f}\overline{S}^{\circ} = \ ? \ \ \triangle _{f}\overline{G}^{\circ} = \ ?\]
S4.72a
For enthalpy, you need to take measurements of the change of enthalpy of one mole of the unknown compound. Thus you would need to take measurements for the molar heat capacity and how much temperature changes in for formation of one mole. See here and here.
For entropy of formation you would need to divide enthalpy by the temperature at which the formation takes place because the change in entropy can equate to enthalpy divided by temperature. See here.
For Gibb's free energy of formation, you simply need the enthalpy and entropy of formation along with the temperature where one mole of the substance is formed. See here.
\[ \Delta{G} = \Delta H - T \Delta S \]
Q4.72b
You are given hexane, C6H14, and a constant pressure calorimeter. What steps would you take to determine standard gibbs free energy of formation, .gif?revision=1&size=bestfit&width=34&height=17) for this substance?
for this substance?
Hint: .gif?revision=1) of hexane can be found using a measurement obtained by the calorimeter
of hexane can be found using a measurement obtained by the calorimeter
S4.72b
An equation for the complete combustion of hexane can be written as follows:
\[C_{6}H_{14(l)}+O_{2(g)}\rightarrow CO_{2(l)}+H_{2}O_{(l)}\]
The calorimeter would then be used to find the heat released by this reaction by the following rule:
\[\Delta _{r}H=-q_{P, calorimeter}=-\left ( C_{calorimeter} \Delta T\right )\]
after which the standard heat of formation for hexane could be calculated using the known heat of formation for H2O, O2, and CO2.
Under the 3rd law of dynamics, the standard entropy would then be calculated by
\[\Delta \bar{S}^{\circ}=-\frac{q_{rxn}}{T}\]
where T=298K
From this, standard entropy for the formation of hexane should be obtained from the known standard entropies of H2O, O2, and CO2, through the following reaction for the formation of hexane from elemental reactants:
\[6C_{(graphite)}+7H_{2(g)}\rightarrow C_{6}H_{14(l)}\]
The standard gibbs free energy of formation, .gif?revision=1&size=bestfit&width=34&height=17) for this substance is then determined through the relationship:
for this substance is then determined through the relationship:
\[\Delta _{f}\bar{G}^{\circ}=\Delta _{f}\bar{H}^{\circ}-T\Delta _{r}S^{\circ}\]
Q4.73
A 93.5 Liter drum at 65 C houses 20g of water. How many moles of water are in the vapor phase, and what mole fraction is in the vapor phase? The vapor pressure of water at 65C is 187.54 mmhg.
S4.73
\[\dfrac{PV}{/RT} = n\]
- ntot = 20g/18.02 g mol-1= 1.11 mol
- nvap = (187.54 mmhg 93.5 L)/(8.314 L atm mol-1 K-1* 338 K * 710 mmhg atm-1) = 8.79 *10-3 mol
- xvap= 8.79 *10-3 mol / 1.11 mol = 7.92*10-3

