25.1: Raoult's Law and Ideal Mixtures of Liquids
- Page ID
- 238275
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)This page deals with Raoult's Law and how it applies to mixtures of two volatile liquids. It covers cases where the two liquids are entirely miscible in all proportions to give a single liquid - NOT those where one liquid floats on top of the other (immiscible liquids). The page explains what is meant by an ideal mixture and looks at how the phase diagram for such a mixture is built up and used.
Ideal Mixtures
An ideal mixture is one which obeys Raoult's Law, but I want to look at the characteristics of an ideal mixture before actually stating Raoult's Law. The page will flow better if I do it this way around. There is actually no such thing as an ideal mixture! However, some liquid mixtures get fairly close to being ideal. These are mixtures of two very closely similar substances. Commonly quoted examples include:
- hexane and heptane
- benzene and methylbenzene
- propan-1-ol and propan-2-ol
In a pure liquid, some of the more energetic molecules have enough energy to overcome the intermolecular attractions and escape from the surface to form a vapor. The smaller the intermolecular forces, the more molecules will be able to escape at any particular temperature.

If you have a second liquid, the same thing is true. At any particular temperature a certain proportion of the molecules will have enough energy to leave the surface.
In an ideal mixture of these two liquids, the tendency of the two different sorts of molecules to escape is unchanged.
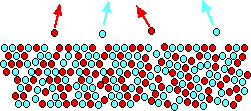
You might think that the diagram shows only half as many of each molecule escaping - but the proportion of each escaping is still the same. The diagram is for a 50/50 mixture of the two liquids. That means that there are only half as many of each sort of molecule on the surface as in the pure liquids. If the proportion of each escaping stays the same, obviously only half as many will escape in any given time. If the red molecules still have the same tendency to escape as before, that must mean that the intermolecular forces between two red molecules must be exactly the same as the intermolecular forces between a red and a blue molecule.
If the forces were any different, the tendency to escape would change. Exactly the same thing is true of the forces between two blue molecules and the forces between a blue and a red. They must also be the same otherwise the blue ones would have a different tendency to escape than before. If you follow the logic of this through, the intermolecular attractions between two red molecules, two blue molecules or a red and a blue molecule must all be exactly the same if the mixture is to be ideal.
This is why mixtures like hexane and heptane get close to ideal behavior. They are similarly sized molecules and so have similarly sized van der Waals attractions between them. However, they obviously are not identical - and so although they get close to being ideal, they are not actually ideal. For the purposes of this topic, getting close to ideal is good enough!
Ideal Mixtures and the Enthalpy of Mixing
When you make any mixture of liquids, you have to break the existing intermolecular attractions (which needs energy), and then remake new ones (which releases energy). If all these attractions are the same, there won't be any heat either evolved or absorbed. That means that an ideal mixture of two liquids will have zero enthalpy change of mixing. If the temperature rises or falls when you mix the two liquids, then the mixture is not ideal. You may have come cross a slightly simplified version of Raoult's Law if you have studied the effect of a non-volatile solute like salt on the vapor pressure of solvents like water. The definition below is the one to use if you are talking about mixtures of two volatile liquids.
Definition: Raoult's Law
The partial vapor pressure of a component in a mixture is equal to the vapor pressure of the pure component at that temperature multiplied by its mole fraction in the mixture.
Raoult's Law only works for ideal mixtures. In equation form, for a mixture of liquids \(A\) and \(B\), this reads:
\[ P_A = X_A P^*_A \label{1}\]
\[ P_B = X_B P^*_B \label{2}\]
In this equation, \(P_A\) and \(P_B\) are the partial vapor pressures of the components \(A\) and \(B\). In any mixture of gases, each gas exerts its own pressure. This is called its partial pressure and is independent of the other gases present. Even if you took all the other gases away, the remaining gas would still be exerting its own partial pressure. The total vapor pressure of the mixture is equal to the sum of the individual partial pressures:
\[ P_{\text{total}} = P_A + P_B \label{3}\]
The \(P^*\) values are the vapor pressures of \(A\) and \(B\) if they were on their own as pure liquids. \(X_A\) and \(X_B\) are the mole fractions of \(A\) and \(B\). That is exactly what it says it is - the fraction of the total number of moles present which is \(A\) or \(B\). You calculate mole fraction using, for example:
\[ X_A = \dfrac{\text{moles of A}}{\text{total number of moles}} \label{4}\]
Example \(\PageIndex{1}\)
Suppose you had a mixture of 2 moles of methanol and 1 mole of ethanol at a particular temperature. The vapor pressure of pure methanol at this temperature is 81 kPa, and the vapor pressure of pure ethanol is 45 kPa. What is total vapor pressure of this solution?
Solution
There are 3 moles in the mixture in total.
- 2 of these are methanol. The mole fraction of methanol is 2/3.
- Similarly, the mole fraction of ethanol is 1/3.
You can easily find the partial vapor pressures using Raoult's Law - assuming that a mixture of methanol and ethanol is ideal.
First for methanol:
\[ P_{methanol} = \dfrac{2}{3} \times 81\; kPa\]
\[ = 54\; kPa\]
Then for ethanol:
\[ P_{ethanol} = \dfrac{1}{3} \times 45\; kPa\]
\[ = 15\; kPa\]
You get the total vapor pressure of the liquid mixture by adding these together.
\[ P_{total} = 54\; kPa + 15 \; kPa = 69 kPa\]
In practice, this is all a lot easier than it looks when you first meet the definition of Raoult's Law and the equations!
Vapor Pressure and Composition Diagrams
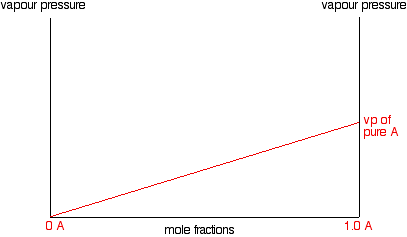
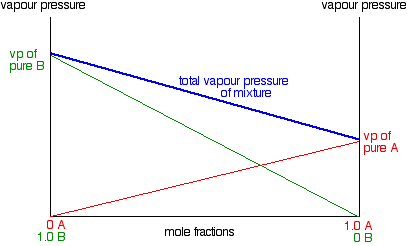
Suppose you have an ideal mixture of two liquids A and B. Each of A and B is making its own contribution to the overall vapor pressure of the mixture - as we've seen above. Let's focus on one of these liquids - A, for example. Suppose you double the mole fraction of A in the mixture (keeping the temperature constant). According to Raoult's Law, you will double its partial vapor pressure. If you triple the mole fraction, its partial vapor pressure will triple - and so on. In other words, the partial vapor pressure of A at a particular temperature is proportional to its mole fraction. If you plot a graph of the partial vapor pressure of A against its mole fraction, you will get a straight line.
Now we'll do the same thing for B - except that we will plot it on the same set of axes. The mole fraction of B falls as A increases so the line will slope down rather than up. As the mole fraction of B falls, its vapor pressure will fall at the same rate.
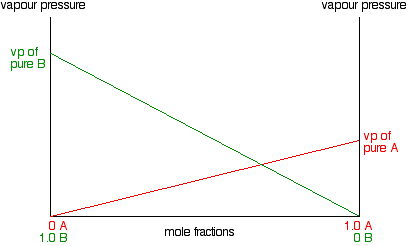
Notice that the vapor pressure of pure B is higher than that of pure A. That means that molecules must break away more easily from the surface of B than of A. B is the more volatile liquid. To get the total vapor pressure of the mixture, you need to add the values for A and B together at each composition. The net effect of that is to give you a straight line as shown in the next diagram.
Boiling point and Composition Diagrams
The relationship between boiling point and vapor pressure
- If a liquid has a high vapor pressure at a particular temperature, it means that its molecules are escaping easily from the surface.
- If, at the same temperature, a second liquid has a low vapor pressure, it means that its molecules are not escaping so easily.
What do these two aspects imply about the boiling points of the two liquids? There are two ways of looking at the above question:
Either:
-
If the molecules are escaping easily from the surface, it must mean that the intermolecular forces are relatively weak. That means that you won't have to supply so much heat to break them completely and boil the liquid. Therefore, the liquid with the higher vapor pressure at a particular temperature is the one with the lower boiling point.
Or:
-
Liquids boil when their vapor pressure becomes equal to the external pressure. If a liquid has a high vapor pressure at some temperature, you won't have to increase the temperature very much until the vapor pressure reaches the external pressure. On the other hand if the vapor pressure is low, you will have to heat it up a lot more to reach the external pressure. Therefore, the liquid with the higher vapor pressure at a particular temperature is the one with the lower boiling point.
For two liquids at the same temperature, the liquid with the higher vapor pressure is the one with the lower boiling point.
Constructing a boiling point / composition diagram
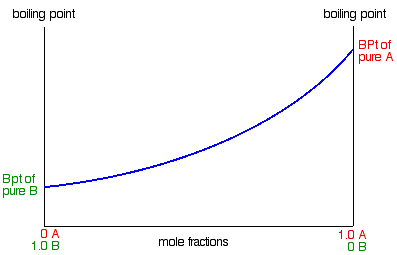
To remind you - we've just ended up with this vapor pressure / composition diagram:

We're going to convert this into a boiling point / composition diagram. We'll start with the boiling points of pure A and B. Since B has the higher vapor pressure, it will have the lower boiling point. If that is not obvious to you, go back and read the last section again!

For mixtures of A and B, you might perhaps have expected that their boiling points would form a straight line joining the two points we've already got. Not so! In fact, it turns out to be a curve.
To make this diagram really useful (and finally get to the phase diagram we've been heading towards), we are going to add another line. This second line will show the composition of the vapor over the top of any particular boiling liquid.
If you boil a liquid mixture, you would expect to find that the more volatile substance escapes to form a vapor more easily than the less volatile one. That means that in the case we've been talking about, you would expect to find a higher proportion of B (the more volatile component) in the vapor than in the liquid. You can discover this composition by condensing the vapor and analyzing it. That would give you a point on the diagram.
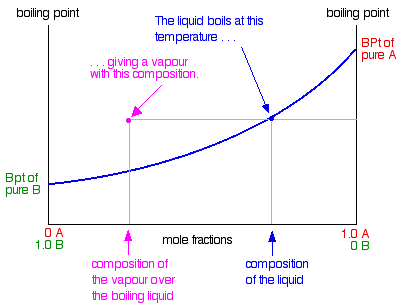
The diagram just shows what happens if you boil a particular mixture of A and B. Notice that the vapor over the top of the boiling liquid has a composition which is much richer in B - the more volatile component. If you repeat this exercise with liquid mixtures of lots of different compositions, you can plot a second curve - a vapor composition line.
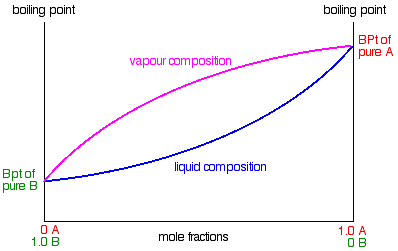
This is now our final phase diagram.
Using the phase diagram
The diagram is used in exactly the same way as it was built up. If you boil a liquid mixture, you can find out the temperature it boils at, and the composition of the vapor over the boiling liquid. For example, in the next diagram, if you boil a liquid mixture C1, it will boil at a temperature T1 and the vapor over the top of the boiling liquid will have the composition C2.
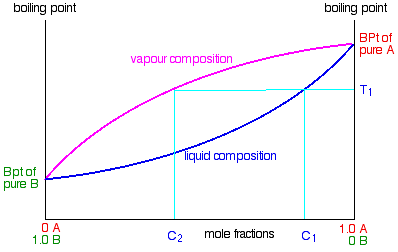
All you have to do is to use the liquid composition curve to find the boiling point of the liquid, and then look at what the vapor composition would be at that temperature. Notice again that the vapor is much richer in the more volatile component B than the original liquid mixture was.
The beginnings of fractional distillation
Suppose that you collected and condensed the vapor over the top of the boiling liquid and reboiled it. You would now be boiling a new liquid which had a composition C2. That would boil at a new temperature T2, and the vapor over the top of it would have a composition C3.
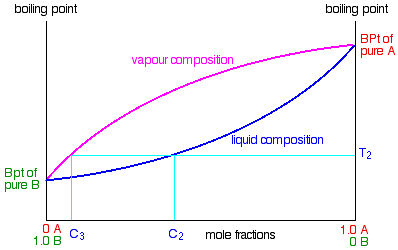
You can see that we now have a vapor which is getting quite close to being pure B. If you keep on doing this (condensing the vapor, and then reboiling the liquid produced) you will eventually get pure B. This is obvious the basis for fractional distillation. However, doing it like this would be incredibly tedious, and unless you could arrange to produce and condense huge amounts of vapor over the top of the boiling liquid, the amount of B which you would get at the end would be very small. Real fractionating columns (whether in the lab or in industry) automate this condensing and reboiling process. How these work will be explored on another page.
Contributors
Jim Clark (Chemguide.co.uk)


